0.003 Is 1 10 Of
cibeltiagestion
Sep 08, 2025 · 5 min read
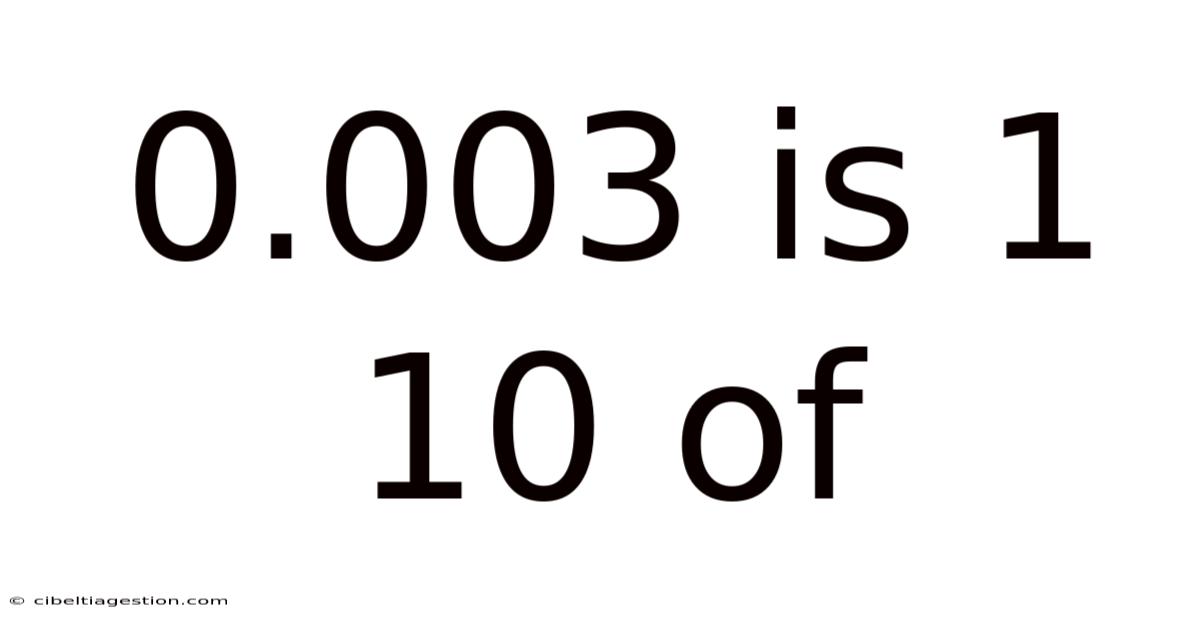
Table of Contents
Decoding 0.003: Understanding its Relationship to 1/1000
The statement "0.003 is 1/1000 of" is incomplete; it needs a reference point to be meaningful. This article will delve into the intricacies of understanding decimal numbers, specifically 0.003, and explain its relationship to fractions, particularly 1/1000, and how it relates to various quantities. We'll explore its practical applications and clear up any potential confusion surrounding decimal representation and fraction equivalents. This will provide a comprehensive understanding of decimal numbers and their fractional counterparts.
Understanding Decimal Numbers
Decimal numbers are a way of representing numbers using a base-10 system. This means that each digit's position relative to the decimal point determines its value. The digits to the left of the decimal point represent whole numbers, while the digits to the right represent fractions of a whole. Each position to the right of the decimal point represents a successively smaller fraction of 1.
- The first digit after the decimal point represents tenths (1/10).
- The second digit represents hundredths (1/100).
- The third digit represents thousandths (1/1000).
- And so on...
Therefore, the number 0.003 represents three thousandths. This is because the '3' is in the thousandths place. We can express this mathematically as 3/1000.
0.003 as a Fraction: The Equivalence to 1/1000 and Beyond
As established, 0.003 is equivalent to the fraction 3/1000. This is a direct representation of the decimal value. Now, to address the incomplete statement "0.003 is 1/1000 of...", we need to specify what 0.003 is a fraction of.
-
0.003 is 3/1000 of 1. This is the simplest and most direct answer. It directly reflects the value of 0.003 as a fraction of the whole number 1.
-
0.003 is 1/1000 of 3. This is another valid interpretation. If we consider the fraction 1/1000, multiplying it by 3 gives us 3/1000, which is equivalent to 0.003.
-
0.003 is 1/1000 of any number X, where X = 3. This generalizes the concept. We can choose any number (X) and say 0.003 represents 1/1000th of that number, provided X is equal to 3. This is because 0.003 * 1000 = 3.
Practical Applications of Understanding 0.003
Understanding the concept of 0.003 and its fractional equivalent has numerous applications across various fields:
-
Science and Engineering: In scientific measurements, 0.003 might represent a small change in a physical quantity such as a temperature difference, a minute change in length, or a slight variation in pressure. The ability to represent and interpret such small values is crucial for precision and accuracy.
-
Finance and Economics: In financial markets, 0.003 could represent a small percentage change in the value of an asset. For example, a 0.003 increase in the interest rate might seem insignificant, but when dealing with large sums of money, it can translate to substantial monetary gains or losses.
-
Computer Science: In computer programming and data analysis, 0.003 might represent a small probability or a fractional value within a larger dataset. The ability to handle decimal values is critical for accurate calculations and simulations.
-
Manufacturing and Engineering Tolerances: In manufacturing, tolerance levels often use decimal values. A tolerance of ±0.003 inches means that a dimension can vary by a maximum of 0.003 inches above or below the specified value. Precision manufacturing necessitates understanding these small variations.
-
Everyday Life: While less obvious, we encounter decimal values like 0.003 in everyday contexts. For instance, measuring small amounts of ingredients in cooking or calculating the exact cost of an item with sales tax can involve working with decimal fractions.
Understanding Decimal to Fraction Conversion
Converting decimals to fractions is a fundamental skill in mathematics. The process involves:
-
Identify the place value of the last digit: In 0.003, the last digit (3) is in the thousandths place.
-
Write the decimal as a fraction: The denominator will be the place value (1000 in this case), and the numerator will be the digits to the right of the decimal point (3). This gives us 3/1000.
-
Simplify the fraction (if possible): In this case, 3/1000 is already in its simplest form because 3 and 1000 have no common factors other than 1.
Further Exploring Decimal and Fractional Relationships
Beyond the simple conversion of 0.003, we can explore its relationships with other decimals and fractions:
-
Comparing Decimals: 0.003 is smaller than 0.01, 0.1, and 1. It’s important to understand the relative sizes of decimal numbers.
-
Adding and Subtracting Decimals: Adding or subtracting decimals requires aligning the decimal points. For example, 0.003 + 0.007 = 0.010.
-
Multiplying and Dividing Decimals: Multiplying and dividing decimals requires careful attention to decimal place values. For instance, 0.003 x 1000 = 3, and 0.003 ÷ 3 = 0.001.
Frequently Asked Questions (FAQ)
Q: What is the difference between 0.003 and 0.03?
A: The difference lies in the place value of the digit 3. In 0.003, the 3 is in the thousandths place, representing 3/1000. In 0.03, the 3 is in the hundredths place, representing 3/100. Therefore, 0.03 is ten times larger than 0.003.
Q: How do I convert 0.003 into a percentage?
A: To convert a decimal to a percentage, multiply it by 100. 0.003 x 100 = 0.3%, meaning 0.003 represents 0.3% of 1.
Q: Can 0.003 be expressed as a percentage of a larger number?
A: Yes. To express 0.003 as a percentage of any number X, you calculate (0.003/X) * 100%. For example, if X = 1000, then (0.003/1000) * 100% = 0.03%.
Conclusion: Mastering the Nuances of 0.003
Understanding the value of 0.003, its fractional representation (3/1000), and its relationship to 1/1000 is crucial for various applications, from precise scientific measurements to financial calculations. This article has provided a detailed explanation, bridging the gap between decimal representation and fractional understanding. By grasping these fundamental concepts, individuals can confidently tackle more complex mathematical problems involving decimals and fractions, fostering a stronger foundation in numerical literacy. Remember, the key is to understand the place value of each digit and how it contributes to the overall value of the number. This understanding empowers you to handle numbers effectively and solve various real-world problems.
Latest Posts
Latest Posts
-
750 Ml To Fl Ounces
Sep 09, 2025
-
Fe No2 3 Compound Name
Sep 09, 2025
-
Alcohol Withdrawal Seizure Icd 10
Sep 09, 2025
-
Is Hclo4 A Strong Acid
Sep 09, 2025
-
12 More Than M Machines
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 0.003 Is 1 10 Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.