0.08 Is 1 10 Of
cibeltiagestion
Sep 01, 2025 · 5 min read
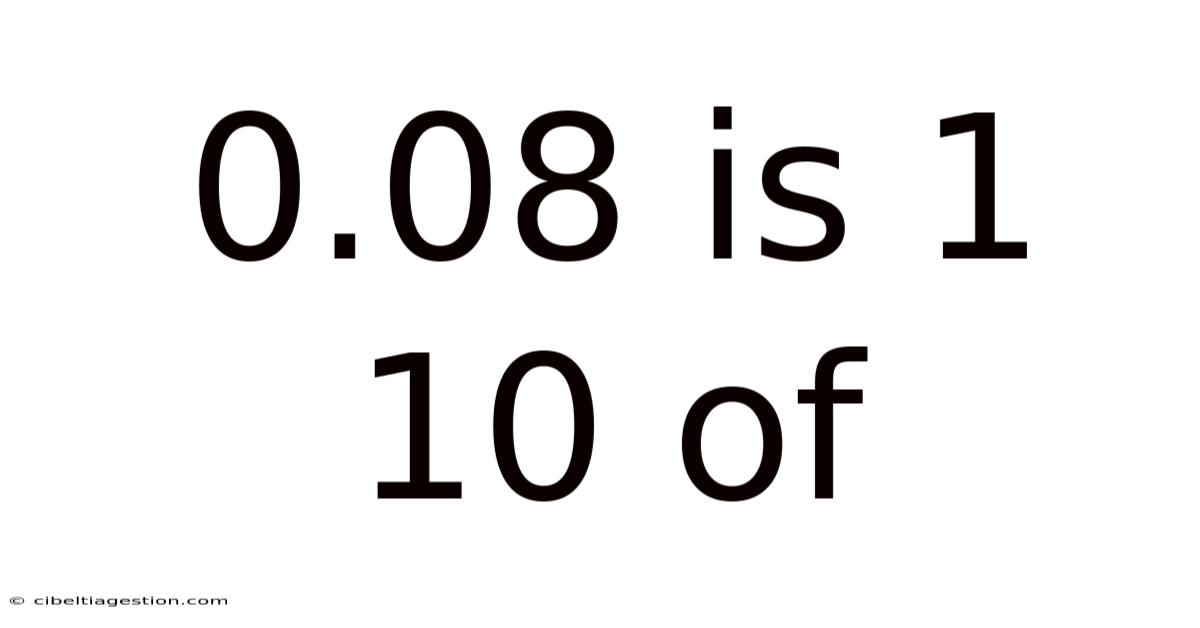
Table of Contents
Decoding 0.08: Understanding its Relationship to 1/10 and Fractions
The statement "0.08 is 1/10 of..." is incomplete, and understanding why requires a solid grasp of decimals, fractions, and their interrelationship. This article will not only clarify the relationship between 0.08 and 1/10 but also delve deeper into the fundamental concepts, equipping you with a comprehensive understanding of decimal and fractional representation. We'll explore various methods for solving this type of problem and uncover the underlying mathematical principles.
Introduction: Decimals, Fractions, and their Interplay
Decimals and fractions are two different ways of representing the same thing: parts of a whole. A decimal uses a base-10 system, with a decimal point separating the whole number from the fractional part. A fraction, on the other hand, represents a part of a whole using a numerator (top number) and a denominator (bottom number). The denominator indicates the total number of equal parts, and the numerator shows how many of those parts are being considered.
Understanding the relationship between decimals and fractions is crucial for solving mathematical problems. Converting between these two forms is a fundamental skill that opens doors to more complex mathematical concepts.
Understanding the Problem: "0.08 is 1/10 of..."
The statement "0.08 is 1/10 of..." implies a proportional relationship. We know that 0.08 represents a certain part of a whole. The fraction 1/10 represents one-tenth of that whole. The question asks us to find the whole number which, when multiplied by 1/10, results in 0.08.
To solve this, we need to apply the concept of inverse operations. Since 1/10 is multiplied by the unknown number to get 0.08, we need to perform the inverse operation of multiplication: division.
Step-by-Step Solution: Finding the Whole Number
-
Convert the fraction to a decimal: 1/10 is equivalent to 0.1 (one divided by ten equals 0.1).
-
Set up an equation: We can represent the problem as an equation: 0.1 * x = 0.08, where 'x' is the unknown whole number we need to find.
-
Solve for x: To isolate 'x', divide both sides of the equation by 0.1:
x = 0.08 / 0.1
-
Perform the division: Dividing 0.08 by 0.1 gives us:
x = 0.8
Therefore, 0.08 is 1/10 of 0.8.
Alternative Solution: Using Fractions
We can also solve this problem using fractions throughout the process.
-
Convert the decimal to a fraction: 0.08 can be written as 8/100 (8 hundredths). This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 4: 8/100 simplifies to 2/25.
-
Set up an equation using fractions: The problem can be represented as: (1/10) * x = (2/25)
-
Solve for x: To isolate 'x', multiply both sides of the equation by the reciprocal of 1/10, which is 10/1 (or simply 10):
x = (2/25) * (10/1)
-
Perform the multiplication: Multiply the numerators together and the denominators together:
x = 20/25
-
Simplify the fraction: Divide both the numerator and the denominator by their greatest common divisor, which is 5:
x = 4/5
-
Convert the fraction back to a decimal: 4/5 is equivalent to 0.8
Again, we arrive at the same answer: 0.08 is 1/10 of 0.8.
Scientific Explanation: Proportional Relationships
The core concept behind this problem is a proportional relationship. Proportionality means that two quantities are related in such a way that when one changes, the other changes in a consistent manner. In this case, 0.08 is proportionally related to an unknown number (x) through the factor 1/10.
This proportional relationship can be expressed using the following formula:
y = kx
Where:
- y is the dependent variable (0.08 in our case)
- x is the independent variable (the unknown number we're looking for)
- k is the constant of proportionality (1/10 in our case)
By understanding this relationship, we can solve various proportional problems by manipulating this formula.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to solve this problem?
A1: Absolutely! Calculators are excellent tools for performing decimal calculations. You can directly input 0.08 / 0.1 or use the fraction functionality to perform the calculation with fractions.
Q2: What if the fraction was different? For example, what if it was 1/5?
A2: The method remains the same. You would replace 1/10 with 1/5 (or its decimal equivalent, 0.2) in the equation and solve for x accordingly.
Q3: Why is it important to understand the relationship between decimals and fractions?
A3: Understanding the relationship between decimals and fractions is fundamental to various mathematical applications. It improves problem-solving skills, enables easier conversions between different numerical representations, and forms the base for understanding more complex concepts such as percentages, ratios, and proportions.
Q4: Are there any real-world applications of this type of problem?
A4: Yes! Proportional relationships are prevalent in various real-world scenarios, including:
- Scaling recipes: If a recipe calls for a certain amount of an ingredient, and you want to make a smaller or larger batch, you’ll use proportional relationships.
- Calculating discounts: Sales and discounts are often expressed as percentages or fractions, requiring proportional calculations.
- Measuring distances on maps: Maps use scales which are proportional relationships between map distances and real-world distances.
- Determining speeds and distances: Calculating travel times and distances requires understanding proportional relationships between speed, time, and distance.
Conclusion: Mastering Decimals and Fractions
This article explored the problem "0.08 is 1/10 of..." demonstrating two distinct yet equally valid approaches: using decimals and using fractions. We uncovered that 0.08 is 1/10 of 0.8, highlighting the importance of understanding proportional relationships. By mastering the conversion between decimals and fractions and applying the concepts of inverse operations and proportional relationships, you'll be well-equipped to tackle similar problems and enhance your overall mathematical understanding. Remember, the key is to break down the problem into manageable steps, choose the method you find most comfortable, and practice regularly to build confidence and proficiency. The ability to seamlessly move between decimals and fractions is a valuable tool in your mathematical arsenal.
Latest Posts
Latest Posts
-
When Are The Nucleoli Visible
Sep 02, 2025
-
How Far Is 3000 M
Sep 02, 2025
-
Local Health Codes Establish Requirements
Sep 02, 2025
-
78 Kg In Us Pounds
Sep 02, 2025
-
Convert 37 6 Celsius To Fahrenheit
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about 0.08 Is 1 10 Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.