0.1 X 0.2 X 2
cibeltiagestion
Sep 01, 2025 · 5 min read
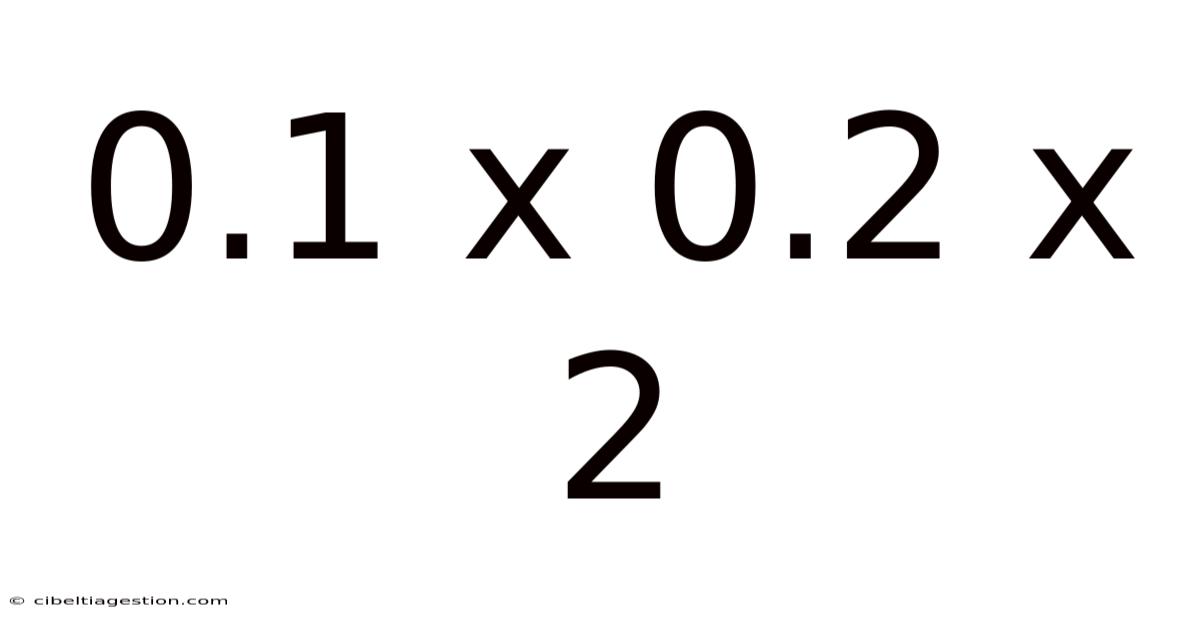
Table of Contents
Decoding 0.1 x 0.2 x 2: A Deep Dive into Decimal Multiplication and its Applications
This article explores the seemingly simple mathematical expression, 0.1 x 0.2 x 2, going beyond a straightforward calculation to delve into the underlying principles of decimal multiplication, its practical applications, and the broader context of mathematical operations. Understanding this basic calculation lays the foundation for more complex mathematical concepts and real-world problem-solving.
Introduction: Understanding Decimal Numbers and Multiplication
Before tackling the specific calculation, let's refresh our understanding of decimals and multiplication. Decimal numbers are numbers that include a fractional part, separated from the whole number part by a decimal point (.). Each digit to the right of the decimal point represents a progressively smaller fraction of one (tenths, hundredths, thousandths, and so on). Multiplication, on the other hand, is a fundamental arithmetic operation representing repeated addition or scaling. When multiplying decimal numbers, the principles remain the same, but we must carefully handle the placement of the decimal point in the final result.
Step-by-Step Calculation: 0.1 x 0.2 x 2
The calculation 0.1 x 0.2 x 2 can be solved step-by-step, following the order of operations (multiplication from left to right):
-
0.1 x 0.2: First, we multiply 0.1 and 0.2. Ignoring the decimal points for now, we multiply 1 x 2 = 2. Since there is a total of two decimal places in the original numbers (one in 0.1 and one in 0.2), we place the decimal point two places from the right in the result, giving us 0.02.
-
0.02 x 2: Next, we multiply the result (0.02) by 2. Again, ignoring the decimal point initially, we have 2 x 2 = 4. There are two decimal places in 0.02, so we place the decimal point two places from the right in the final answer, giving us 0.04.
Therefore, 0.1 x 0.2 x 2 = 0.04.
Explanation: The Significance of Decimal Place Value
The seemingly simple act of placing the decimal point is crucial. It directly reflects the value of each digit in the decimal number system. When multiplying decimals, the number of decimal places in the result is the sum of the decimal places in the numbers being multiplied. This is why we moved the decimal point two places to the left in both steps of the calculation. Failing to accurately manage decimal places leads to incorrect answers, highlighting the importance of understanding place value.
Illustrative Examples: Real-World Applications of Decimal Multiplication
Decimal multiplication is ubiquitous in various aspects of daily life and specialized fields. Here are a few examples showcasing the practical application of similar calculations:
-
Finance: Calculating discounts, interest, taxes, and profits often involves decimal multiplication. For instance, a 10% discount (0.1) on a $20 item (20) would be calculated as 0.1 x 20 = $2. Similarly, calculating compound interest requires repeated decimal multiplications.
-
Engineering and Physics: In fields like engineering and physics, calculations involving dimensions, forces, and material properties frequently use decimal numbers. Determining the volume of a rectangular prism with dimensions of 0.1 meters, 0.2 meters, and 2 meters would be a direct application of the 0.1 x 0.2 x 2 calculation, resulting in a volume of 0.04 cubic meters.
-
Chemistry: In chemistry, molarity (concentration of a solution) is often expressed using decimal numbers. Calculations involving dilutions and stoichiometry rely heavily on decimal multiplication.
-
Computer Science: In computer graphics and image processing, decimal numbers represent pixel coordinates and color values. Manipulating these values through multiplication is crucial for scaling images, applying filters, and other image processing tasks.
Expanding the Concept: Beyond 0.1 x 0.2 x 2
The calculation 0.1 x 0.2 x 2 serves as a basic building block for more complex problems. Consider these extensions:
-
Larger Decimal Numbers: The same principles apply when multiplying larger decimal numbers. For instance, 3.14 x 2.71 x 0.5 involves the same fundamental process, albeit with a greater number of decimal places to manage in the final answer.
-
Scientific Notation: For extremely large or small numbers, scientific notation (using powers of 10) becomes essential. This simplifies calculations and improves readability. For example, 1.2 x 10^3 multiplied by 5.0 x 10^-2 is a prime example where understanding decimals and exponents are both necessary.
-
Algebraic Expressions: Decimal multiplication is integrated into algebraic expressions, equations, and formulas. Solving for unknowns often involves manipulating decimal numbers within a broader mathematical context.
Frequently Asked Questions (FAQ)
-
Q: What if the order of multiplication is changed?
- A: The commutative property of multiplication states that the order of the numbers does not affect the result. Thus, 0.1 x 2 x 0.2 will still equal 0.04.
-
Q: Can I use a calculator for this calculation?
- A: Yes, calculators are valuable tools for efficient calculations, particularly with more complex decimal multiplications. However, understanding the underlying principles remains crucial for problem-solving and error detection.
-
Q: What happens if I make a mistake in placing the decimal point?
- A: Incorrect placement of the decimal point will lead to an incorrect answer, possibly by orders of magnitude. This underscores the importance of careful calculation and double-checking your work.
-
Q: How can I improve my decimal multiplication skills?
- A: Practice is key. Work through various problems, starting with simple examples like 0.1 x 0.2 x 2 and gradually increasing the complexity. Familiarize yourself with place value and the rules for multiplying decimals.
Conclusion: Mastering Decimal Multiplication for Future Success
The seemingly insignificant calculation of 0.1 x 0.2 x 2 reveals fundamental principles of decimal multiplication applicable across diverse fields. Mastering these principles is crucial for success not only in mathematics but also in various real-world applications. From finance to engineering to computer science, understanding how to accurately multiply decimal numbers ensures accurate calculations and problem-solving, laying a solid foundation for more advanced mathematical concepts and future endeavors. The focus should not just be on arriving at the answer (0.04), but understanding why and how that answer is derived, ensuring a deep and lasting comprehension of this crucial mathematical concept. This understanding fosters a more intuitive and confident approach to more complex mathematical challenges.
Latest Posts
Latest Posts
-
Can A Pca Give Insulin
Sep 01, 2025
-
1 6 Repeating As A Fraction
Sep 01, 2025
-
Demizion Valley Orchard Inc Devleoped
Sep 01, 2025
-
The Higher The Speed The
Sep 01, 2025
-
Biological Evolution Evidence Quick Check
Sep 01, 2025
Related Post
Thank you for visiting our website which covers about 0.1 X 0.2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.