0.3 Repeated As A Fraction
cibeltiagestion
Sep 13, 2025 · 6 min read
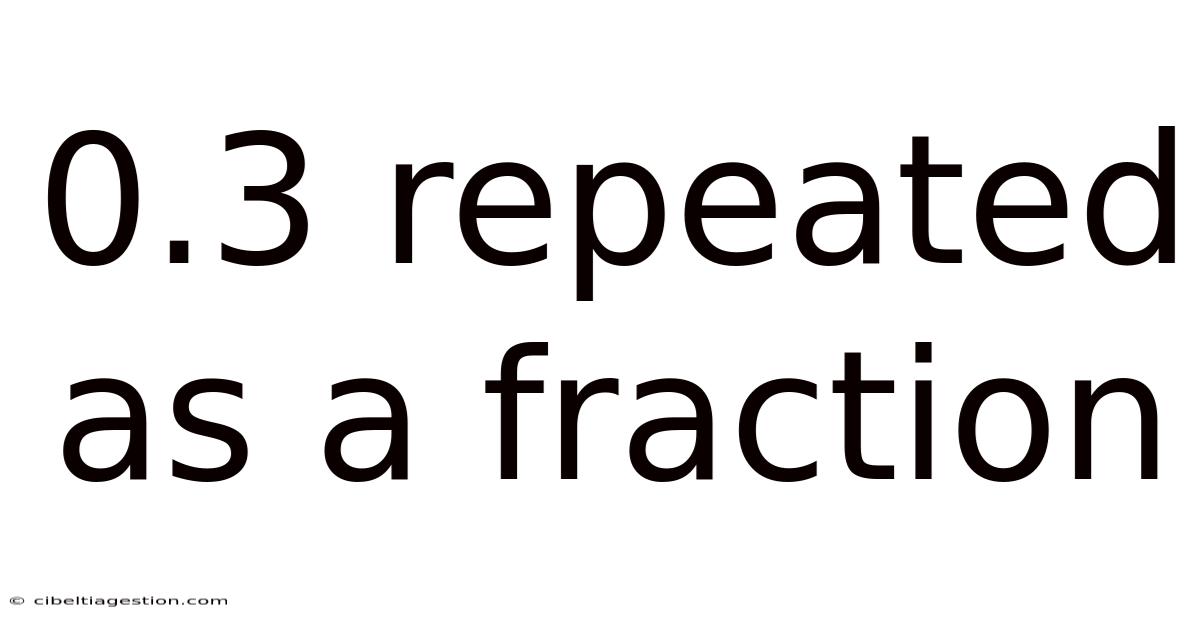
Table of Contents
Decoding 0.333... : Understanding Repeating Decimals and their Fractional Equivalents
Have you ever wondered how to represent the seemingly endless decimal 0.333... as a fraction? This seemingly simple question opens a door to a deeper understanding of the relationship between decimals and fractions, a fundamental concept in mathematics. This article will guide you through the process of converting repeating decimals, specifically 0.333..., into its fractional form, exploring the underlying mathematical principles and offering practical applications. We'll cover various methods, delve into the mathematical reasoning, and address frequently asked questions to ensure a comprehensive understanding.
Understanding Repeating Decimals
Before diving into the conversion process, let's clarify what a repeating decimal is. A repeating decimal, also known as a recurring decimal, is a decimal number that has a digit or a group of digits that repeat infinitely. The repeating part is usually indicated by a bar placed above the repeating digits. For example, 0.333... is written as 0.$\overline{3}$, indicating that the digit 3 repeats indefinitely. Other examples include 0.142857142857..., which can be written as 0.$\overline{142857}$, and 0.666..., or 0.$\overline{6}$.
Method 1: The Algebraic Approach – Solving for x
This is a classic and elegant method for converting repeating decimals to fractions. Let's apply it to 0.333...
1. Set up an equation:
Let x = 0.333...
2. Multiply to shift the decimal:
Multiply both sides of the equation by 10 (or a power of 10 depending on the number of repeating digits):
10x = 3.333...
3. Subtract the original equation:
Subtract the original equation (x = 0.333...) from the equation obtained in step 2:
10x - x = 3.333... - 0.333...
This simplifies to:
9x = 3
4. Solve for x:
Divide both sides by 9:
x = 3/9
5. Simplify the fraction:
Simplify the fraction to its lowest terms:
x = 1/3
Therefore, 0.333... is equal to 1/3.
Method 2: The Geometric Series Approach
This method utilizes the concept of an infinite geometric series. An infinite geometric series is a sum of an infinite number of terms where each term is obtained by multiplying the previous term by a constant value (the common ratio). The sum of an infinite geometric series converges to a finite value if the absolute value of the common ratio is less than 1.
We can express 0.333... as the sum of an infinite geometric series:
0.3 + 0.03 + 0.003 + 0.0003 + ...
In this series:
- The first term (a) is 0.3
- The common ratio (r) is 0.1
The formula for the sum of an infinite geometric series is:
Sum = a / (1 - r)
Substituting the values from our series:
Sum = 0.3 / (1 - 0.1) = 0.3 / 0.9 = 3/9 = 1/3
Method 3: Understanding Place Value
This method emphasizes the fundamental concept of place value in decimal numbers. 0.333... can be expressed as:
3/10 + 3/100 + 3/1000 + 3/10000 + ...
This is an infinite series. While we cannot directly sum an infinite number of terms, we can use the formula for the sum of an infinite geometric series (as shown in Method 2) or recognize this as a convergent series that approaches a limit. This limit, as we've already demonstrated, is 1/3.
This method helps visualize the contribution of each digit to the overall value and reinforces the relationship between decimal representation and the fractional components.
Why Does This Work? The Mathematical Rationale
The success of these methods hinges on the properties of infinite geometric series and the manipulation of equations. The key is recognizing that the repeating decimal represents an infinite sum, which, under certain conditions (like the common ratio being less than 1 in absolute value), converges to a finite value – a rational number representable as a fraction. The algebraic method cleverly uses multiplication and subtraction to isolate and solve for the repeating decimal, transforming it into a manageable equation solvable for a fractional representation.
Expanding the Concept: Converting Other Repeating Decimals
The methods outlined above can be generalized to convert any repeating decimal into a fraction. Let's consider another example: 0.666...
Using the algebraic method:
- Let x = 0.666...
- 10x = 6.666...
- 10x - x = 6.666... - 0.666...
- 9x = 6
- x = 6/9 = 2/3
Therefore, 0.666... = 2/3.
For repeating decimals with more than one repeating digit, you'll need to multiply by a higher power of 10 (e.g., 100 for two repeating digits, 1000 for three, etc.) to align the decimal points effectively before subtracting the original equation. The core principle remains the same: manipulate the equation to isolate the repeating part and convert it to a fraction.
Practical Applications
Understanding the conversion of repeating decimals to fractions is not merely an academic exercise. It has applications in various fields:
- Computer science: Representing numbers in binary and other number systems often involves working with fractions and repeating decimals.
- Engineering: Precision calculations in engineering frequently require the use of fractions for accuracy.
- Finance: Calculations involving percentages and interest rates sometimes result in repeating decimals that need to be converted to fractions for precise calculations.
- Physics: Many physical constants are expressed as fractions or irrational numbers with decimal approximations that may be repeating.
Frequently Asked Questions (FAQ)
Q1: Can all repeating decimals be expressed as fractions?
A1: Yes, all repeating decimals can be expressed as fractions (rational numbers). This is a fundamental property of rational numbers. Non-repeating decimals, on the other hand, are typically irrational numbers (like π or √2) and cannot be exactly represented as fractions.
Q2: What if the repeating decimal starts after some non-repeating digits?
A2: For decimals with a non-repeating part followed by a repeating part, you can still use the algebraic method. You need to adjust the multiplication factor accordingly to align the repeating parts before subtraction. For example, for a number like 1.2$\overline{3}$, you would first isolate the repeating part (0.$\overline{3}$) by subtracting 1.2 and then proceed with the algebraic method.
Q3: Are there limitations to the algebraic method?
A3: While effective, the algebraic method can become cumbersome with extremely long repeating sequences. In such cases, computational methods or software might be more practical.
Q4: Why is understanding this concept important?
A4: This understanding is crucial for developing a solid foundation in mathematics. It strengthens your understanding of number systems, demonstrates the interplay between different mathematical representations, and equips you with a skill valuable in various fields.
Conclusion
Converting the repeating decimal 0.333... (or 0.$\overline{3}$) to its fractional equivalent, 1/3, is a testament to the elegance and interconnectedness of mathematical concepts. This seemingly simple conversion reveals profound truths about number systems and lays the groundwork for understanding more complex mathematical ideas. By understanding the underlying principles and applying the methods outlined above, you can confidently tackle the conversion of any repeating decimal into its fractional form, strengthening your mathematical skills and appreciation for the beauty and logic of mathematics. Remember, the key is to approach these problems systematically, focusing on the core principles of place value and the properties of infinite geometric series. With practice, these conversions will become second nature.
Latest Posts
Latest Posts
-
6 X 1 6x 1
Sep 13, 2025
-
59 Degrees F To C
Sep 13, 2025
-
3s 4s 3 4 Dimethylheptane
Sep 13, 2025
-
Atlanta Georgia Latitude And Longitude
Sep 13, 2025
-
84 Degrees F To C
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 0.3 Repeated As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.