1 1/5 As A Decimal
cibeltiagestion
Sep 12, 2025 · 6 min read
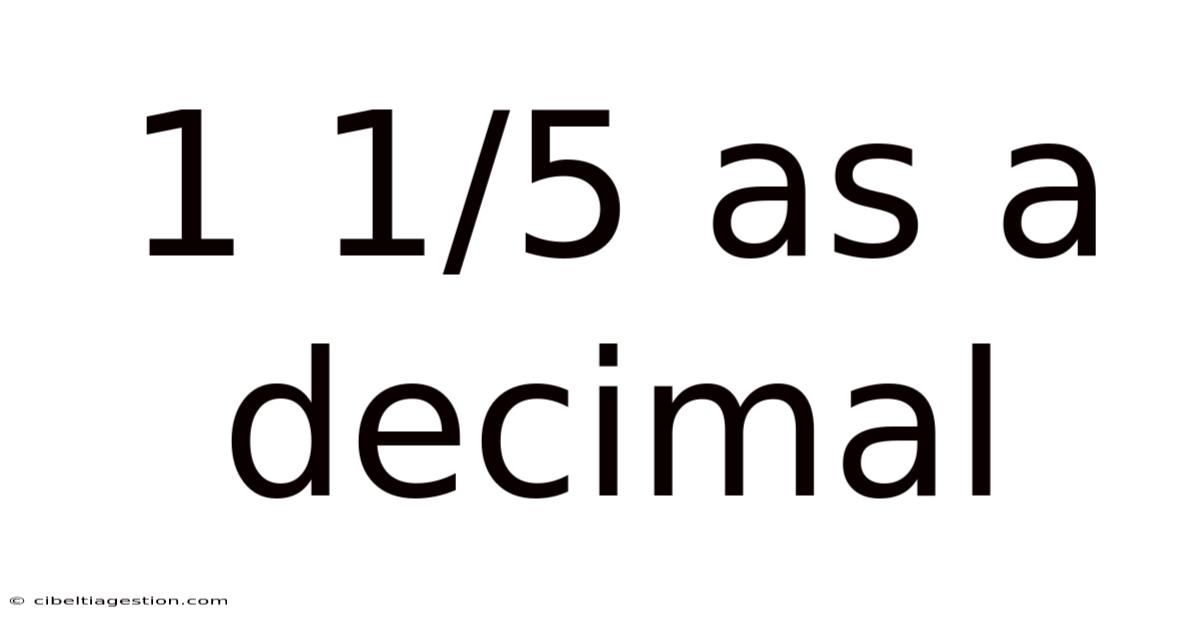
Table of Contents
1 1/5 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 1 1/5 into its decimal equivalent, exploring various methods and delving into the underlying principles. We'll cover not only the mechanics of the conversion but also provide practical applications and address frequently asked questions. By the end, you'll not only know the answer but also possess a deeper understanding of fractional and decimal representation.
Understanding Mixed Numbers and Fractions
Before we begin the conversion, let's refresh our understanding of mixed numbers and fractions. A mixed number combines a whole number and a fraction, such as 1 1/5. This represents one whole unit plus one-fifth of another unit. A fraction, on the other hand, represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In 1/5, 1 is the numerator and 5 is the denominator.
Method 1: Converting the Mixed Number to an Improper Fraction
The first and arguably most straightforward method involves converting the mixed number 1 1/5 into an improper fraction. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
- Multiply the whole number by the denominator: 1 * 5 = 5
- Add the numerator to the result: 5 + 1 = 6
- Keep the same denominator: The denominator remains 5.
Therefore, 1 1/5 is equivalent to the improper fraction 6/5.
Method 2: Direct Division
Once we have the improper fraction 6/5, we can easily convert it to a decimal by performing simple division. Remember that a fraction represents a division problem: the numerator divided by the denominator.
- Divide the numerator by the denominator: 6 ÷ 5 = 1.2
Therefore, 1 1/5 as a decimal is 1.2.
Method 3: Converting the Fractional Part Separately
Another approach involves converting the fractional part (1/5) to a decimal separately and then adding it to the whole number.
- Divide the numerator by the denominator: 1 ÷ 5 = 0.2
- Add the whole number: 1 + 0.2 = 1.2
This method reinforces the understanding that the mixed number represents a sum of a whole number and a fractional part.
Understanding the Decimal Representation
The decimal representation 1.2 signifies one whole unit and two-tenths of another unit. The digit to the left of the decimal point represents the whole number, while the digits to the right represent the fractional part. Each position to the right of the decimal point represents a decreasing power of 10: tenths, hundredths, thousandths, and so on. In 1.2, the '2' is in the tenths place, meaning it represents 2/10.
Practical Applications
The ability to convert fractions to decimals is essential in various real-world scenarios:
- Financial calculations: Working with percentages, interest rates, and monetary values often requires converting fractions to decimals for accurate computations. For instance, calculating a 1/5 discount on a price requires converting 1/5 to 0.2.
- Measurements: Many measuring systems use decimal representations, and converting fractions to decimals is crucial for accurate measurements and calculations. For example, converting inches to centimeters might involve working with fractions and decimals.
- Scientific calculations: In many scientific fields, decimals are commonly used for representing data and conducting calculations. Converting fractions to decimals is a necessary step in many scientific computations.
- Data analysis: Data analysis frequently involves working with numerical data, often requiring converting fractions into decimals for easier interpretation and analysis using software or spreadsheets.
- Everyday life: From recipes requiring fractional measurements to calculating fuel efficiency or splitting bills, converting fractions to decimals can simplify many everyday tasks.
Further Exploration: Different Fractions and Decimals
While we focused on 1 1/5, understanding the broader concept of fraction-to-decimal conversion is important. Let's consider some examples:
-
Terminating Decimals: Fractions with denominators that are factors of powers of 10 (e.g., 2, 5, 10, 20, 25, 50, 100) will always result in terminating decimals—decimals that end after a finite number of digits. For example, 1/4 = 0.25, and 3/10 = 0.3.
-
Repeating Decimals: Fractions with denominators that are not factors of powers of 10 often result in repeating decimals – decimals that have a sequence of digits that repeats infinitely. For example, 1/3 = 0.333... (the 3 repeats infinitely), and 1/7 has a repeating decimal expansion. These are often represented with a bar over the repeating sequence, such as 0.3̅
-
Converting Fractions with Larger Numerators and Denominators: The same principles apply to fractions with larger numbers. You can convert them to improper fractions first and then divide to obtain the decimal representation. For instance, to convert 3 2/7 to a decimal, first convert it to an improper fraction (23/7), and then divide 23 by 7.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 1 1/5 to a decimal?
A: Yes, absolutely! Most calculators have the capability to perform this conversion directly. You can either enter the fraction 6/5 or perform the division 6 ÷ 5 to get the decimal answer.
Q: What if the fraction is negative?
A: If the mixed number or fraction is negative (e.g., -1 1/5), perform the conversion as shown above, and then simply add the negative sign to the final result (-1.2).
Q: Are there other ways to convert fractions to decimals?
A: Yes. You could also use long division to manually divide the numerator by the denominator. This method is particularly helpful for understanding the underlying process and for handling fractions that don't convert to simple decimals.
Q: Why is understanding this conversion important?
A: Converting between fractions and decimals is crucial for various mathematical operations and real-world applications. It allows for seamless transitions between different forms of representing numerical values, leading to a more comprehensive understanding of numbers.
Conclusion
Converting 1 1/5 to a decimal is a simple yet fundamental mathematical operation with far-reaching applications. By understanding the different methods – converting to an improper fraction and then dividing, or converting the fractional part separately – you can confidently tackle this and similar conversions. This skill is essential for various disciplines, from finance and science to everyday life, making it a valuable asset in your mathematical toolkit. Remember the key is understanding the underlying principle of what a fraction represents: a division problem. Mastering this conversion strengthens your foundation in arithmetic and prepares you for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
21 Is 70 Of What
Sep 12, 2025
-
1 2 Cup To Ounces
Sep 12, 2025
-
10 Characteristics Of A Civilization
Sep 12, 2025
-
Dui Punishments Are Mostly About
Sep 12, 2025
-
How Many Ounces Is 30g
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 1/5 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.