1 12 Divided By 3
cibeltiagestion
Sep 16, 2025 · 6 min read
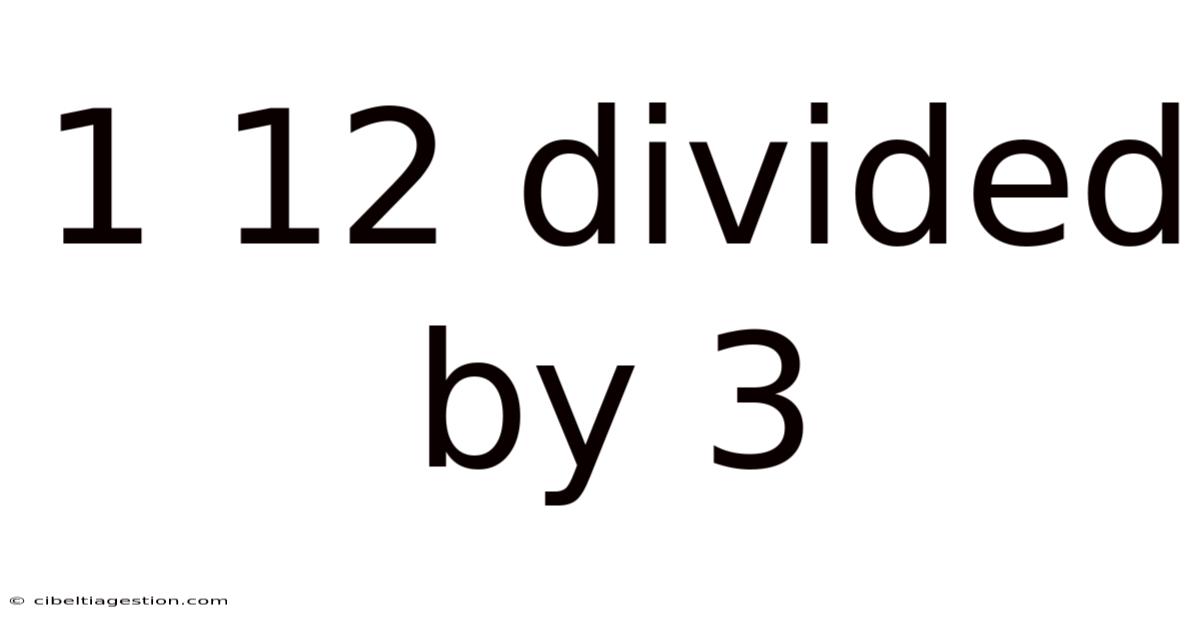
Table of Contents
1112 Divided by 3: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 1112 divided by 3, delving far beyond the basic arithmetic to uncover the underlying principles of division, its various applications in different fields, and the broader mathematical concepts it connects to. Understanding this single division problem allows us to grasp fundamental concepts crucial in mathematics, science, and even everyday life. We will explore the methods of solving this problem, discuss the significance of remainders, and illuminate the practical relevance of division in diverse contexts.
Understanding the Fundamentals of Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially represents the process of splitting a quantity into equal parts or groups. In the equation 1112 ÷ 3, we are asking: "How many times does 3 go into 1112?" The result of this division provides the answer to that question. While a calculator readily provides the answer, understanding the why behind the calculation is far more important for developing a strong mathematical foundation.
Methods for Solving 1112 ÷ 3
Several methods exist for solving this division problem. Let's explore a few:
1. Long Division: This traditional method involves a step-by-step process:
- Step 1: Divide the first digit of the dividend (1112) by the divisor (3). 3 doesn't go into 1, so we move to the first two digits: 11.
- Step 2: 3 goes into 11 three times (3 x 3 = 9). Write the '3' above the '1' in the quotient.
- Step 3: Subtract 9 from 11, leaving 2.
- Step 4: Bring down the next digit (1). Now we have 21.
- Step 5: 3 goes into 21 seven times (3 x 7 = 21). Write the '7' above the '1' in the quotient.
- Step 6: Subtract 21 from 21, leaving 0.
- Step 7: Bring down the last digit (2). Now we have 2.
- Step 8: 3 goes into 2 zero times. Write '0' above the '2' in the quotient.
- Step 9: The remainder is 2.
Therefore, 1112 ÷ 3 = 370 with a remainder of 2. This can also be expressed as 370 R2 or 370 2/3.
2. Repeated Subtraction: This method involves repeatedly subtracting the divisor from the dividend until the result is less than the divisor. The number of subtractions performed equals the quotient, and the final remainder is the remaining value. While this method is less efficient for larger numbers, it demonstrates the underlying concept of division clearly.
3. Using a Calculator: The simplest method is to use a calculator. Inputting 1112 ÷ 3 will immediately provide the answer: 370.666... The calculator shows the decimal representation, which is equivalent to 370 with a remainder of 2.
The Significance of Remainders
The remainder (2 in this case) is a crucial part of the result. It indicates that the dividend (1112) cannot be perfectly divided into equal groups of the divisor (3). This remainder has practical implications. For instance, if you have 1112 apples and want to divide them equally among 3 people, each person receives 370 apples, and there are 2 apples left over. The remainder highlights the inexact nature of the division in certain scenarios.
Applications of Division in Real-World Scenarios
Division is not confined to abstract mathematical exercises. It finds extensive application in various fields:
-
Everyday Life: Dividing costs among friends, sharing resources, calculating unit prices, splitting bills, portioning ingredients in cooking, and distributing tasks equally all involve division.
-
Engineering and Physics: Division is fundamental in calculating ratios, proportions, velocities, accelerations, forces, and many other engineering and physics problems. For instance, calculating the average speed involves dividing the total distance by the total time.
-
Computer Science: Division is a core operation in computer algorithms, data structures, and programming. Many sorting and searching algorithms rely on division for efficiency. Memory allocation and data processing frequently employ division operations.
-
Finance and Accounting: Division is vital in calculating percentages, interest rates, profit margins, and many other financial metrics. Budgeting and resource allocation also rely heavily on division.
-
Statistics: Division is used in calculating averages, means, medians, standard deviations, and other statistical measures. Understanding the distribution of data often involves dividing data sets into groups.
-
Business and Economics: Division is used extensively in calculating market shares, ratios of profitability, economic indicators, and other business metrics.
Exploring Further Mathematical Concepts Related to Division
Understanding 1112 ÷ 3 opens doors to further exploration of various mathematical concepts:
-
Fractions: The result with a remainder can be expressed as a fraction (2/3 in this case), demonstrating the link between division and fractions. Understanding fractions is essential for more advanced mathematical concepts.
-
Decimals: The decimal representation (370.666...) provides another way to represent the result, illustrating the relationship between division and decimals. Decimals are widely used in many scientific and technical applications.
-
Modular Arithmetic: The remainder (2) is also significant in modular arithmetic, a branch of number theory where numbers "wrap around" upon reaching a certain value (the modulus). Modular arithmetic is fundamental in cryptography and computer science.
-
Prime Numbers and Factorization: Dividing by 3 helps understand prime factorization. Although 3 is a factor of 1110 (which is 1112 -2), exploring whether other numbers are factors of 1112 is relevant to understanding prime numbers and their properties.
-
Algebra: Division forms a cornerstone of algebraic manipulations. Solving equations often involves dividing both sides of an equation by a constant.
Frequently Asked Questions (FAQs)
Q: What is the exact answer to 1112 divided by 3?
A: The exact answer is 370 with a remainder of 2, or 370 2/3, or approximately 370.666...
Q: Why is there a remainder?
A: A remainder occurs when the dividend (1112) is not perfectly divisible by the divisor (3). It signifies that the division does not result in a whole number.
Q: How can I check my answer?
A: You can check your answer by multiplying the quotient (370) by the divisor (3) and adding the remainder (2). The result should be the original dividend (1112): (370 x 3) + 2 = 1112.
Q: What are some real-world examples of division with remainders?
A: Sharing 1112 candies equally among 3 children leaves 2 candies remaining. Dividing a 1112-meter track into 3 equal sections leaves a 2-meter remaining section.
Conclusion
The seemingly simple calculation of 1112 divided by 3 opens a window into the fascinating world of mathematics. It showcases not only the basic arithmetic operation of division but also its intricate connections to fractions, decimals, modular arithmetic, and other advanced mathematical concepts. Understanding this calculation extends far beyond a simple numerical answer; it demonstrates the fundamental role division plays in various aspects of life, from everyday tasks to complex scientific and technological applications. By grasping the underlying principles, we develop a stronger mathematical intuition and a greater appreciation for the power and elegance of mathematics. This exploration encourages further investigation into the beauty and practicality of mathematical concepts, proving that even the simplest arithmetic operation can be a gateway to deeper understanding.
Latest Posts
Latest Posts
-
8 Quarts How Many Liters
Sep 16, 2025
-
How Many Spoons Is 15ml
Sep 16, 2025
-
Sudden Wind Gusts On Highways
Sep 16, 2025
-
A Sustainable Society Would Emphasize
Sep 16, 2025
-
How Many Cups In 2l
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1 12 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.