1 2 6 24 120
cibeltiagestion
Sep 03, 2025 · 5 min read
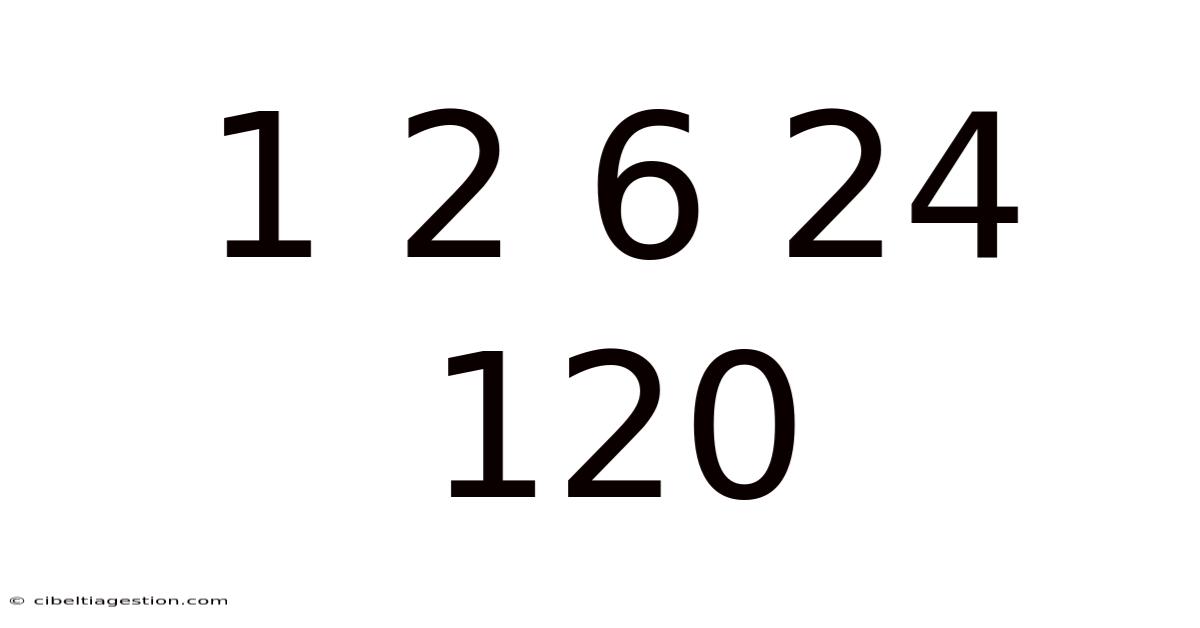
Table of Contents
Decoding the Sequence: Unveiling the Patterns and Power of 1, 2, 6, 24, 120
This article delves into the fascinating mathematical sequence: 1, 2, 6, 24, 120... Understanding this sequence unlocks the door to exploring factorials, combinatorics, and their significant applications in various fields, from probability and statistics to computer science and even physics. We'll unravel the underlying patterns, explore its mathematical definition, and delve into its practical uses. This journey will not only reveal the beauty of mathematics but also empower you with a deeper understanding of its practical applications.
Introduction: Recognizing the Pattern
At first glance, the sequence 1, 2, 6, 24, 120 might seem random. However, a closer examination reveals a clear and elegant pattern: each number is the product of its preceding number and the next consecutive integer.
- 1 x 2 = 2
- 2 x 3 = 6
- 6 x 4 = 24
- 24 x 5 = 120
This pattern immediately suggests a connection to a fundamental mathematical concept: factorials.
Understanding Factorials: The Heart of the Sequence
A factorial, denoted by the symbol "!", is the product of all positive integers less than or equal to a given positive integer. For example:
- 1! = 1
- 2! = 1 x 2 = 2
- 3! = 1 x 2 x 3 = 6
- 4! = 1 x 2 x 3 x 4 = 24
- 5! = 1 x 2 x 3 x 4 x 5 = 120
Therefore, our sequence 1, 2, 6, 24, 120 is simply the sequence of factorials: 1!, 2!, 3!, 4!, 5! This seemingly simple observation opens up a world of mathematical possibilities.
Beyond the Basics: Extending the Sequence and its Implications
The sequence can be extended indefinitely by continuing the pattern:
- 6! = 720
- 7! = 5040
- 8! = 40320
- and so on...
The values of factorials grow rapidly. This rapid growth has significant implications in various fields. For instance, in probability calculations, factorials appear frequently in formulas for permutations and combinations. Understanding factorials is crucial for determining the number of ways to arrange objects or select subsets from a larger set.
Factorials in Combinatorics and Probability
Combinatorics is the branch of mathematics that deals with counting, arranging, and selecting objects. Factorials are fundamental building blocks in many combinatorial formulas. Here are a few key examples:
-
Permutations: A permutation is an arrangement of objects in a specific order. The number of permutations of n distinct objects is n!. For example, there are 3! = 6 ways to arrange three distinct objects.
-
Combinations: A combination is a selection of objects where the order does not matter. The number of combinations of selecting k objects from a set of n objects is given by the binomial coefficient: ⁿCₖ = n! / (k!(n-k)!). This formula relies heavily on factorials.
-
Probability Calculations: In probability, factorials are crucial for calculating probabilities involving permutations and combinations. For example, in card games, the probability of drawing a specific hand depends on the number of possible permutations or combinations of cards.
Applications in Other Fields
The applications of factorials and their associated sequences extend beyond basic combinatorics and probability. Here are a few examples:
-
Computer Science: Factorials play a role in algorithm analysis, especially in areas like sorting and searching. The complexity of some algorithms is directly related to factorial functions.
-
Physics: Factorials appear in various physics equations, particularly in quantum mechanics and statistical mechanics. For instance, they're used in calculations involving particle distributions and probability distributions.
-
Taylor Series Expansion: Factorials are essential components in the Taylor series expansion, a powerful tool used to approximate functions using infinite sums. This technique is widely used in various scientific and engineering applications.
-
Calculus and Analysis: The factorial function is closely related to the Gamma function, a generalization of the factorial function to complex numbers. The Gamma function is a fundamental tool in advanced calculus and analysis.
The Gamma Function: A Generalization of Factorials
The Gamma function, denoted as Γ(z), is a generalization of the factorial function to complex numbers. For positive integers, Γ(n) = (n-1)!. This means the Gamma function extends the concept of factorials beyond positive integers to encompass complex numbers. This extension is incredibly useful in advanced mathematical analysis and has significant applications in various scientific fields.
Limitations and Approximations of Factorials
While factorials are powerful mathematical tools, calculating large factorials can be computationally expensive. The values grow extremely quickly, leading to potential overflow errors in computer programs. As a result, approximation methods are often used for large factorials. Stirling's approximation is a commonly used method for approximating large factorials:
n! ≈ √(2πn) * (n/e)^n
This approximation provides a reasonably accurate estimate of large factorials, avoiding the computational challenges associated with direct calculation.
Frequently Asked Questions (FAQ)
Q: What is the next number in the sequence 1, 2, 6, 24, 120?
A: The next number is 720 (6!).
Q: How do I calculate a large factorial like 100!?
A: Calculating 100! directly is computationally expensive. You would typically use a computer program or a calculator with high precision capabilities, or utilize Stirling's approximation for an approximate value.
Q: What are some real-world applications of factorials?
A: Factorials are used extensively in probability and statistics, computer science, physics, and various engineering disciplines. They are crucial in calculating permutations, combinations, and in many formulas used to model real-world phenomena.
Q: What is the significance of the Gamma function?
A: The Gamma function is a powerful generalization of the factorial function, extending it to complex numbers. This extension opens up a vast range of applications in advanced mathematical analysis and various scientific fields.
Conclusion: The Enduring Power of Simple Sequences
The seemingly simple sequence 1, 2, 6, 24, 120, representing the factorials, reveals a profound mathematical concept with far-reaching implications. From basic combinatorics and probability to advanced calculus and physics, the power of factorials underscores the interconnectedness of mathematical ideas and their capacity to model complex phenomena. Understanding this sequence provides a gateway to a deeper appreciation of the elegance and utility of mathematics in diverse fields. The journey from recognizing a simple pattern to understanding its underlying principles and applications highlights the rewarding nature of mathematical exploration and its profound impact on our world. This exploration is a testament to the enduring power of seemingly simple mathematical sequences and their ability to unlock a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
What Is Half Of 55
Sep 05, 2025
-
Knowing About Knowing Is Called
Sep 05, 2025
-
The Most Dangerous Game Summary
Sep 05, 2025
-
64 Kg How Many Lbs
Sep 05, 2025
-
All The Factors For 18
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about 1 2 6 24 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.