1 2 Divided By 6
cibeltiagestion
Sep 12, 2025 · 5 min read
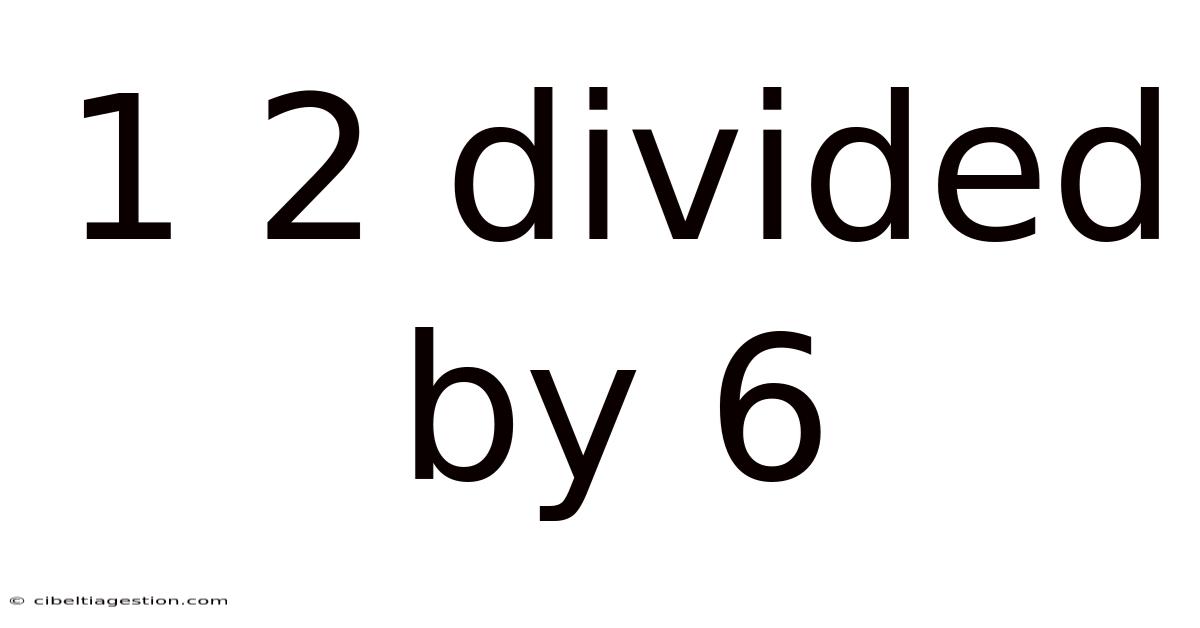
Table of Contents
Unpacking the Mystery: 1/2 Divided by 6
This article delves into the seemingly simple, yet surprisingly nuanced, mathematical problem of 1/2 divided by 6. While the calculation itself might seem trivial at first glance, understanding the underlying principles reveals fundamental concepts in fractions, division, and mathematical reasoning. This exploration goes beyond a simple numerical answer; we'll unpack the "why" behind the solution, offering various approaches to solidify your understanding. This guide is perfect for anyone looking to refresh their fraction skills or gain a deeper understanding of division involving fractions.
Understanding Fractions: A Quick Refresher
Before diving into the division problem, let's briefly review the core concepts of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For example, in the fraction 1/2 (one-half), the numerator (1) signifies we have one part, and the denominator (2) signifies the whole is divided into two equal parts.
Different Approaches to Solving 1/2 ÷ 6
Now, let's tackle the problem of 1/2 ÷ 6. There are several ways to approach this, each offering a slightly different perspective on the underlying mathematical principles:
1. The Reciprocal Method:
This method utilizes the concept of reciprocals. The reciprocal of a fraction is obtained by swapping its numerator and denominator. For instance, the reciprocal of 2/3 is 3/2. Dividing by a number is the same as multiplying by its reciprocal.
Therefore, 1/2 ÷ 6 can be rewritten as:
1/2 × (1/6)
Multiplying the numerators and the denominators, we get:
(1 × 1) / (2 × 6) = 1/12
Therefore, 1/2 divided by 6 equals 1/12.
2. Visual Representation: Using a Fraction Model
Imagine a pizza cut into two equal halves. You have one of those halves (1/2). Now, you need to divide this half-pizza into six equal parts. To do this, you would further divide each of the two original halves into six smaller slices. This results in a total of twelve slices (2 x 6 = 12). Since you started with only one of the original halves, you now have one out of twelve slices (1/12). This visual representation directly shows the result of 1/2 ÷ 6 = 1/12.
3. Converting to Decimal Numbers
Another approach involves converting the fraction 1/2 to its decimal equivalent (0.5). Then, you can perform the division:
0.5 ÷ 6 = 0.08333...
This decimal representation, while accurate, may not always be practical. The fractional representation (1/12) often provides a more precise and easily understandable result, especially in contexts where dealing with precise portions is important.
The Importance of Understanding the Process
It's crucial to understand that the solution, 1/12, isn't just a random number. It represents a specific portion or fraction of the original whole. The process of dividing a fraction by a whole number inherently reduces the size of the original fraction. In this case, dividing 1/2 by 6 results in a significantly smaller fraction, 1/12, highlighting the impact of dividing a part (1/2) into an even larger number of parts (6).
Expanding the Concept: Dividing Fractions by Fractions
Let's extend our understanding beyond dividing a fraction by a whole number. Consider the more general case of dividing one fraction by another fraction: a/b ÷ c/d.
The process remains similar. We convert the division into multiplication by using the reciprocal of the second fraction:
a/b ÷ c/d = a/b × d/c = (a × d) / (b × c)
This formula provides a versatile tool for tackling various fraction division problems.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve 1/2 ÷ 6?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is more important than simply obtaining an answer using a calculator. Knowing how to solve the problem allows you to apply the concepts to more complex problems.
Q: What if the denominator of the fraction is zero?
A: Division by zero is undefined in mathematics. It's a crucial concept to grasp. There is no number that, when multiplied by zero, gives you a non-zero result. Therefore, a fraction with a denominator of zero is not a valid mathematical expression.
Q: Are there other real-world applications of this type of calculation?
A: Yes! Dividing fractions is frequently used in various fields, including:
- Baking: Dividing recipes to adjust serving sizes.
- Construction: Calculating material quantities.
- Engineering: Determining proportions and scaling.
- Finance: Calculating portions of investments or shares.
Advanced Concepts: Mixed Numbers and Improper Fractions
To further enhance your understanding, let's briefly introduce mixed numbers and improper fractions.
A mixed number combines a whole number and a fraction (e.g., 1 1/2). An improper fraction has a numerator larger than or equal to its denominator (e.g., 3/2). When performing division with mixed numbers, it is often easier to convert them into improper fractions before applying the division rules. For example, 1 1/2 can be converted to 3/2.
Conclusion: Mastering Fractions – A Building Block of Mathematics
Understanding the division of fractions, exemplified by the problem 1/2 ÷ 6, is a fundamental skill in mathematics. The ability to confidently perform these calculations extends beyond simply obtaining the correct numerical answer. It's about developing a solid grasp of mathematical principles, fostering logical reasoning, and building a strong foundation for more advanced mathematical concepts. Whether you are a student, a professional, or simply someone curious about mathematics, mastering fractions is a rewarding investment in your intellectual capabilities. By understanding the different approaches—the reciprocal method, visual representation, and conversion to decimals—you gain a deeper appreciation for the underlying logic and versatility of fractional arithmetic. Remember, the journey of learning mathematics is a continuous process of exploration and discovery. Each problem solved, each concept grasped, brings you closer to a more comprehensive understanding of the world around us. So, keep practicing, keep questioning, and keep exploring the fascinating world of numbers!
Latest Posts
Latest Posts
-
What Is 65 Of 65
Sep 12, 2025
-
Barcode Label Unreadable And Replaced
Sep 12, 2025
-
110 Sq Meters To Feet
Sep 12, 2025
-
Ellos 1 Of 1 Espanol
Sep 12, 2025
-
Abbreviated Electron Configuration Of Radium
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Divided By 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.