1 3/4 Divided By 2
cibeltiagestion
Sep 09, 2025 · 5 min read
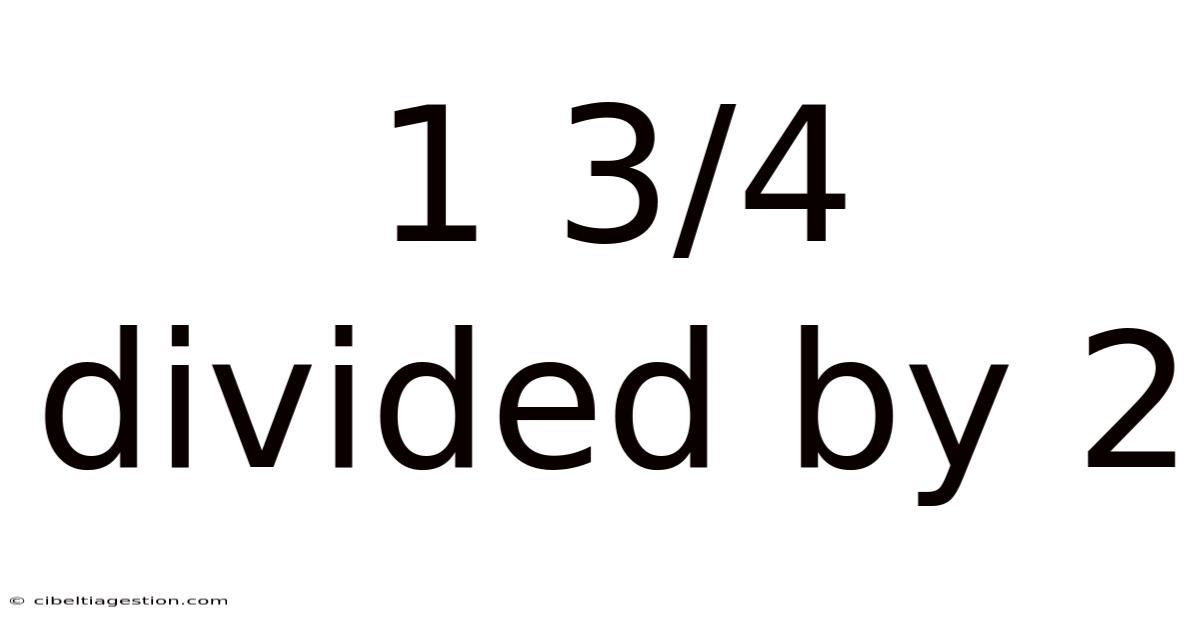
Table of Contents
Decoding 1 3/4 Divided by 2: A Comprehensive Guide
Dividing fractions and mixed numbers can seem daunting, but with a clear understanding of the process, it becomes straightforward. This article will comprehensively guide you through solving 1 3/4 divided by 2, explaining the steps involved, the underlying mathematical principles, and offering practical applications. We'll explore various methods and delve into the reasoning behind each step, ensuring a solid grasp of the concept. This guide is perfect for students struggling with fraction division, as well as anyone looking to refresh their understanding of basic arithmetic.
Understanding the Problem: 1 3/4 ÷ 2
Our problem, 1 3/4 ÷ 2, asks us to determine how many times the number 2 fits into 1 3/4. This can be visualized as sharing 1 3/4 pizzas equally amongst 2 people. Intuitively, we know the answer will be less than 1, as 2 is larger than 1 3/4. Let's break down the solution using several different approaches.
Method 1: Converting to Improper Fractions
This is a widely used and efficient method. It involves converting the mixed number (1 3/4) into an improper fraction before performing the division.
Step 1: Convert the mixed number to an improper fraction.
To do this, multiply the whole number (1) by the denominator (4), add the numerator (3), and keep the same denominator. This gives us:
1 3/4 = (1 * 4 + 3) / 4 = 7/4
Step 2: Rewrite the division problem.
Our problem now becomes: 7/4 ÷ 2
Step 3: Convert the whole number to a fraction.
Any whole number can be expressed as a fraction with a denominator of 1. Therefore, 2 becomes 2/1. Our problem is now:
7/4 ÷ 2/1
Step 4: Invert the second fraction and multiply.
Dividing by a fraction is the same as multiplying by its reciprocal (inverse). We invert the second fraction (2/1 becomes 1/2) and change the division sign to a multiplication sign:
7/4 x 1/2
Step 5: Multiply the numerators and the denominators.
Multiply the numerators together (7 x 1 = 7) and the denominators together (4 x 2 = 8). This results in:
7/8
Therefore, 1 3/4 divided by 2 equals 7/8.
Method 2: Using Decimal Representation
Another approach is to convert both the mixed number and the whole number into decimal form before performing the division.
Step 1: Convert the mixed number to a decimal.
1 3/4 can be converted to a decimal by dividing the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75. Therefore, 1 3/4 = 1.75
Step 2: Perform the division.
Now divide 1.75 by 2: 1.75 ÷ 2 = 0.875
Therefore, 1 3/4 divided by 2 equals 0.875. Note that this decimal is equivalent to the fraction 7/8 (you can verify this by performing the division 7 ÷ 8).
Method 3: Breaking Down the Problem
This approach involves visualizing the division process more intuitively.
We are dividing 1 3/4 by 2. This means we are splitting 1 3/4 into two equal parts.
- First, divide the whole number: Dividing 1 by 2 gives us 1/2 or 0.5.
- Then, divide the fraction: Dividing 3/4 by 2 can be written as (3/4) ÷ 2, which simplifies to 3/8 (multiplying by the reciprocal 1/2).
- Add the results: Adding the two parts together: 1/2 + 3/8 = 4/8 + 3/8 = 7/8.
Again, this confirms that 1 3/4 divided by 2 equals 7/8.
The Mathematical Principle: Reciprocals and Division
The core mathematical principle behind dividing fractions is the concept of reciprocals. The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 2 is 1/2, and the reciprocal of 3/4 is 4/3.
When dividing by a fraction, we multiply by its reciprocal. This is because division is the inverse operation of multiplication. Imagine you have the equation a ÷ b = c. Multiplying both sides by b gives you a = b * c. This demonstrates the relationship between division and multiplication. Therefore, when we change from division to multiplication using reciprocals, we are essentially applying this fundamental inverse relationship.
Real-World Applications
Understanding fraction division is crucial in numerous real-world scenarios:
- Cooking: Scaling down recipes often involves dividing fractional quantities.
- Sewing: Calculating fabric requirements necessitates dividing lengths and widths.
- Construction: Precise measurements in construction projects heavily rely on fraction manipulation.
- Finance: Dividing shares or calculating percentages frequently involve fractions.
- Data analysis: Interpreting data sets often involves working with fractions and ratios.
Frequently Asked Questions (FAQ)
Q: Why do we invert and multiply when dividing fractions?
A: This stems from the inverse relationship between multiplication and division. Inverting and multiplying is a shortcut that simplifies the process and makes it easier to solve.
Q: Can I use a calculator to solve this problem?
A: Yes, most calculators can handle fraction division. You can either input the numbers directly as fractions (if your calculator supports it) or convert the mixed number and whole number to decimals before dividing.
Q: Is there only one correct way to solve this problem?
A: While there are different methods, as demonstrated, they all lead to the same correct answer: 7/8 or 0.875. The best method depends on individual preference and the specific context of the problem.
Q: What if I have to divide a mixed number by another mixed number?
A: Follow the same principle: convert both mixed numbers to improper fractions, invert the second fraction, and multiply.
Conclusion
Dividing 1 3/4 by 2, whether approached using improper fractions, decimal conversion, or a more intuitive breakdown, consistently yields the same result: 7/8. This problem highlights the importance of understanding fundamental mathematical concepts, such as converting mixed numbers, finding reciprocals, and applying the inverse relationship between multiplication and division. Mastering these concepts empowers you to tackle a wide range of mathematical challenges in various real-world applications, enhancing your problem-solving skills and numerical fluency. Remember, practice is key to solidifying your understanding and building confidence in handling fraction division. Don't hesitate to work through similar problems to further reinforce your learning.
Latest Posts
Latest Posts
-
Jawaharlal Nehru Would Be Considered
Sep 09, 2025
-
Tracing Substances Through The Kidney
Sep 09, 2025
-
The Sentence Length Is Generally
Sep 09, 2025
-
Companies Should View Whistleblowers As
Sep 09, 2025
-
The Value Of 10 Is
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 1 3/4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.