1 3 X 10 4
cibeltiagestion
Sep 05, 2025 · 7 min read
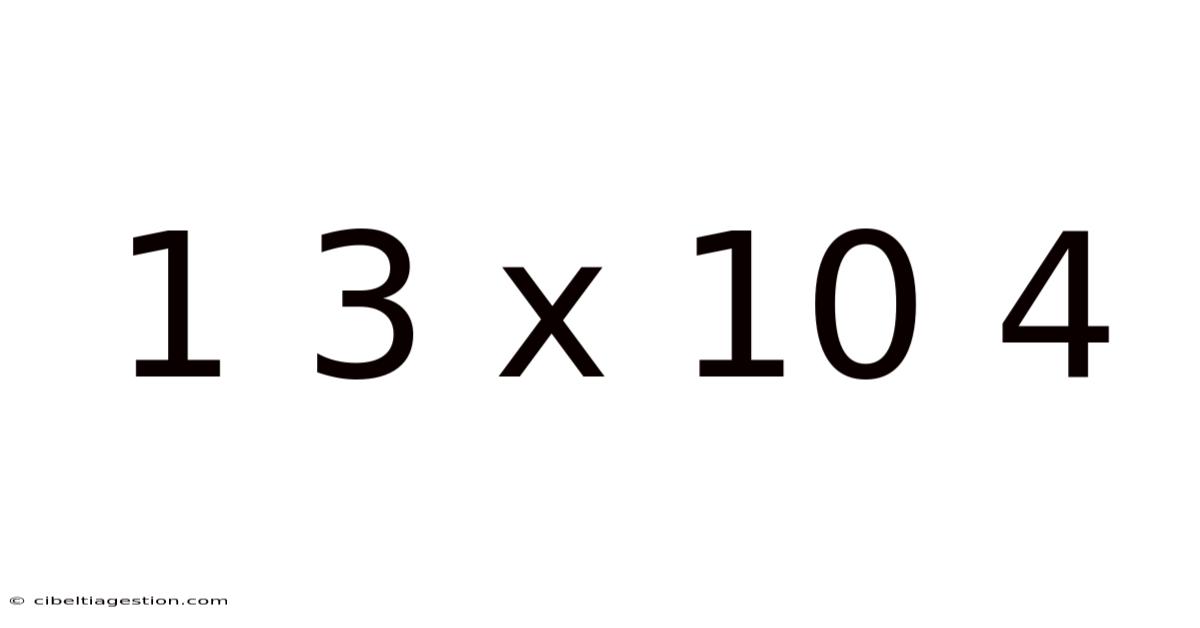
Table of Contents
Decoding 1.3 x 10⁴: Scientific Notation and its Applications
Scientific notation, a cornerstone of scientific communication, provides a concise and efficient way to represent extremely large or extremely small numbers. Understanding scientific notation is crucial in various fields, from physics and chemistry to astronomy and computer science. This article delves deep into the meaning and applications of the number 1.3 x 10⁴, explaining its calculation, significance, and real-world examples. We’ll explore how this seemingly simple expression can represent vast quantities and how its understanding unlocks a deeper appreciation of the scale of the universe and the precision of scientific measurement.
Understanding Scientific Notation
Scientific notation expresses numbers in the form a x 10<sup>b</sup>, where 'a' is a number between 1 and 10 (but not including 10), and 'b' is an integer representing the power of 10. This system simplifies the representation of very large or very small numbers, avoiding long strings of zeros. For instance, the distance from the Earth to the Sun, approximately 150,000,000,000 meters, is much more easily represented in scientific notation as 1.5 x 10<sup>11</sup> meters.
Breaking Down 1.3 x 10⁴
Let's focus on the number in question: 1.3 x 10⁴. This notation signifies a number where 'a' is 1.3 and 'b' is 4. To convert this from scientific notation to standard notation, we simply multiply 1.3 by 10 raised to the power of 4. This means we move the decimal point in 1.3 four places to the right.
Therefore, 1.3 x 10⁴ = 13,000.
Real-World Applications of Numbers Expressed in Scientific Notation
Scientific notation's power lies in its ability to manage scales that are beyond our everyday comprehension. Here are several examples where numbers similar to 1.3 x 10⁴, or expressed in scientific notation, are crucial:
-
Population Statistics: The population of a medium-sized city might be represented by a number similar to 1.3 x 10⁴. While not exactly 13,000, the scientific notation allows for a quick comparison with other city populations also expressed in this manner. This allows for easier data analysis and comparison between different datasets. Scientists use this method for efficient population modeling and forecasting.
-
Financial Markets: The daily trading volume of a specific stock or the total assets under management of a particular investment firm could be expressed in scientific notation, especially when dealing with incredibly large sums of money. This simplified representation is critical for clear and efficient communication in the financial world.
-
Environmental Science: Measurements related to pollution levels, such as the number of particulate matter (PM2.5) particles per cubic meter of air in a heavily polluted area, might be represented using scientific notation. This precise representation helps in environmental modeling and risk assessment. The scale and impact of environmental changes are more easily understood through this notation.
-
Astronomy and Cosmology: In astronomy, the sheer scale of distances involved necessitates the use of scientific notation. The distance to nearby stars, the size of planets, or the number of atoms in a star are all incredibly large numbers best represented in this concise format. For instance, the mass of the Sun is approximately 1.989 x 10<sup>30</sup> kg. The use of scientific notation helps to simplify calculations and improve the readability of astronomical data.
-
Microscopy and Nanotechnology: At the other end of the scale, scientific notation is essential in representing the incredibly small dimensions encountered in microscopy and nanotechnology. The size of a virus, the wavelength of light, or the diameter of a carbon nanotube are all exceedingly small and are most easily expressed using scientific notation. This precise measurement is critical for development in nanotechnology.
-
Computer Science and Data Storage: In computer science, the number of bytes in a large data file or the processing power of a supercomputer is often expressed in scientific notation. This helps in comparing the capacity and performance of different systems. For example, the storage capacity of a large hard drive might be represented as 1.5 x 10<sup>12</sup> bytes (1.5 terabytes).
Working with Scientific Notation: Multiplication and Division
Manipulating numbers in scientific notation requires understanding the rules of exponents. Here's how multiplication and division work:
-
Multiplication: To multiply two numbers in scientific notation, multiply the 'a' values and add the 'b' values. For example: (2.5 x 10³) x (3 x 10²) = (2.5 x 3) x 10<sup>(3+2)</sup> = 7.5 x 10⁵
-
Division: To divide two numbers in scientific notation, divide the 'a' values and subtract the 'b' values. For example: (7.5 x 10⁵) / (2.5 x 10³) = (7.5 / 2.5) x 10<sup>(5-3)</sup> = 3 x 10²
Converting to and from Scientific Notation
The ability to convert numbers between standard and scientific notation is fundamental.
-
From Standard to Scientific: To convert a number from standard notation to scientific notation, move the decimal point to the left until you have a number between 1 and 10. The number of places you moved the decimal point becomes the exponent of 10. If you moved the decimal point to the left, the exponent is positive; if you moved it to the right, the exponent is negative.
-
From Scientific to Standard: To convert a number from scientific notation to standard notation, move the decimal point in the 'a' value the number of places indicated by the exponent of 10. If the exponent is positive, move the decimal point to the right; if the exponent is negative, move it to the left.
Further Applications and Significance
The number 1.3 x 10⁴, while seemingly simple, highlights the power and practicality of scientific notation. Its applications extend far beyond the examples given, encompassing diverse scientific and engineering disciplines. The ability to accurately represent and manipulate extremely large and small numbers is critical for accurate modeling, prediction, and problem-solving in many fields. The widespread use of scientific notation underscores its importance in fostering clear communication and efficient data handling within the scientific community. Moreover, it lays the foundation for understanding the vast scales encountered in the natural world, from the subatomic realm to the cosmos.
Frequently Asked Questions (FAQ)
Q: What is the difference between 1.3 x 10⁴ and 1.3 x 10⁻⁴?
A: The difference lies in the exponent. 1.3 x 10⁴ represents a relatively large number (13,000), while 1.3 x 10⁻⁴ represents a very small number (0.00013). The positive exponent indicates a large number, while the negative exponent indicates a small number.
Q: Why is scientific notation important?
A: Scientific notation is crucial because it provides a concise and efficient way to represent very large and very small numbers, making them easier to work with, understand, and communicate. It avoids the cumbersome use of many zeros, improving clarity and reducing the chance of errors.
Q: Can any number be expressed in scientific notation?
A: Yes, any number can be expressed in scientific notation. Even simple numbers like 5 can be written as 5 x 10⁰.
Q: How do I perform addition and subtraction with numbers in scientific notation?
A: Addition and subtraction with numbers in scientific notation require converting the numbers to standard notation first, performing the operation, and then converting the result back to scientific notation if necessary. This ensures accuracy and prevents potential errors associated with directly manipulating exponents.
Q: Are there any limitations to scientific notation?
A: While highly effective, scientific notation is primarily used for representing numerical values. It does not inherently convey qualitative information or context about the data it represents. Proper interpretation always requires understanding the context of the numbers being used.
Conclusion
The seemingly simple expression 1.3 x 10⁴ represents much more than just a number. It's a powerful tool that simplifies the representation and manipulation of vast quantities, critical across many scientific and technical fields. By understanding scientific notation and its applications, we gain a deeper appreciation of the scales involved in the natural world and the precision required in scientific measurement. This concise and efficient system is an essential element of scientific literacy and provides a framework for comprehending the universe's vastness and the intricacies of the microscopic world. Its mastery unlocks a greater understanding of the quantitative nature of reality.
Latest Posts
Latest Posts
-
Is 42 A Prime Number
Sep 05, 2025
-
What Is The Portable Pelican
Sep 05, 2025
-
Polymers That Contain Sugars
Sep 05, 2025
-
Electron Dot Structure For Lithium
Sep 05, 2025
-
Without Adjusting The Column Widths
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about 1 3 X 10 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.