1 4 As A Percentage
cibeltiagestion
Sep 13, 2025 · 5 min read
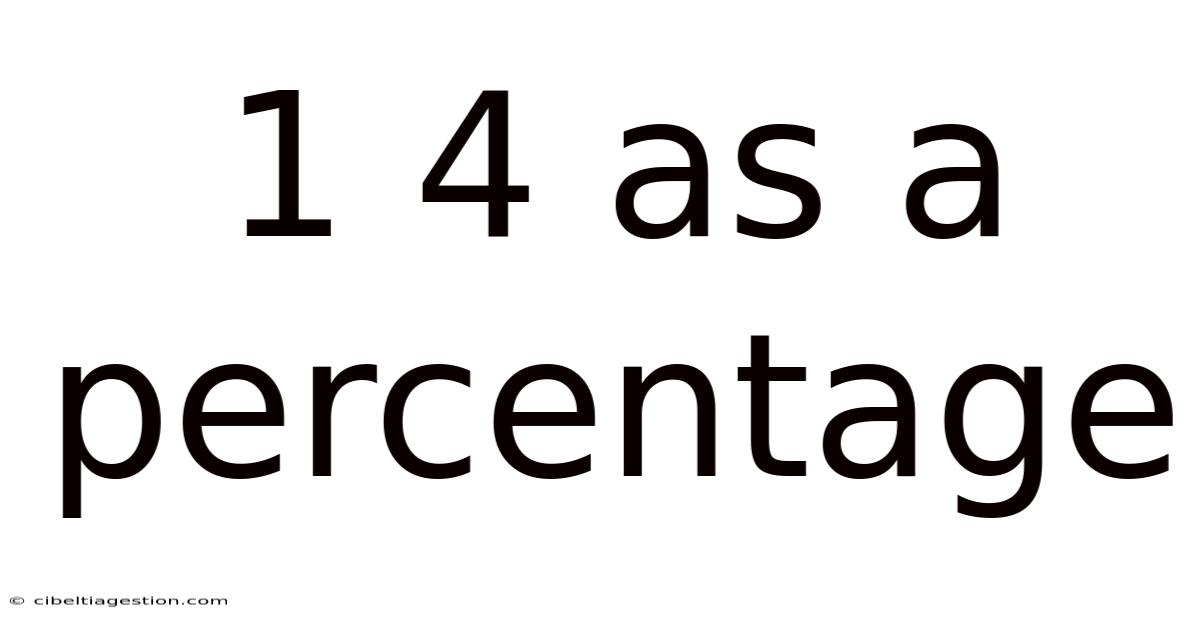
Table of Contents
Understanding 1/4 as a Percentage: A Comprehensive Guide
What is 1/4 as a percentage? This seemingly simple question opens the door to a deeper understanding of fractions, decimals, and percentages – fundamental concepts in mathematics crucial for everyday life and various academic pursuits. This comprehensive guide will not only answer this question but also explore the underlying principles, provide practical examples, and delve into related concepts to solidify your grasp of this essential mathematical skill.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before we dive into calculating 1/4 as a percentage, let's briefly revisit the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole. A fraction expresses a part as a ratio of two numbers (numerator/denominator). A decimal expresses a part as a number with a decimal point, representing tenths, hundredths, thousandths, and so on. A percentage expresses a part as a fraction of 100, denoted by the symbol %. They are all interchangeable, offering different perspectives on the same numerical value. Understanding their interconnectedness is key to mastering mathematical calculations.
Calculating 1/4 as a Percentage: The Step-by-Step Approach
There are several ways to convert the fraction 1/4 into a percentage. Let's explore the most common methods:
Method 1: Using the Division Method
This is perhaps the most straightforward approach. To convert a fraction to a percentage, you simply divide the numerator by the denominator and then multiply the result by 100.
- Divide the numerator by the denominator: 1 ÷ 4 = 0.25
- Multiply the result by 100: 0.25 × 100 = 25
- Add the percentage symbol: 25%
Therefore, 1/4 is equal to 25%.
Method 2: Understanding Equivalent Fractions
Percentages are essentially fractions with a denominator of 100. We can convert 1/4 into an equivalent fraction with a denominator of 100.
- Find the multiplier: To change the denominator from 4 to 100, we multiply by 25 (100 ÷ 4 = 25).
- Multiply both the numerator and the denominator by the multiplier: (1 × 25) / (4 × 25) = 25/100
- Express as a percentage: 25/100 represents 25 out of 100, which is 25%.
This method highlights the fundamental concept of equivalent fractions – fractions that have the same value despite having different numerators and denominators.
Practical Applications of 1/4 (25%) in Real-Life Scenarios
Understanding 1/4 as 25% has numerous practical applications in various daily situations:
- Shopping Discounts: A 25% discount on a $100 item means a saving of $25 (25% of $100).
- Calculating Tips: Leaving a 25% tip on a $40 meal involves calculating 25% of $40, which is $10.
- Portioning Ingredients: Dividing a recipe that serves 4 into individual servings requires dividing each ingredient quantity by 4 (or taking 25% of the total quantity).
- Financial Calculations: Understanding interest rates, tax rates, and profit margins often involves working with percentages, including 25%. For instance, a 25% increase in salary means your salary will be multiplied by 1.25.
- Data Analysis: Representing data visually using pie charts or bar graphs often uses percentages. A segment representing 1/4 of the data will be shown as 25%.
Beyond 1/4: Exploring Other Fractions and their Percentage Equivalents
Understanding how to convert 1/4 to a percentage helps us understand the broader concept of converting any fraction to a percentage. Let's look at some other common fractions and their percentage equivalents:
- 1/2 = 50%: This represents half of a whole.
- 3/4 = 75%: This represents three-quarters of a whole.
- 1/5 = 20%: This represents one-fifth of a whole.
- 1/10 = 10%: This represents one-tenth of a whole.
- 1/8 = 12.5%: This represents one-eighth of a whole.
By mastering the conversion of these fractions, you build a solid foundation for working with percentages in diverse contexts.
The Scientific Perspective: Understanding Ratios and Proportions
The conversion of fractions to percentages is rooted in the mathematical concepts of ratios and proportions. A ratio compares two quantities, while a proportion states that two ratios are equal. When we convert 1/4 to 25%, we are essentially expressing the ratio 1:4 as an equivalent ratio of 25:100. This underlying principle is fundamental in various scientific and engineering applications, including scaling, modeling, and data analysis.
Frequently Asked Questions (FAQ)
Q1: Can I convert a percentage back into a fraction?
Yes, absolutely! To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, to convert 25% back to a fraction, we do 25/100, which simplifies to 1/4.
Q2: What if the fraction doesn't easily convert to a whole number percentage?
Some fractions result in decimal percentages (e.g., 1/3 ≈ 33.33%). In such cases, you can either round the decimal to a suitable number of decimal places or express the percentage as a mixed number (e.g., 33 1/3%).
Q3: Are there any shortcuts for converting fractions to percentages?
For certain common fractions, you might memorize their percentage equivalents (like 1/2 = 50%, 1/4 = 25%, etc.). However, the division method or the equivalent fractions method remains the most reliable approach for all fractions.
Q4: Why are percentages so important?
Percentages provide a standardized way to compare parts of a whole. They are easily understood and readily applicable in various fields, including finance, statistics, science, and everyday life.
Conclusion: Mastering Percentages – A Gateway to Mathematical Proficiency
Understanding 1/4 as a percentage is more than just a simple conversion; it's a stepping stone to grasping the broader concepts of fractions, decimals, and percentages. By mastering these fundamental mathematical concepts, you equip yourself with valuable skills applicable across numerous academic and real-world scenarios. This understanding forms a crucial foundation for more advanced mathematical concepts and problem-solving in various fields. From managing personal finances to interpreting scientific data, the ability to confidently work with percentages is a key skill for success in the modern world. Remember to practice regularly and explore various methods to build your confidence and proficiency in working with fractions and percentages. The more you practice, the more intuitive these conversions will become.
Latest Posts
Latest Posts
-
How Many Days In March
Sep 13, 2025
-
14 Degrees F To C
Sep 13, 2025
-
Demand Rate For Transcutaneous Pacer
Sep 13, 2025
-
Who Won The 1824 Election
Sep 13, 2025
-
What Aisle Is Cornstarch In
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 1 4 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.