10.25 Divided By Negative 0.5
cibeltiagestion
Sep 09, 2025 · 5 min read
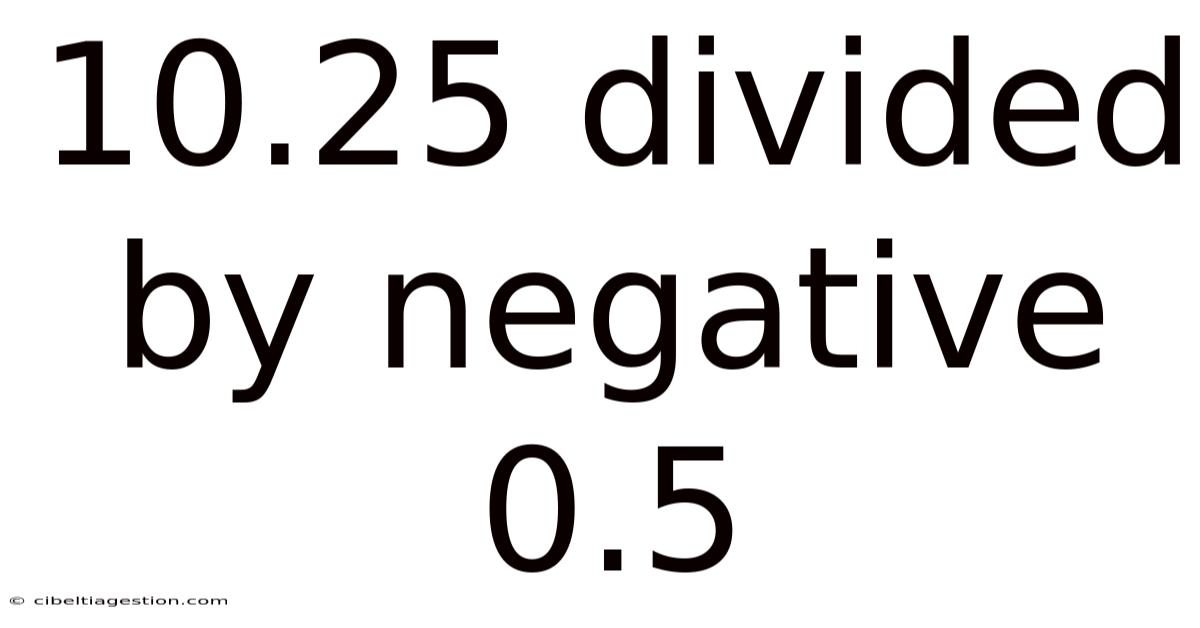
Table of Contents
Diving Deep into Division: Solving 10.25 ÷ -0.5
This article will comprehensively explore the solution to the mathematical problem 10.25 divided by -0.5, providing a step-by-step guide suitable for learners of all levels. We'll delve into the underlying principles of division with decimals and negative numbers, ensuring a thorough understanding beyond just the final answer. This will include practical examples and explanations to solidify your grasp of the concept. Understanding this seemingly simple calculation forms a crucial foundation for more advanced mathematical concepts.
Understanding the Problem: 10.25 ÷ -0.5
Before we jump into the solution, let's break down the problem: 10.25 ÷ -0.5. This involves two key elements:
- Division: This is a fundamental arithmetic operation that determines how many times one number (the divisor) is contained within another number (the dividend). In our case, we are finding out how many times -0.5 goes into 10.25.
- Decimals: Both the dividend (10.25) and the divisor (-0.5) are decimal numbers. This means we need to understand how to handle calculations with numbers that include digits after the decimal point.
- Negative Numbers: The divisor (-0.5) is a negative number. The inclusion of a negative number significantly impacts the sign of the final answer. Remember the rules of signs in division: a positive number divided by a negative number results in a negative number.
Step-by-Step Solution: A Practical Approach
To solve 10.25 ÷ -0.5, we can employ several methods. Let's explore a few, starting with a method that avoids complex decimal manipulations.
Method 1: Converting to Fractions
Converting decimals to fractions often simplifies calculations. Let's rewrite the problem using fractions:
-
Convert decimals to fractions:
- 10.25 can be written as 1025/100 (or simplified to 41/4)
- -0.5 can be written as -5/10 (or simplified to -1/2)
-
Rewrite the division as a multiplication: Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of -1/2 is -2/1 (or simply -2). So our problem becomes:
(41/4) * (-2/1)
-
Perform the multiplication:
(41/4) * (-2/1) = -82/4
-
Simplify the fraction:
-82/4 = -20.5
Therefore, 10.25 ÷ -0.5 = -20.5
Method 2: Long Division with Decimals
While the fraction method is often cleaner, long division offers a more visual approach, particularly helpful for understanding the process.
-
Set up the long division:
_________ -0.5 | 10.25 -
Adjust the divisor: It's generally easier to work with whole numbers as divisors. To achieve this, multiply both the divisor and the dividend by 10:
_________ -5 | 102.5 -
Perform long division:
20.5 -5 | 102.5 -10 02 -0 25 -25 0 -
Consider the sign: Remember, a positive number divided by a negative number results in a negative number. Therefore, the final answer is -20.5.
Mathematical Explanation: Delving Deeper
The solution hinges on several fundamental mathematical concepts:
- The concept of division: Division is essentially repeated subtraction. It answers the question: "How many times can the divisor be subtracted from the dividend before the result becomes zero or less than the divisor?"
- Working with decimals: Decimals represent fractions with denominators that are powers of 10. Calculations with decimals require careful attention to the placement of the decimal point.
- Rules of signs: The rules of signs dictate the outcome of operations involving positive and negative numbers. In division, if the signs of the dividend and divisor are different, the result is negative. If the signs are the same, the result is positive.
- Reciprocal: The reciprocal of a number is simply 1 divided by that number. Multiplying by the reciprocal is an alternative to division, particularly useful when dealing with fractions.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to solve this?
A1: Absolutely! Calculators are excellent tools for performing calculations quickly and accurately. Simply input 10.25 ÷ -0.5 and the calculator will provide the answer -20.5. However, understanding the underlying mathematical principles is crucial for developing problem-solving skills and avoiding reliance on technology for basic calculations.
Q2: What if the divisor was a larger negative number?
A2: The process remains the same. The only difference would be the magnitude of the quotient (the result of the division). For example, if the divisor was -10, the quotient would be -1.025. The principle of dividing a positive by a negative remains.
Q3: Are there other methods to solve this problem?
A3: Yes. One could use the concept of repeated subtraction. Subtracting -0.5 repeatedly from 10.25 until you reach zero (or a value less than -0.5) would lead to the same answer, but this method would be less efficient than the methods described above.
Q4: Why is it important to understand the steps involved rather than just using a calculator?
A4: Understanding the steps ensures a deeper comprehension of the underlying mathematical principles. This understanding is fundamental for tackling more complex problems in algebra, calculus, and other advanced mathematical fields. Using a calculator without understanding the concepts can hinder your ability to solve similar problems in different contexts. It also fosters critical thinking and problem-solving skills, making you a more well-rounded mathematician.
Conclusion: Mastering Decimal Division
Solving 10.25 ÷ -0.5, resulting in -20.5, demonstrates a fundamental application of decimal division and the rules of signs with negative numbers. By employing methods like converting to fractions or using long division, we can clearly visualize and understand the process. Beyond the numerical answer, this problem highlights the importance of understanding the underlying mathematical principles—division, decimals, negative numbers, and reciprocals—to build a strong foundation for more advanced mathematical concepts. The ability to confidently tackle such problems is a cornerstone of mathematical proficiency. Remember to always check your work and consider different methods to reinforce your understanding. Practice makes perfect!
Latest Posts
Latest Posts
-
Reversible Lanes Are Used During
Sep 09, 2025
-
17 12 As A Mixed Number
Sep 09, 2025
-
What Best Describes Hydrostatic Pressure
Sep 09, 2025
-
48 Pounds How Many Kg
Sep 09, 2025
-
How Are Igneous Rocks Formed
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 10.25 Divided By Negative 0.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.