11/10 As A Mixed Number
cibeltiagestion
Sep 14, 2025 · 6 min read
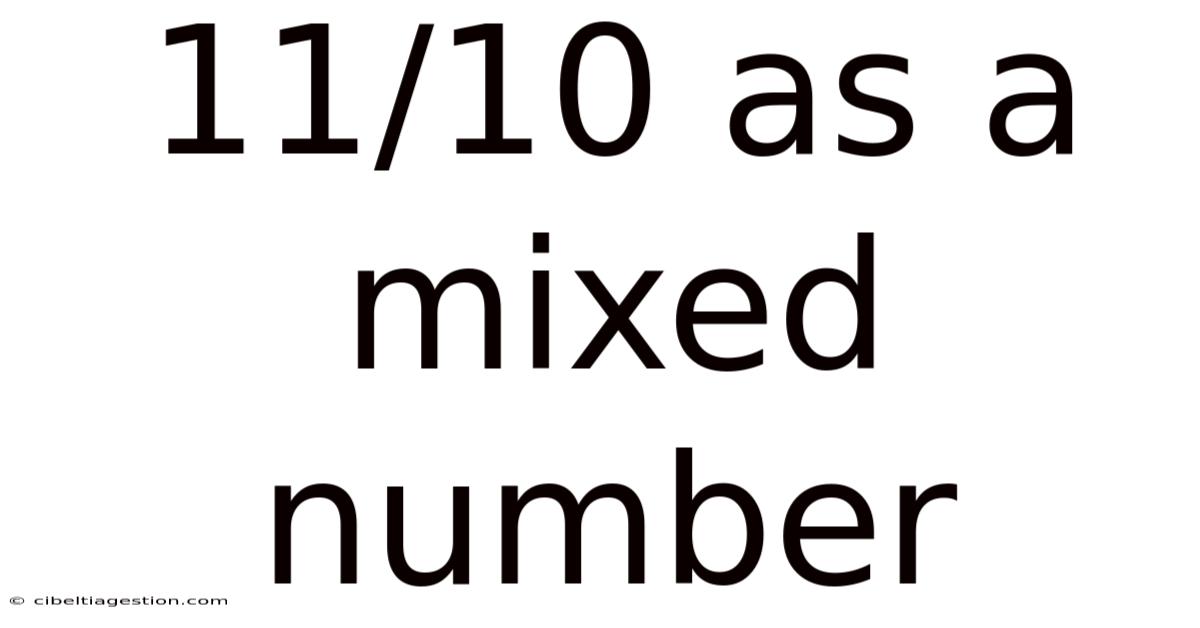
Table of Contents
Understanding 11/10 as a Mixed Number: A Comprehensive Guide
The fraction 11/10 represents a value greater than one. Understanding how to convert this improper fraction into a mixed number is a fundamental skill in mathematics, crucial for various applications from basic arithmetic to more advanced concepts. This comprehensive guide will walk you through the process, explaining the concepts involved and providing a deeper understanding of fractions and their representations. We'll also explore related concepts and answer frequently asked questions, making sure you grasp this important mathematical idea fully.
What is a Mixed Number?
Before diving into the conversion, let's define what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator (the top number) smaller than its denominator (the bottom number). For example, 1 ½, 2 ¾, and 5 ⅛ are all mixed numbers. They represent values larger than one.
What is an Improper Fraction?
Conversely, an improper fraction has a numerator that is greater than or equal to its denominator. Examples include 11/10, 7/4, and 9/9. Improper fractions are another way to represent values greater than or equal to one. Often, converting an improper fraction to a mixed number offers a clearer and more intuitive way to understand the quantity it represents.
Converting 11/10 to a Mixed Number: A Step-by-Step Guide
Converting 11/10 to a mixed number involves dividing the numerator (11) by the denominator (10).
Step 1: Perform the Division
Divide the numerator (11) by the denominator (10). This gives us:
11 ÷ 10 = 1 with a remainder of 1
Step 2: Identify the Whole Number
The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 1.
Step 3: Identify the Fraction
The remainder (the number left over after the division) becomes the numerator of the fraction part of the mixed number. The denominator remains the same as the original fraction's denominator. So, our remainder is 1, and the denominator remains 10. This gives us the fraction 1/10.
Step 4: Combine the Whole Number and the Fraction
Combine the whole number (1) and the fraction (1/10) to form the mixed number: 1 1/10
Therefore, 11/10 expressed as a mixed number is 1 1/10.
Visualizing the Conversion
Imagine you have 11 slices of pizza, and each pizza is cut into 10 slices. You can assemble a whole pizza using 10 slices, leaving you with one slice remaining. This represents one whole pizza (1) and one-tenth of a pizza (1/10), perfectly illustrating the mixed number 1 1/10.
The Mathematical Principle Behind the Conversion
The conversion from an improper fraction to a mixed number is based on the fundamental principle of dividing a larger quantity into smaller, manageable units. It's a way of expressing the same quantity in a different, often more user-friendly format. The process essentially separates the whole units from the remaining fractional part.
Converting Other Improper Fractions to Mixed Numbers
The method described above can be applied to any improper fraction. Let's look at a few more examples:
-
17/5: 17 ÷ 5 = 3 with a remainder of 2. Therefore, 17/5 = 3 2/5
-
23/4: 23 ÷ 4 = 5 with a remainder of 3. Therefore, 23/4 = 5 3/4
-
9/2: 9 ÷ 2 = 4 with a remainder of 1. Therefore, 9/2 = 4 1/2
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand how to convert a mixed number back into an improper fraction. This is often necessary when performing calculations involving mixed numbers. The process is as follows:
Step 1: Multiply the whole number by the denominator.
Step 2: Add the numerator to the result from Step 1.
Step 3: Place the result from Step 2 over the original denominator.
Let's use our example of 1 1/10:
-
Multiply the whole number (1) by the denominator (10): 1 * 10 = 10
-
Add the numerator (1) to the result: 10 + 1 = 11
-
Place the result (11) over the original denominator (10): 11/10
This confirms that our conversion from 11/10 to 1 1/10 is correct.
Applications of Mixed Numbers
Understanding and using mixed numbers is essential in various real-world situations and mathematical contexts:
-
Measurement: Expressing lengths, weights, and volumes often involves mixed numbers (e.g., 2 ½ inches, 3 ¼ pounds).
-
Cooking: Recipes frequently use mixed numbers to specify ingredient quantities (e.g., 1 ½ cups of flour).
-
Construction: Measurements in construction projects commonly involve mixed numbers for precision.
-
Time: Time is often expressed using mixed numbers (e.g., 1 ¾ hours).
-
Algebra and beyond: The ability to work with mixed numbers smoothly underpins more advanced mathematical concepts.
Frequently Asked Questions (FAQs)
Q1: What if the remainder is zero after the division?
A1: If the remainder is zero, it means the original fraction was already a whole number. For example, 10/10 = 1. There is no fractional part in the mixed number representation.
Q2: Can I simplify the fraction part of the mixed number?
A2: Yes, always simplify the fraction part of the mixed number to its lowest terms. For example, if you had 2 4/6, you would simplify the fraction to 2 2/3.
Q3: Why is it important to learn about mixed numbers?
A3: Mixed numbers provide a more intuitive and practical way to represent quantities greater than one in many real-world scenarios. They make calculations easier to visualize and understand, particularly when dealing with measurement and practical applications. Furthermore, a solid understanding of mixed numbers is fundamental to mastering more advanced mathematical concepts.
Q4: What if I have a negative improper fraction?
A4: The process remains the same, except the resulting mixed number will also be negative. For example, -11/10 becomes -1 1/10.
Conclusion
Converting an improper fraction like 11/10 to a mixed number, which in this case is 1 1/10, is a crucial skill in mathematics. This process not only involves simple division but also highlights the relationship between different representations of quantities. Understanding this conversion is vital for tackling more complex mathematical problems and for interpreting real-world measurements and quantities in a clear and meaningful way. Mastering this concept will significantly enhance your mathematical skills and provide a strong foundation for future learning. Remember to always simplify your fractional part and to utilize the knowledge gained to confidently solve various problems involving fractions and mixed numbers.
Latest Posts
Latest Posts
-
Electronic Geometry Vs Molecular Geometry
Sep 14, 2025
-
What Is A Pastoral Society
Sep 14, 2025
-
1 85m In Feet And Inches
Sep 14, 2025
-
What Is Allure Of Fear
Sep 14, 2025
-
How Many Inches Is 18cm
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 11/10 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.