12 15 3 6 4
cibeltiagestion
Sep 10, 2025 · 5 min read
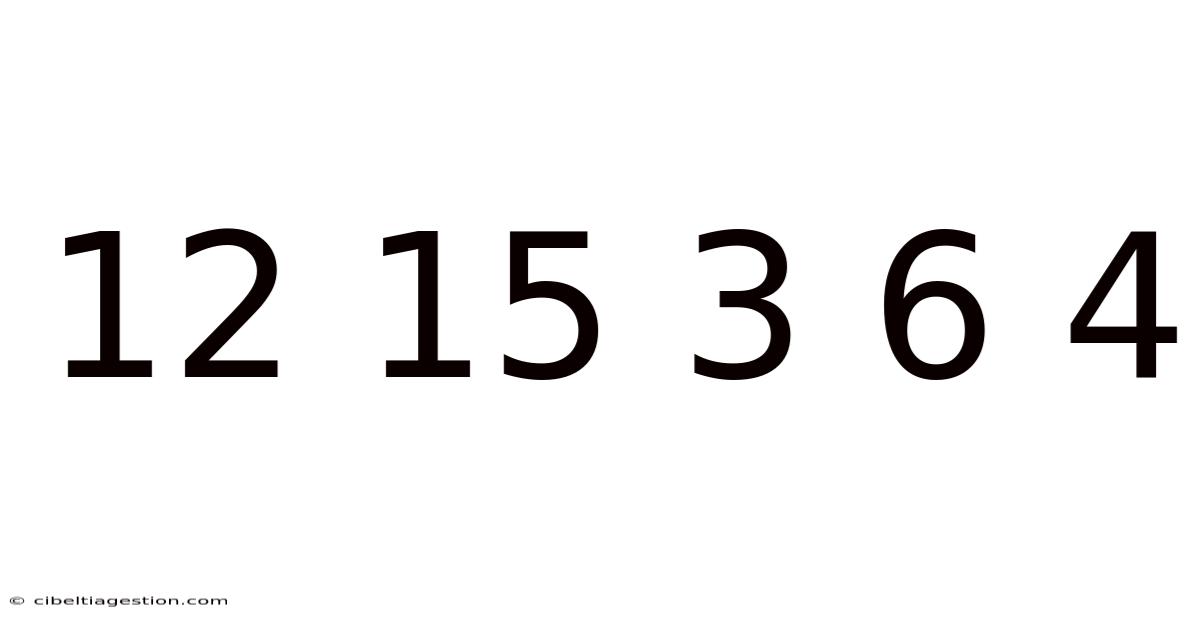
Table of Contents
Decoding the Sequence: Unveiling the Mysteries Behind 12 15 3 6 4
This article delves into the intriguing numerical sequence: 12, 15, 3, 6, 4. At first glance, it appears random. However, upon closer inspection, we can uncover several potential patterns and underlying mathematical principles. This exploration will go beyond simply finding a solution, aiming to demonstrate multiple approaches and highlight the importance of creative problem-solving in mathematics. We'll explore different perspectives, from simple arithmetic operations to more complex mathematical concepts, showcasing how seemingly random sequences can reveal hidden structures and connections.
Introduction: The Allure of Numerical Sequences
Numerical sequences, like 12, 15, 3, 6, 4, have fascinated mathematicians and puzzle enthusiasts for centuries. These sequences often hold hidden patterns, requiring careful observation and creative thinking to decipher. The beauty lies not just in finding a solution but in the process of uncovering the logic behind the arrangement. This particular sequence, while seemingly simple, offers a fertile ground for exploring different mathematical approaches and developing critical thinking skills. We’ll explore various potential interpretations, highlighting the importance of considering multiple perspectives when tackling such problems.
Possible Interpretations and Approaches:
There's no single "correct" answer to interpreting this sequence. The beauty lies in the exploration of different possibilities. Let's examine a few approaches:
1. Arithmetic Operations: A Basic Approach
One straightforward approach is to look for simple arithmetic relationships between consecutive numbers. Let's analyze the differences:
- 15 - 12 = 3
- 3 - 15 = -12
- 6 - 3 = 3
- 4 - 6 = -2
This approach doesn't immediately reveal a consistent pattern. However, let’s explore other arithmetic combinations. Perhaps we can look at sums, products, or even divisions. This illustrates that even simple arithmetic operations can sometimes yield unexpected results, necessitating a broader exploration.
2. Exploring Modular Arithmetic:
Modular arithmetic, where numbers "wrap around" after reaching a certain value (the modulus), could provide a framework. Let's try different moduli:
- Modulus 3: 12 mod 3 = 0, 15 mod 3 = 0, 3 mod 3 = 0, 6 mod 3 = 0, 4 mod 3 = 1. This doesn't immediately reveal a pattern.
- Modulus 5: 12 mod 5 = 2, 15 mod 5 = 0, 3 mod 5 = 3, 6 mod 5 = 1, 4 mod 5 = 4. Again, no obvious pattern emerges.
While modular arithmetic doesn’t immediately provide a clear solution for this specific sequence, it highlights the value of exploring alternative mathematical frameworks in problem-solving. The lack of an obvious pattern with these moduli doesn’t invalidate this approach, simply suggesting the sequence might not be directly governed by a simple modular relationship.
3. Prime Factorization and Number Theory:
Let’s examine the prime factorization of each number:
- 12 = 2² x 3
- 15 = 3 x 5
- 3 = 3
- 6 = 2 x 3
- 4 = 2²
Looking at the prime factors, we don’t immediately observe a consistent pattern. However, this approach could be valuable if combined with other techniques. For instance, we could explore the frequency of prime factors or the relationships between the exponents in the prime factorizations. This demonstrates the potential of combining different mathematical concepts to analyze numerical sequences.
4. Geometric Progressions and Other Advanced Concepts:
While the sequence doesn't appear to follow a simple arithmetic or geometric progression, more advanced mathematical concepts could potentially provide a framework. For instance, we could explore concepts like Fibonacci-like sequences (where each term is a sum of previous terms, but not necessarily the two immediately preceding ones), recursive relationships, or even concepts from abstract algebra. However, these more advanced approaches often require additional information or assumptions about the sequence's underlying structure.
5. Considering the Sequence as Part of a Larger Set:
It’s crucial to consider the context. Is this sequence a complete set, or just a fragment of a larger, more complex sequence? If we consider it a fragment, the possibilities expand significantly. The sequence might be part of a periodic function, a chaotic sequence, or a sequence with properties only apparent when viewed in a broader context. This emphasizes the importance of considering the potential incompleteness of the available data when analyzing numerical patterns.
6. External Context or Hidden Clues:
Without additional information about the origin or intended meaning of the sequence, it’s difficult to definitively decipher its structure. The numbers might represent something entirely outside of pure mathematical relationships. For example, they could represent codes, dates, locations, or elements within a larger puzzle or game. This highlights the limitations of purely mathematical approaches when confronted with sequences lacking clear context.
Developing a Framework for Analysis:
Analyzing numerical sequences like this involves a systematic approach:
- Observation: Carefully examine the numbers, looking for obvious patterns (arithmetic progressions, geometric progressions, etc.).
- Differencing: Calculate the differences between consecutive numbers. Look for patterns in the differences themselves.
- Ratio Analysis: Compute the ratios between consecutive numbers. Examine these ratios for patterns.
- Prime Factorization: Analyze the prime factorization of each number. Look for common factors or patterns in the exponents.
- Modular Arithmetic: Explore different moduli to see if any patterns emerge when numbers are reduced modulo a specific value.
- Advanced Techniques: Consider more sophisticated mathematical concepts if simpler approaches fail.
Conclusion: The Power of Exploration and Critical Thinking
The sequence 12, 15, 3, 6, 4 presents a fascinating challenge. While we haven't found a single definitive solution, the exploration process itself has highlighted several important points. The absence of an immediately obvious pattern underscores the necessity of exploring various mathematical approaches, employing creativity and critical thinking. The problem illustrates that multiple interpretations can be valid depending on the assumptions made and the context provided. Furthermore, it emphasizes the importance of considering the possibility of the sequence being a fragment of a larger whole. This exercise serves as a valuable reminder of the multifaceted nature of mathematics and the rewarding process of uncovering hidden structures within seemingly random sequences. The true value lies not just in finding an answer, but in the journey of exploration and the development of analytical skills.
Latest Posts
Latest Posts
-
Symbols That Represent Emily Dickinson
Sep 10, 2025
-
What Is Value Of Y
Sep 10, 2025
-
When Naming Haircolor Products Manufacturers
Sep 10, 2025
-
Gnome Home Breakout Edu Answers
Sep 10, 2025
-
Ja Biztown Mayor Speech Ideas
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 12 15 3 6 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.