14 Z 3 14z 21
cibeltiagestion
Sep 09, 2025 · 6 min read
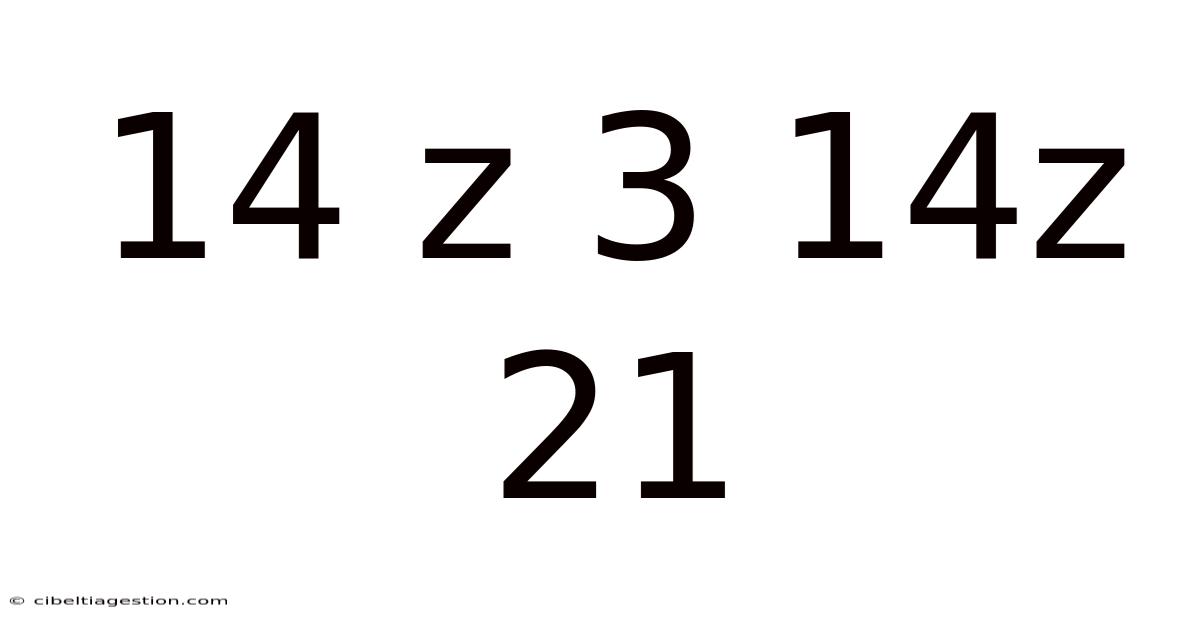
Table of Contents
Decoding the Mystery: 14z 3 14z 21 – A Deep Dive into Mathematical Puzzles and Problem Solving
This article explores the enigmatic sequence "14z 3 14z 21," delving into its potential meanings and the broader context of mathematical puzzles and problem-solving techniques. We'll examine various approaches to deciphering this sequence, considering its structure, potential patterns, and the importance of logical reasoning in uncovering solutions. This seemingly simple sequence opens a door to a world of mathematical exploration, highlighting the beauty and challenge of finding hidden structures within seemingly random data. We'll investigate the importance of pattern recognition, deductive reasoning, and even creative thinking in solving such puzzles.
Understanding the Challenge: What Makes "14z 3 14z 21" Intriguing?
The sequence "14z 3 14z 21" presents a unique challenge because it combines numerical and alphabetical characters. This immediately suggests that a simple arithmetic progression is unlikely. The presence of the letter "z" further complicates matters, hinting at a more complex system or code at play. To solve this, we must move beyond basic arithmetic and explore more sophisticated methods of pattern recognition and code-breaking. The puzzle encourages us to think critically about the relationship between numbers and letters, and how these elements might interact within a specific system.
Potential Approaches: Unraveling the Puzzle
Several approaches can be employed to decipher this sequence. We will explore some of the most promising strategies:
1. Analyzing the Numerical Components:
Let's start by looking at the numbers: 14, 3, 14, 21. Immediately, we notice that 14 appears twice. This repetition is a significant clue, suggesting a potential cycle or a repeating element in the underlying pattern. The differences between the numbers are also noteworthy: 14 - 3 = 11, and 21 - 14 = 7. The lack of an obvious arithmetic progression indicates a more intricate relationship. Could these differences themselves be part of a pattern? Perhaps the sequence operates on different intervals or utilizes a modulo operation.
2. The Role of the Letter "z":
The inclusion of "z" necessitates a deeper investigation. We can consider several possibilities:
- Positional Value: "z" could represent a specific position within a sequence or system. In the English alphabet, "z" is the 26th letter. Is this number relevant? Does it interact with the numerical components in some way?
- Conversion to Numbers: We could try converting "z" to its numerical equivalent (26) and reincorporating this into the sequence. This would yield a purely numerical sequence: 14, 26, 3, 14, 26, 21. Again, analyzing the differences and exploring potential patterns within this new sequence might reveal clues.
- Operational Symbol: The "z" might represent a specific mathematical operation, such as addition, subtraction, multiplication, or a more complex function.
3. Exploring Alternative Number Systems:
The puzzle might be designed using an alternative number system, such as binary, hexadecimal, or even a custom-designed system. If the puzzle is based on a different number system, converting the numbers to base 10 (our standard decimal system) could be a crucial step in uncovering the hidden patterns.
4. Consideration of Mathematical Functions:
The sequence might be related to a specific mathematical function. This could involve trigonometric functions, logarithmic functions, or even more advanced concepts from algebra or calculus. A careful examination of the numerical values and their relationships may reveal a hidden function that generates the sequence.
5. The Importance of Context:
If this sequence appeared within a larger context – for instance, as part of a larger code, a riddle, or a mathematical problem – the surrounding information could provide crucial clues. Without such context, our analysis must rely on exploring the inherent mathematical possibilities.
Deeper Dive into Possible Solutions
Let's consider a few theoretical approaches in more detail:
Hypothetical Scenario 1: A Cyclic Pattern with Modular Arithmetic
The repeated appearance of "14" suggests a cyclical element. Let's assume the sequence operates within a specific modulo. For example, if the sequence operates modulo 11 (since 14 - 3 = 11), then 14 could be considered equivalent to 3 (14 % 11 = 3). This reduces the sequence to 3, 3, 3, 10 (21 % 11 = 10), suggesting a potential, albeit still elusive, pattern.
Hypothetical Scenario 2: A Cipher or Code
The "z" could be part of a simple substitution cipher. Perhaps each number represents a position within a limited alphabet or a specific set of symbols. The "z" could act as a separator or marker within this cipher. Cracking this cipher would require identifying the underlying mapping between numbers and symbols.
Hypothetical Scenario 3: A Combination of Techniques
The most likely solution probably involves a combination of different techniques described above. For example, the "z" might represent a specific operation applied to the numbers, after which a modular arithmetic approach is used. It requires a systematic exploration of various combinations.
Expanding the Understanding: Problem Solving Strategies
The puzzle highlights the importance of several essential problem-solving strategies:
- Pattern Recognition: Identifying repeating elements or predictable sequences is crucial in many mathematical puzzles.
- Deductive Reasoning: Starting with known facts and logically deriving conclusions is a fundamental approach to problem-solving.
- Trial and Error: Experimenting with different approaches and refining hypotheses based on the results is an essential part of the process.
- Creative Thinking: Sometimes, a problem requires thinking outside the box and exploring unconventional solutions.
- Systematic Approach: A structured, organized approach ensures that you explore all relevant possibilities efficiently.
Frequently Asked Questions (FAQ)
Q: Is there a single, definitive answer to this puzzle?
A: Without further context, there isn't a single definitive answer. Multiple interpretations are plausible, each depending on the assumptions made about the underlying system.
Q: What mathematical concepts are relevant to solving this type of puzzle?
A: Several concepts are relevant, including number systems (base conversion), modular arithmetic, cryptography (ciphers and codes), sequences and series, and pattern recognition.
Q: How can I improve my problem-solving skills in mathematics?
A: Practice is key! Solve a wide range of puzzles and problems, focusing on developing your analytical thinking and pattern-recognition abilities. Learn about different mathematical concepts and techniques.
Conclusion: The Journey of Discovery
The seemingly simple sequence "14z 3 14z 21" demonstrates the complexity and richness inherent in even seemingly simple mathematical puzzles. Solving this kind of problem isn’t just about finding the answer; it’s about honing our problem-solving skills, embracing creative thinking, and appreciating the beauty of mathematical structures. The journey of exploring potential solutions is as valuable as arriving at a definitive answer. Each attempt, each hypothesis tested, contributes to a deeper understanding of the principles of logical reasoning and pattern recognition. The true reward lies in the process of discovery itself. Keep exploring, keep questioning, and keep solving!
Latest Posts
Latest Posts
-
How Much Is One Quart
Sep 10, 2025
-
How Much Is 26 Dimes
Sep 10, 2025
-
A Drop Of 200 Feet
Sep 10, 2025
-
The Flexibility Of The An Prc 152
Sep 10, 2025
-
Global Trade Provides Consumers With
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 14 Z 3 14z 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.