15 18 In Lowest Terms.
cibeltiagestion
Sep 10, 2025 · 5 min read
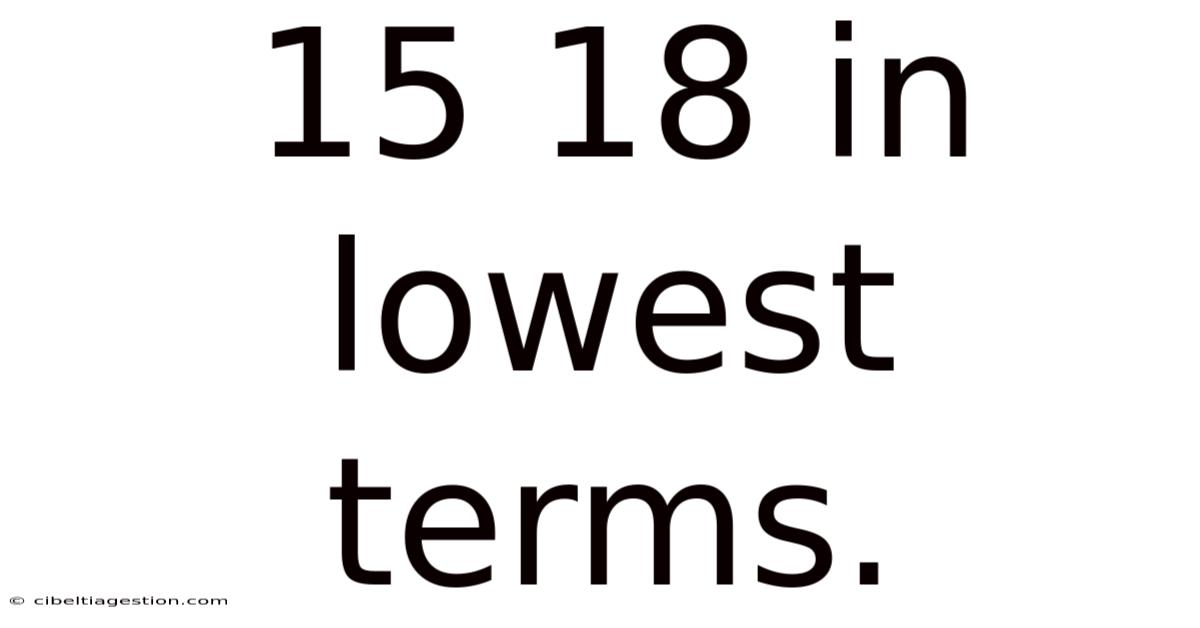
Table of Contents
Simplifying Fractions: A Deep Dive into Reducing 15/18 to Lowest Terms
This article explores the process of simplifying fractions, specifically focusing on reducing the fraction 15/18 to its lowest terms. We'll delve into the fundamental concepts of fractions, greatest common divisors (GCD), and the step-by-step method for simplification, ensuring a comprehensive understanding for learners of all levels. This guide will equip you with the knowledge to tackle similar fraction simplification problems with confidence. Understanding how to reduce fractions is a cornerstone of arithmetic and essential for higher-level mathematical concepts.
Understanding Fractions
Before we embark on simplifying 15/18, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 15/18, 15 is the numerator and 18 is the denominator. This means we have 15 parts out of a possible 18 equal parts.
The Concept of Equivalent Fractions
Equivalent fractions represent the same value, even though they look different. For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent half of a whole. Simplifying a fraction means finding an equivalent fraction where the numerator and denominator are smaller, but the value remains the same. This process is crucial for making fractions easier to understand and work with in calculations.
Finding the Greatest Common Divisor (GCD)
The key to simplifying a fraction is to find the greatest common divisor (GCD), also known as the greatest common factor (GCF), of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Several methods exist for finding the GCD. Let's explore a few:
1. Listing Factors: This method involves listing all the factors of both the numerator and denominator and identifying the largest common factor.
- Factors of 15: 1, 3, 5, 15
- Factors of 18: 1, 2, 3, 6, 9, 18
The common factors are 1 and 3. The greatest common factor is 3.
2. Prime Factorization: This method involves breaking down the numerator and denominator into their prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 15: 3 x 5
- Prime factorization of 18: 2 x 3 x 3 or 2 x 3²
The common prime factor is 3 (appearing once in the factorization of 15 and once in the factorization of 18). Therefore, the GCD is 3.
3. Euclidean Algorithm: This is a more efficient method for larger numbers. The algorithm involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
Let's apply the Euclidean algorithm to 15 and 18:
- 18 ÷ 15 = 1 with a remainder of 3
- 15 ÷ 3 = 5 with a remainder of 0
The last non-zero remainder is 3, so the GCD of 15 and 18 is 3.
Reducing 15/18 to Lowest Terms
Now that we've determined the GCD of 15 and 18 is 3, we can simplify the fraction:
Divide both the numerator and the denominator by the GCD (3):
15 ÷ 3 = 5 18 ÷ 3 = 6
Therefore, 15/18 simplified to its lowest terms is 5/6.
This means that 15/18 and 5/6 represent the same value. 5/6 is a simpler and more manageable representation of the fraction.
Visual Representation
Imagine a pizza cut into 18 equal slices. If you have 15 slices, you have 15/18 of the pizza. Now, imagine grouping those slices into sets of 3. You'll have 5 groups of 3 slices each. Since the whole pizza was originally divided into 18 slices (groups of 3 slices each), that is 6 groups of 3. So, you have 5 out of 6 groups, which represents 5/6 of the pizza. This visual representation helps solidify the understanding of equivalent fractions.
Applications of Fraction Simplification
Simplifying fractions is not just a mathematical exercise; it has practical applications in various fields:
- Cooking and Baking: Recipes often use fractions, and simplifying them makes measurements easier and more precise.
- Construction and Engineering: Calculations in construction and engineering often involve fractions, and simplifying them ensures accuracy and efficiency.
- Finance: Fractions are used extensively in finance, particularly in calculations involving interest rates, percentages, and ratios.
- Data Analysis: When dealing with proportions and percentages in data analysis, simplified fractions provide a clearer picture.
Frequently Asked Questions (FAQ)
-
Q: What if I divide by a number that is not the GCD? A: You'll still get an equivalent fraction, but it won't be in its lowest terms. You'll need to repeat the process using the GCD to fully simplify the fraction.
-
Q: Can a fraction be simplified if the GCD is 1? A: Yes, if the GCD of the numerator and denominator is 1, the fraction is already in its lowest terms. It cannot be simplified further. Such fractions are called irreducible fractions.
-
Q: How do I simplify fractions with larger numbers? A: The Euclidean algorithm or prime factorization are more efficient methods for finding the GCD of larger numbers.
Conclusion
Simplifying fractions is a fundamental skill in mathematics. By understanding the concept of equivalent fractions, the greatest common divisor, and the various methods for finding it, you can confidently reduce any fraction to its lowest terms. The process of simplifying 15/18 to 5/6 demonstrates this clearly. Remember that the simplified fraction represents the same value as the original fraction, but it is easier to work with in calculations and applications. Mastering this skill opens doors to a deeper understanding of more complex mathematical concepts and real-world problem-solving. Practice makes perfect, so continue to work through various fraction simplification problems to solidify your understanding and build your confidence. The ability to simplify fractions is a valuable tool that will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
How Many Cups Is 3oz
Sep 10, 2025
-
69 Degrees Celsius To Fahrenheit
Sep 10, 2025
-
Convert 77 Kilos To Pounds
Sep 10, 2025
-
They Will See In Spanish
Sep 10, 2025
-
1 3 Of 3 Feet
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 15 18 In Lowest Terms. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.