15 Divided By 1 3
cibeltiagestion
Sep 13, 2025 · 6 min read
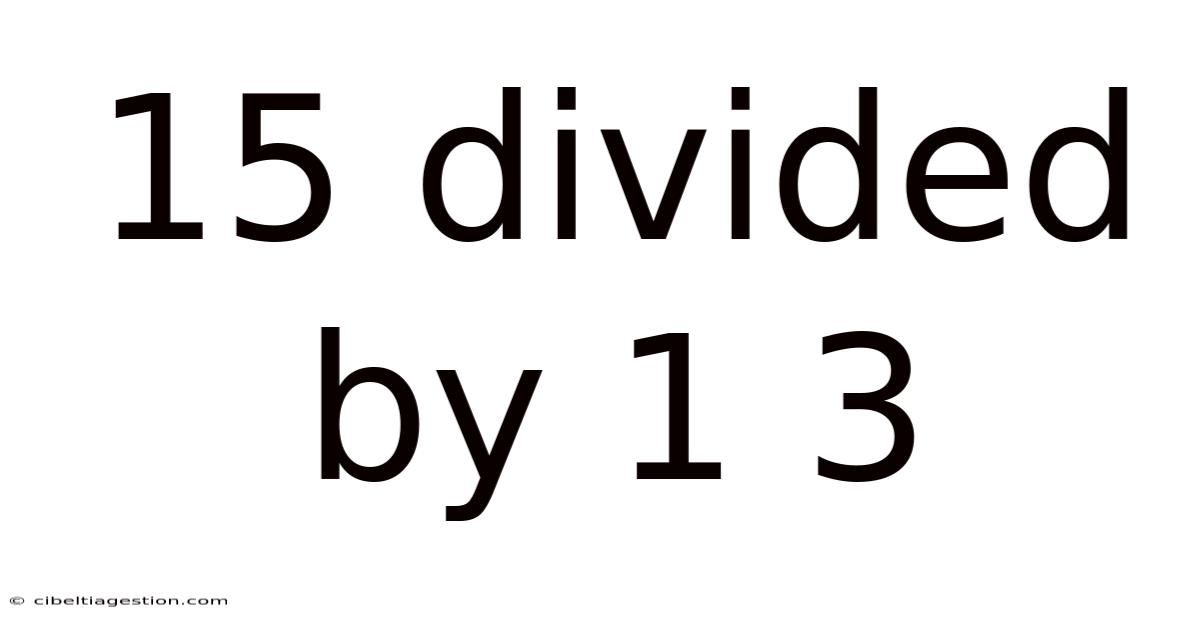
Table of Contents
Unveiling the Mystery: 15 Divided by 1/3
Understanding fractions and division can sometimes feel like navigating a mathematical maze. This article delves into the seemingly simple yet often misunderstood problem of 15 divided by 1/3, providing a comprehensive explanation that moves beyond the answer to illuminate the underlying concepts. We’ll explore various approaches to solving this problem, explaining the "why" behind the calculations and addressing common misconceptions. By the end, you’ll not only know the answer but also possess a deeper understanding of fractional division.
Introduction: Why is this problem tricky?
Many students stumble when faced with division involving fractions. The problem, "15 divided by 1/3," is a perfect example. Intuitively, we might expect a smaller answer since we're dividing. However, the correct answer is significantly larger than 15. This counterintuitive result stems from a fundamental misunderstanding of what division actually represents. Division isn't just about splitting something into smaller parts; it's about determining how many times one quantity fits into another. In this case, we're asking: "How many times does 1/3 fit into 15?"
Understanding Division: A Conceptual Approach
Before diving into the calculations, let's solidify our understanding of division. Consider a simpler problem: 12 divided by 3 (12 ÷ 3). This means, "How many groups of 3 can we make from 12?" The answer is 4. We can visualize this by arranging 12 objects into groups of 3.
Now, let's apply this to our problem: 15 divided by 1/3 (15 ÷ 1/3). We're asking: "How many groups of 1/3 can we make from 15?" This is where the intuition falters. Since 1/3 is a small fraction, many groups of 1/3 will fit into 15.
Method 1: The "Keep, Change, Flip" Method
This is a popular shortcut for dividing fractions. The method involves three steps:
- Keep: Keep the first number (the dividend) as it is. In our case, this remains 15.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second number (the divisor) – also known as finding the reciprocal. The reciprocal of 1/3 is 3/1, or simply 3.
Therefore, the problem becomes: 15 × 3 = 45
This method works because multiplying by the reciprocal is mathematically equivalent to dividing by the original fraction.
Method 2: Visual Representation
We can visualize this problem using a diagram. Imagine a line representing 15 units. Now, divide this line into segments of 1/3 each. How many segments will you have?
Let's break it down:
- Each unit contains three segments of 1/3.
- Since we have 15 units, we have 15 * 3 = 45 segments of 1/3.
This visual approach reinforces the understanding that we are finding how many smaller parts (1/3) fit into a larger whole (15).
Method 3: Converting to Improper Fractions
While the "keep, change, flip" method is convenient, it's helpful to understand the underlying mathematical principle. We can solve this problem by converting the whole number (15) into a fraction: 15/1. The problem then becomes:
(15/1) ÷ (1/3)
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction:
(15/1) × (3/1) = 45/1 = 45
This method clarifies the mathematical process involved, emphasizing the principle of multiplying by the reciprocal.
The Importance of Understanding Reciprocals
The concept of a reciprocal is central to understanding fractional division. The reciprocal of a number is simply 1 divided by that number. For example:
- The reciprocal of 2 is 1/2
- The reciprocal of 5 is 1/5
- The reciprocal of 1/3 is 3/1 (or 3)
- The reciprocal of 2/5 is 5/2
Understanding reciprocals is crucial not only for dividing fractions but also for various other mathematical operations.
Addressing Common Misconceptions
Many students incorrectly attempt to simply divide 15 by 1 and then divide by 3, resulting in an answer of 5. This is wrong because it ignores the fractional nature of the divisor (1/3). Remember, we're determining how many 1/3s fit into 15, not how many 1s fit into 15 and then subsequently dividing by 3. The fractional divisor changes the entire dynamic of the problem.
Another common mistake involves incorrectly flipping the wrong fraction. Remember, it's only the divisor (the number after the division sign) that is flipped, not the dividend (the number before the division sign).
Real-world Applications
Understanding fractional division is essential in various real-world scenarios:
- Cooking: If a recipe calls for 1/3 cup of sugar and you want to triple the recipe, you'd need to calculate 3 x (1/3 cup) = 1 cup. This involves a fractional division (3 ÷ (1/3) = 9 times the recipe).
- Construction: Dividing lengths of materials accurately often involves fractions.
- Sewing: Cutting fabric requires precise calculations with fractions.
- Engineering: Design specifications in engineering commonly utilize fractions.
These real-world examples highlight the practical relevance of mastering fractional division.
Expanding the Concept: Dividing by Fractions Smaller than 1/3
Let's consider dividing 15 by a smaller fraction, say 1/6. Following the same principles:
15 ÷ (1/6) = 15 × (6/1) = 90
Notice that as the divisor becomes smaller (closer to zero), the quotient (the answer) becomes larger. This reinforces the idea that division is about determining how many times one quantity fits into another. If the divisor is very small, a large number of them will fit into the dividend.
A Deeper Dive into the Mathematics: The Multiplicative Inverse
The act of "flipping" a fraction and multiplying is mathematically equivalent to multiplying by the multiplicative inverse. Every non-zero number has a multiplicative inverse, which, when multiplied by the original number, results in 1. The reciprocal and the multiplicative inverse are the same thing. This provides a rigorous mathematical foundation for the "keep, change, flip" method.
Frequently Asked Questions (FAQ)
Q: Why is the answer 45 and not 5?
A: The error in obtaining 5 stems from incorrectly treating the problem as 15 ÷ 1 ÷ 3 instead of 15 ÷ (1/3). The parentheses are crucial in indicating the order of operations. We are dividing 15 by the entire fraction 1/3, not dividing 15 by 1 and then by 3 separately.
Q: Can I use a calculator to solve this?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is far more important than simply obtaining the answer using a calculator. The focus should be on grasping the concepts of fractional division and reciprocal multiplication.
Q: What if the dividend was also a fraction?
A: The same principles apply. You would still convert both numbers to fractions, then multiply the first fraction by the reciprocal of the second fraction. For example: (2/5) ÷ (1/3) = (2/5) × (3/1) = 6/5.
Conclusion: Mastering Fractional Division
Mastering fractional division involves more than just memorizing a method; it necessitates a thorough understanding of the fundamental concepts of division and reciprocals. Through both visual and mathematical approaches, we've explored the problem of 15 divided by 1/3, arriving at the correct answer of 45. Remember, the key lies not just in getting the answer but in understanding why the answer is what it is. This deep understanding will serve you well in tackling more complex mathematical problems and in various real-world applications that involve fractions. By understanding the "why" behind the "how," you'll confidently navigate the world of fractions and unlock a deeper appreciation for the elegance of mathematics.
Latest Posts
Latest Posts
-
Lewis Structure Of Hypochlorite Ion
Sep 14, 2025
-
Natural Resources Northeast United States
Sep 14, 2025
-
When Are Atoms Most Stable
Sep 14, 2025
-
Which Image Shows A Rotation
Sep 14, 2025
-
24 Oz How Many Pounds
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 15 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.