17/3 As A Mixed Number
cibeltiagestion
Sep 16, 2025 · 5 min read
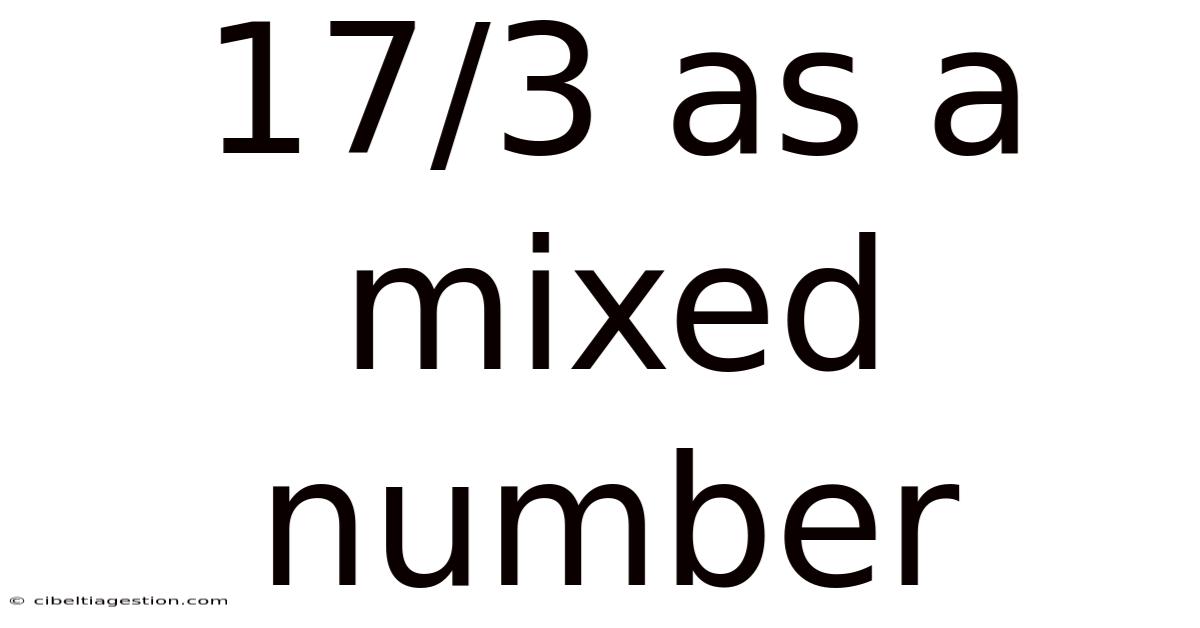
Table of Contents
Understanding 17/3 as a Mixed Number: A Comprehensive Guide
The fraction 17/3 represents seventeen-thirds. While perfectly valid in its improper fraction form, understanding how to convert it into a mixed number is crucial for various mathematical operations and a deeper grasp of fractional concepts. This comprehensive guide will explore the conversion process, delve into the underlying mathematical principles, and address frequently asked questions about mixed numbers and improper fractions. We'll also explore practical applications and the significance of understanding this conversion.
Introduction to Fractions and Mixed Numbers
Before diving into the specifics of 17/3, let's briefly review the fundamental concepts of fractions and mixed numbers. A fraction represents a part of a whole. It's composed of two parts: the numerator (the top number) indicating the number of parts you have, and the denominator (the bottom number) indicating the total number of equal parts the whole is divided into.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 17/3, 5/5, 22/7). In contrast, a proper fraction has a numerator smaller than the denominator (e.g., 1/2, 3/4, 5/8).
A mixed number combines a whole number and a proper fraction (e.g., 5 2/3, 1 1/4, 3 7/8). It represents a quantity that is greater than one. Understanding the relationship between improper fractions and mixed numbers is essential for performing various calculations efficiently and interpreting results meaningfully.
Converting 17/3 into a Mixed Number: A Step-by-Step Guide
The process of converting an improper fraction like 17/3 into a mixed number involves dividing the numerator by the denominator. Here's how it works:
-
Divide the Numerator by the Denominator: Divide 17 by 3.
17 ÷ 3 = 5 with a remainder of 2.
-
Identify the Whole Number: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 5.
-
Identify the Remainder: The remainder from the division becomes the numerator of the fractional part of the mixed number. Here, the remainder is 2.
-
Keep the Original Denominator: The denominator of the fractional part remains the same as the denominator of the original improper fraction. This remains as 3.
-
Combine the Whole Number and the Fraction: Put the whole number and the fraction together to form the mixed number.
Therefore, 17/3 as a mixed number is 5 2/3.
Visual Representation of 17/3
Imagine you have 17 equally sized pieces of a pizza. If each pizza is cut into 3 slices, you can make 5 whole pizzas (5 x 3 = 15 slices) and you'll have 2 slices left over. This visually represents the 5 whole pizzas and the remaining 2/3 of a pizza, confirming that 17/3 is equivalent to 5 2/3.
The Mathematical Principle Behind the Conversion
The conversion process is based on the fundamental principle of equivalent fractions. When we divide 17 by 3, we are essentially finding how many times 3 fits into 17. It fits 5 times completely (giving us 5 whole units), with 2 parts remaining. These 2 remaining parts, out of the original 3 parts that make a whole, represent the fraction 2/3.
This can be expressed mathematically as follows:
17/3 = (3 x 5 + 2) / 3 = (15 + 2) / 3 = 15/3 + 2/3 = 5 + 2/3 = 5 2/3
This demonstrates that we're not changing the value of the fraction; we're just expressing it in a different, often more understandable, form.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process – converting a mixed number back to an improper fraction. Let's take our example, 5 2/3:
-
Multiply the whole number by the denominator: 5 x 3 = 15
-
Add the numerator: 15 + 2 = 17
-
Keep the denominator: The denominator remains 3.
Therefore, the improper fraction equivalent to 5 2/3 is 17/3.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in everyday life and various fields:
-
Cooking and Baking: Recipes often call for quantities expressed as mixed numbers (e.g., 2 1/2 cups of flour).
-
Measurement: Measurements of length, weight, and volume are commonly represented using mixed numbers (e.g., 5 3/4 inches).
-
Construction and Engineering: Precise measurements in construction and engineering require the use of mixed numbers to ensure accuracy.
-
Data Analysis and Statistics: Mixed numbers might appear in datasets representing averages or proportions.
Frequently Asked Questions (FAQ)
Q1: Why use mixed numbers instead of improper fractions?
A1: Mixed numbers often provide a more intuitive understanding of quantities, especially when dealing with whole units and parts. For instance, saying "5 2/3 pizzas" is clearer than "17/3 pizzas" for most people. However, improper fractions are essential for certain mathematical operations.
Q2: Can all improper fractions be converted to mixed numbers?
A2: Yes, all improper fractions can be converted into mixed numbers, as long as the denominator is not zero (division by zero is undefined).
Q3: Are mixed numbers and improper fractions equivalent?
A3: Yes, a mixed number and its corresponding improper fraction represent the same value. They are simply different ways of expressing the same quantity.
Q4: Which form is better to use, mixed numbers or improper fractions?
A4: The choice depends on the context. Mixed numbers are often preferred for representing quantities in everyday situations, while improper fractions are more suitable for calculations, especially those involving multiplication and division of fractions.
Q5: How do I compare mixed numbers?
A5: To compare mixed numbers, first compare the whole number parts. If the whole number parts are different, the number with the larger whole number is greater. If the whole number parts are the same, compare the fractional parts.
Conclusion
Understanding the conversion between improper fractions and mixed numbers is a fundamental skill in mathematics. The ability to seamlessly switch between these forms is crucial for solving problems involving fractions and grasping the true meaning of fractional quantities. The conversion process is straightforward, based on simple division and the understanding of remainders. Remember, both the improper fraction (17/3) and the mixed number (5 2/3) represent the same quantity; the choice of which form to use depends on the specific context and desired clarity. By mastering this concept, you'll build a stronger foundation in mathematics and be better equipped to tackle more complex problems involving fractions in various applications.
Latest Posts
Latest Posts
-
Button With Triangle Above Rectangle
Sep 16, 2025
-
Whats The Capital Of Venezuela
Sep 16, 2025
-
How Much Is 120 Minutes
Sep 16, 2025
-
All Physicians Take Money Mnemonic
Sep 16, 2025
-
E Value Of Boric Acid
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 17/3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.