2 1/2 Divided By 1/2
cibeltiagestion
Sep 13, 2025 · 6 min read
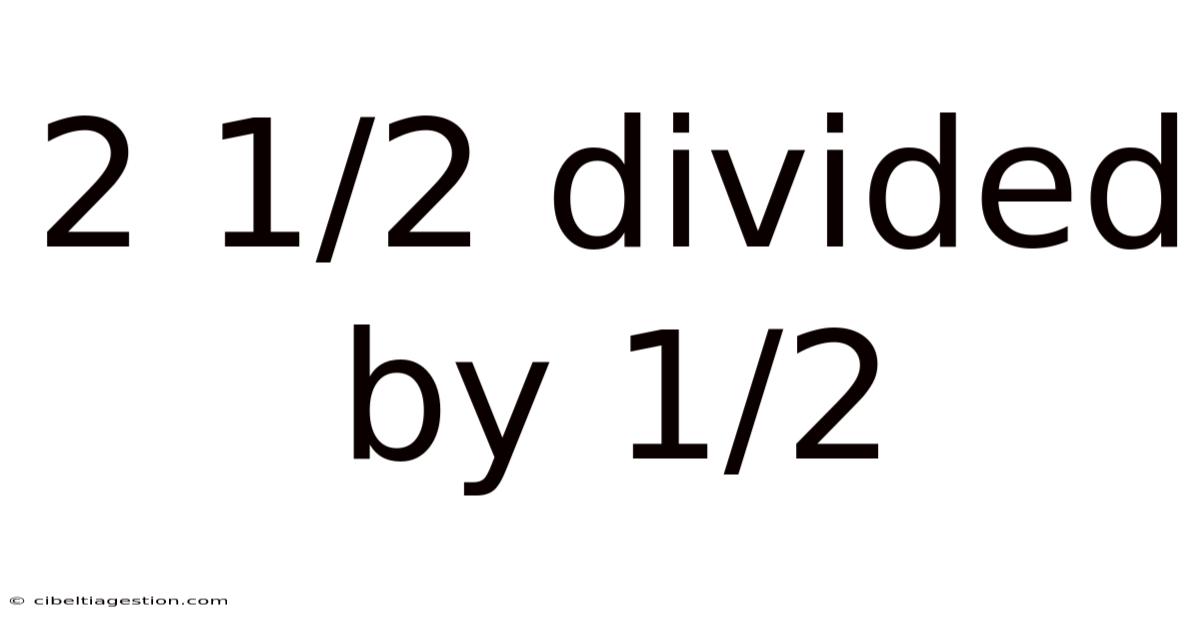
Table of Contents
2 1/2 Divided by 1/2: A Deep Dive into Fraction Division
Dividing fractions can seem daunting, especially when mixed numbers like 2 1/2 are involved. But fear not! This comprehensive guide will walk you through the process of solving 2 1/2 divided by 1/2, explaining the underlying principles and offering various approaches to reach the correct answer. We'll explore the intricacies of fraction division, providing a clear and intuitive understanding applicable to a wide range of similar problems. This article is perfect for students struggling with fraction division, teachers looking for supplementary materials, or anyone who wants to solidify their understanding of this fundamental mathematical concept.
Understanding the Fundamentals of Fraction Division
Before diving into the specific problem of 2 1/2 divided by 1/2, let's review the basics of fraction division. The core principle is to invert the second fraction (the divisor) and multiply. This seemingly simple rule is rooted in the reciprocal relationship between multiplication and division.
Remember that the reciprocal of a fraction is obtained by swapping its numerator and denominator. For instance, the reciprocal of 1/2 is 2/1 (or simply 2).
So, when we divide any fraction (a/b) by another fraction (c/d), the operation translates to:
(a/b) ÷ (c/d) = (a/b) x (d/c)
This means we multiply the first fraction by the reciprocal of the second fraction. This fundamental principle is the cornerstone of solving any fraction division problem.
Solving 2 1/2 Divided by 1/2: Step-by-Step Guide
Now, let's tackle the problem at hand: 2 1/2 ÷ 1/2. We'll break down the solution into manageable steps.
Step 1: Convert the Mixed Number to an Improper Fraction
The first step is to convert the mixed number 2 1/2 into an improper fraction. A mixed number combines a whole number and a fraction. To convert it, we multiply the whole number by the denominator of the fraction, add the numerator, and keep the same denominator.
2 1/2 = (2 x 2) + 1 / 2 = 5/2
Now our problem becomes: 5/2 ÷ 1/2
Step 2: Invert the Second Fraction (the Divisor) and Multiply
Following the rule of fraction division, we invert the second fraction (1/2) to get its reciprocal, which is 2/1. Then, we change the division sign to a multiplication sign:
5/2 ÷ 1/2 = 5/2 x 2/1
Step 3: Perform the Multiplication
Now, we perform the multiplication of the fractions. We multiply the numerators together and the denominators together:
(5 x 2) / (2 x 1) = 10/2
Step 4: Simplify the Resulting Fraction
Finally, we simplify the resulting fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 2 in this case:
10/2 = 5
Therefore, 2 1/2 divided by 1/2 equals 5.
Visualizing the Division: A Practical Approach
Understanding fraction division conceptually can be greatly enhanced through visualization. Imagine you have 2 1/2 pizzas, and you want to divide them into servings of 1/2 pizza each. How many servings will you have?
If you divide each whole pizza into two halves, you'll have four halves from the two whole pizzas. The remaining half pizza adds another half, giving you a total of five halves. This visually confirms our calculated answer of 5.
Different Methods for Solving Fraction Division
While the method outlined above is the most common, there are other approaches to solving 2 1/2 ÷ 1/2. Let's explore some alternatives:
Method 1: Using Decimal Representation
We can convert the fractions to decimals and perform the division.
2 1/2 = 2.5
1/2 = 0.5
2.5 ÷ 0.5 = 5
This method is quicker for simple fractions but might not be as efficient for complex fractions.
Method 2: Thinking in Terms of Halves
We can interpret the problem as "How many halves are there in 2 1/2?". Since there are two halves in one whole pizza, there are four halves in two whole pizzas, plus an additional half, making a total of five halves. This intuitive approach provides a solid understanding of the underlying concept.
Method 3: Common Denominator Approach (Less Efficient for this Example)
While not the most efficient for this specific problem, it's helpful to understand this method for more complex cases. You could find a common denominator for both fractions before dividing. This method involves rewriting the fractions with a common denominator before dividing the numerators. However, this method becomes more complex with larger numbers and is generally less efficient than inverting and multiplying for most problems.
The Importance of Understanding Fraction Division
Mastering fraction division is crucial for building a solid foundation in mathematics. It's a fundamental concept that extends to various areas like:
- Algebra: Solving equations involving fractions.
- Geometry: Calculating areas and volumes of shapes.
- Real-world applications: Dividing recipes, measuring ingredients, and many other practical scenarios.
Frequently Asked Questions (FAQ)
Q: Why do we invert and multiply when dividing fractions?
A: Inverting and multiplying is a shortcut that stems from the definition of division as the inverse operation of multiplication. Dividing by a fraction is the same as multiplying by its reciprocal.
Q: Can I use a calculator to solve fraction division problems?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is essential for solving more complex problems and for building a strong mathematical foundation.
Q: What if the divisor is a whole number?
A: A whole number can be expressed as a fraction with a denominator of 1. For example, 5 can be written as 5/1. You can then apply the same invert and multiply method.
Q: What happens if the result is an improper fraction?
A: If the result is an improper fraction (where the numerator is larger than the denominator), you can convert it to a mixed number for easier interpretation.
Conclusion: Mastering Fraction Division
Solving 2 1/2 divided by 1/2, as we've demonstrated, is straightforward once you grasp the core principles of fraction division. Remember the crucial step of converting mixed numbers to improper fractions before applying the "invert and multiply" rule. By understanding the various methods and practicing regularly, you'll build confidence and proficiency in tackling even more complex fraction division problems. The ability to confidently perform fraction division will significantly enhance your mathematical skills and open doors to more advanced concepts. Embrace the challenge, practice diligently, and you'll master this essential skill in no time!
Latest Posts
Latest Posts
-
How Many Inches Is 7ft
Sep 13, 2025
-
Chromosomes 1 44 In A Human
Sep 13, 2025
-
Actual Dimensions Of A 2x6
Sep 13, 2025
-
Streams And Rivers Distinguishing Characteristics
Sep 13, 2025
-
Is Koh A Strong Base
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2 1/2 Divided By 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.