2 3/7 - 5 6/7
cibeltiagestion
Sep 11, 2025 · 5 min read
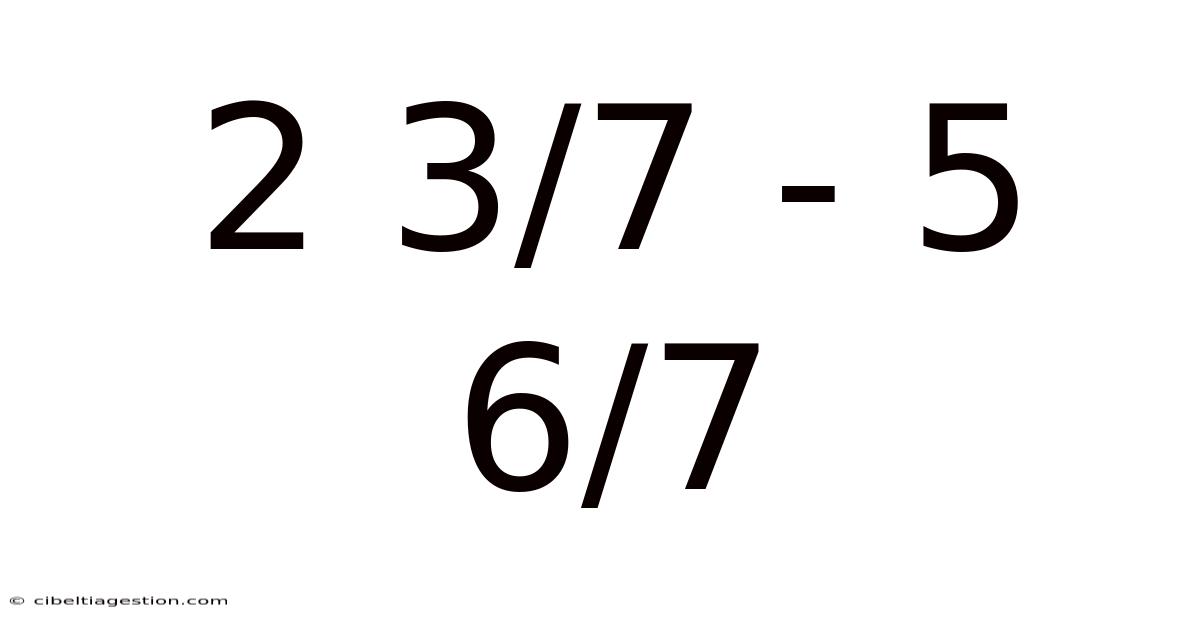
Table of Contents
Solving Subtraction Problems with Mixed Fractions: A Deep Dive into 2 3/7 - 5 6/7
Subtracting mixed fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This article will guide you through solving the problem 2 3/7 - 5 6/7, explaining each step in detail and providing valuable insights into the underlying mathematical principles. We'll explore different approaches, address common pitfalls, and build a strong foundation for tackling similar problems. This comprehensive guide is perfect for students, teachers, and anyone looking to improve their skills in arithmetic.
Understanding Mixed Fractions
Before we delve into the subtraction problem, let's solidify our understanding of mixed fractions. A mixed fraction combines a whole number and a proper fraction. For example, 2 3/7 represents two whole units and an additional 3/7 of a unit. Understanding this representation is crucial for successfully manipulating mixed fractions in mathematical operations.
The Challenge: 2 3/7 - 5 6/7
Our specific problem is to subtract 5 6/7 from 2 3/7. Notice immediately that we are attempting to subtract a larger number from a smaller number. This requires a crucial step that many students initially struggle with: borrowing.
Method 1: Converting to Improper Fractions
One common and effective approach involves converting both mixed fractions into improper fractions. An improper fraction has a numerator larger than or equal to its denominator. This conversion simplifies the subtraction process.
Step 1: Convert 2 3/7 to an improper fraction:
To convert 2 3/7, we multiply the whole number (2) by the denominator (7) and add the numerator (3). This result (2 * 7 + 3 = 17) becomes the new numerator, while the denominator remains the same (7). Therefore, 2 3/7 becomes 17/7.
Step 2: Convert 5 6/7 to an improper fraction:
Similarly, for 5 6/7, we calculate (5 * 7 + 6 = 41), resulting in the improper fraction 41/7.
Step 3: Perform the Subtraction:
Now we have a straightforward subtraction problem with improper fractions: 17/7 - 41/7. Since the denominators are the same, we simply subtract the numerators: 17 - 41 = -24. The denominator remains unchanged. This gives us -24/7.
Step 4: Convert back to a Mixed Fraction (optional):
The result -24/7 is an improper fraction. To express it as a mixed fraction, we divide the numerator (-24) by the denominator (7). -24 divided by 7 is -3 with a remainder of -3. Therefore, -24/7 can be written as -3 3/7.
Method 2: Borrowing from the Whole Number
Another method involves directly subtracting using the concept of borrowing. Since we can't directly subtract 6/7 from 3/7, we need to borrow from the whole number part.
Step 1: Borrowing:
We borrow 1 from the whole number 2, leaving us with 1. This borrowed 1 is then converted into a fraction with the same denominator as the existing fractions, which is 7/7.
Step 2: Rewrite the Expression:
Our expression now becomes: (1 + 7/7 + 3/7) - 5 6/7 = (1 + 10/7) - 5 6/7
Step 3: Subtraction:
Now we can subtract the whole numbers: 1 - 5 = -4. Then, we subtract the fractions: 10/7 - 6/7 = 4/7.
Step 4: Combine:
Combining the whole number and the fraction, we get -4 + 4/7 = -4 4/7. Note that this is equivalent to the -24/7 we obtained in Method 1, confirming our work. To see this, convert -4 4/7 to an improper fraction: (-4 * 7) + 4 = -24. So it is -24/7.
Why are the results different in presentation?
Although the methods arrived at -3 3/7 and -4 4/7, both fractions are equivalent to -24/7. The difference lies in the way the improper fraction is converted back to mixed number. In essence, there is an extra -7/7 implied in -4 4/7.
Addressing Common Mistakes
Several common errors can occur when subtracting mixed fractions. Let's address some of these:
-
Forgetting to convert to improper fractions: Trying to subtract directly without converting to improper fractions often leads to incorrect results. Always ensure you have a common denominator before subtracting.
-
Incorrect borrowing: When borrowing from the whole number, make sure you convert the borrowed 1 correctly into a fraction with the correct denominator.
-
Errors in arithmetic: Double-check your addition and subtraction operations to avoid careless mistakes.
-
Ignoring negative signs: Remember that subtracting a larger number from a smaller number will result in a negative answer. Carefully handle negative signs throughout the calculation.
Further Exploration: Mathematical Properties
This problem highlights the significance of understanding fundamental mathematical properties like the additive inverse and the commutative property (for addition). Remember that subtracting a number is equivalent to adding its additive inverse.
Frequently Asked Questions (FAQ)
Q: Can I subtract mixed fractions directly without converting to improper fractions?
A: While possible in some cases, converting to improper fractions is generally recommended for consistency and to avoid potential errors, especially when dealing with more complex problems.
Q: What if the denominators are different?
A: If the denominators are different, you must find the least common denominator (LCD) before subtracting. This involves finding the smallest multiple that both denominators share.
Q: What happens if the result is an improper fraction?
A: An improper fraction should generally be converted back to a mixed fraction for easier interpretation.
Conclusion
Subtracting mixed fractions, even seemingly simple problems like 2 3/7 - 5 6/7, requires careful attention to detail and a clear understanding of the underlying mathematical principles. By mastering the steps outlined in this article – whether converting to improper fractions or using the borrowing method – you'll build confidence and competence in solving a wide range of fraction problems. Remember to check your work and avoid common pitfalls, and you'll find that these operations become much simpler with practice. This thorough explanation equips you to tackle more challenging mixed fraction problems with ease and accuracy.
Latest Posts
Latest Posts
-
8 3 9 Text To Binary
Sep 11, 2025
-
Consumers Express Self Interest When They
Sep 11, 2025
-
Write 47 In Expanded Form
Sep 11, 2025
-
Recharge Is The Transfer Of
Sep 11, 2025
-
Sirius Black Azkaban Prison Number
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 2 3/7 - 5 6/7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.