2 5/8 As A Decimal
cibeltiagestion
Sep 13, 2025 · 6 min read
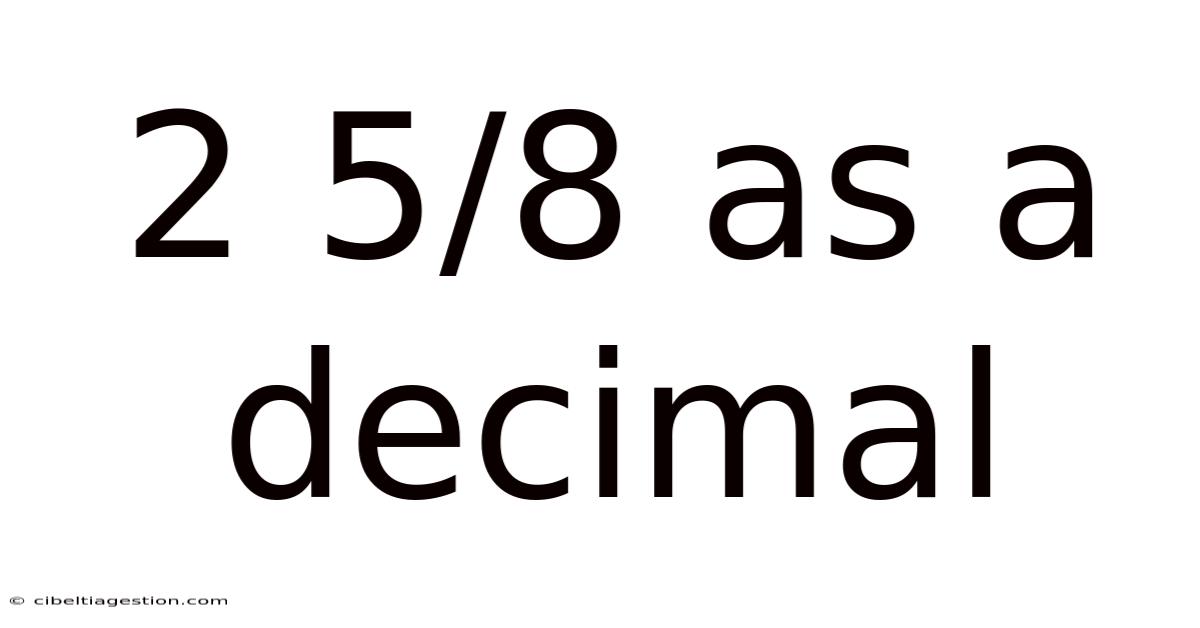
Table of Contents
2 5/8 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to complex scientific problems. This comprehensive guide will explore the conversion of the mixed number 2 5/8 into its decimal equivalent, providing a step-by-step explanation, exploring the underlying principles, and addressing frequently asked questions. Understanding this process will solidify your grasp of fractions and decimals, empowering you to tackle similar conversions with confidence.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's clarify the terminology. A mixed number combines a whole number and a fraction, like 2 5/8. The whole number (2 in this case) represents complete units, while the fraction (5/8) represents a portion of a unit. The fraction itself has a numerator (5, the top number) and a denominator (8, the bottom number). The denominator indicates the total number of equal parts into which a unit is divided, and the numerator specifies how many of those parts are being considered.
Method 1: Converting the Fraction First
This method involves converting the fractional part of the mixed number into a decimal and then adding the whole number. Here's how to convert 2 5/8 to a decimal using this approach:
-
Convert the fraction to a decimal: To convert 5/8 to a decimal, we divide the numerator (5) by the denominator (8): 5 ÷ 8 = 0.625
-
Add the whole number: Now, add the whole number part (2) to the decimal equivalent of the fraction (0.625): 2 + 0.625 = 2.625
Therefore, 2 5/8 as a decimal is 2.625.
Method 2: Converting the Entire Mixed Number Directly
This method involves converting the entire mixed number into an improper fraction first, then dividing to obtain the decimal. This approach offers a slightly different perspective and can be beneficial for understanding the underlying principles.
-
Convert to an improper fraction: To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator. In our case:
(2 * 8) + 5 = 21
The improper fraction becomes 21/8.
-
Divide the numerator by the denominator: Now, divide the numerator (21) by the denominator (8): 21 ÷ 8 = 2.625
This confirms that 2 5/8 is equal to 2.625 in decimal form.
The Significance of Decimal Places
The result, 2.625, has three decimal places. The number of decimal places is determined by the denominator of the original fraction. If the denominator is a power of 10 (like 10, 100, 1000, etc.), the conversion is straightforward. However, when the denominator is not a power of 10, as in this case, the division process may result in a decimal with multiple places, or even a repeating decimal (as is the case with some fractions). In our example, the division results in a terminating decimal—a decimal that ends after a finite number of digits.
Understanding the Division Process
The core of the conversion lies in the division operation. When we divide 5 by 8, we're essentially asking, "How many times does 8 go into 5?" Since 8 is larger than 5, the whole number part of the result is 0. We then add a decimal point and continue the division process by adding zeros after the decimal point in the dividend (5 becomes 5.000). The division continues until either the remainder is zero (resulting in a terminating decimal) or a repeating pattern emerges in the digits (resulting in a repeating decimal).
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is vital in numerous real-world scenarios:
-
Financial Calculations: Dealing with monetary values frequently involves fractions (e.g., calculating interest, discounts, or splitting bills). Converting these fractions to decimals simplifies calculations and provides a clearer understanding of the amounts involved.
-
Measurement and Engineering: Many engineering and scientific calculations require precision. Converting fractional measurements to decimals ensures accurate calculations and precise results.
-
Data Analysis and Statistics: Data analysis often involves calculations using decimal representations of numbers, making conversions necessary for effective data manipulation and interpretation.
-
Computer Programming: Computers primarily work with decimal numbers. Converting fractions to decimals is essential when dealing with numerical data in programming.
-
Everyday Life: Even in everyday activities like cooking (measuring ingredients) or construction (measuring materials), converting fractions to decimals often improves accuracy and clarity.
Frequently Asked Questions (FAQ)
Q1: What if the fraction has a larger numerator than denominator?
A1: If the numerator is larger than the denominator, the fraction is improper. Before converting to a decimal, convert the improper fraction to a mixed number (by dividing the numerator by the denominator and expressing the result as a whole number and a fraction). Then, follow the methods described above. For example, 17/8 would first be converted to 2 1/8.
Q2: What if the fraction results in a repeating decimal?
A2: Some fractions, like 1/3 (which equals 0.3333...), result in repeating decimals. In such cases, you can either round the decimal to a specified number of places or represent the repeating part using a bar notation (e.g., 0.3̅).
Q3: Are there other methods to convert fractions to decimals?
A3: While the division method is the most common and fundamental approach, other techniques exist, especially for fractions with denominators that are easily converted to powers of 10. For instance, 3/5 can be easily converted to 6/10, which is simply 0.6.
Q4: Can I use a calculator to convert fractions to decimals?
A4: Yes, most calculators have the functionality to perform this conversion directly. Simply enter the fraction (numerator divided by denominator) and press the equals button. However, understanding the underlying mathematical process is still essential for building a strong mathematical foundation.
Q5: Why is it important to learn this conversion?
A5: Converting fractions to decimals is a fundamental skill in mathematics that underpins many areas of numerical computation and problem-solving. Mastering this skill will improve your overall mathematical fluency and proficiency in various fields.
Conclusion
Converting fractions to decimals is a crucial skill with broad applications across various disciplines. The conversion of 2 5/8 to 2.625, as demonstrated through the two methods outlined above, highlights the underlying principles and processes involved. Understanding these methods, along with the concepts of mixed numbers, improper fractions, terminating decimals, and repeating decimals, provides a solid foundation for tackling a wide range of mathematical problems involving fractions and decimals. Practice is key to mastering this skill; so keep practicing and you'll become adept at converting fractions to decimals in no time! Remember, a strong understanding of fractions and decimals is a cornerstone of mathematical literacy and a valuable tool in your academic and professional journey.
Latest Posts
Latest Posts
-
Is A Square A Trapezoid
Sep 13, 2025
-
1 2 Oz To Teaspoon
Sep 13, 2025
-
Half A Pound In Oz
Sep 13, 2025
-
Restriction B On Drivers License
Sep 13, 2025
-
18 Degrees Celsius To Fahrenheit
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2 5/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.