2x 1 3 4x 9
cibeltiagestion
Sep 14, 2025 · 6 min read
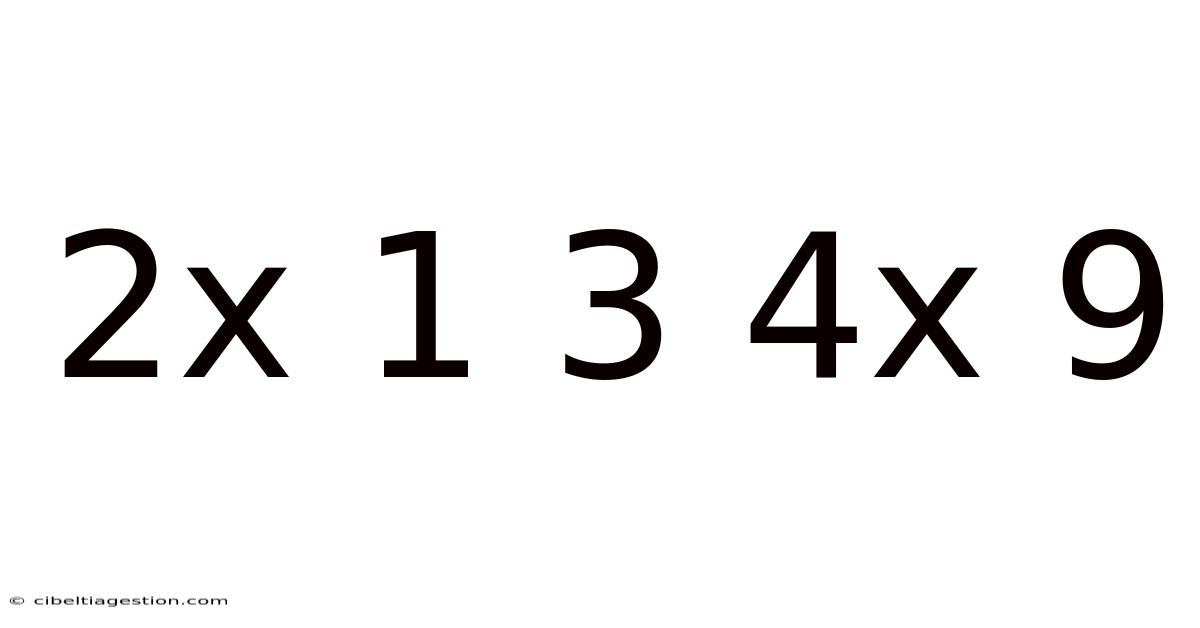
Table of Contents
Decoding the Sequence: Exploring the Mathematical Puzzle of "2x 1 3 4x 9"
This article delves into the intriguing mathematical sequence "2x 1 3 4x 9," exploring its potential interpretations, underlying patterns, and possible solutions. We will examine various mathematical concepts, including arithmetic progressions, geometric progressions, and even consider the possibility of hidden codes or symbolic representations. The goal is not just to find a solution, but to understand the problem-solving process and explore the different avenues of mathematical reasoning. This seemingly simple sequence offers a rich playground for analytical thinking and creative problem-solving.
Understanding the Problem: Defining the Variables
At first glance, "2x 1 3 4x 9" appears ambiguous. The use of "x" creates uncertainty. Does it represent multiplication? An unknown variable? Or perhaps something else entirely? This ambiguity is precisely what makes the sequence so challenging and fascinating. We must consider several possibilities to fully explore the problem.
Let's consider the different interpretations of the "x":
-
Multiplication: The most straightforward interpretation is that "x" represents multiplication. In this case, the sequence becomes: 2 * 1, 3, 4 * 9. This interpretation leaves us with a disjointed sequence of numbers. We need to find a connection or pattern to make sense of it.
-
Unknown Variable: Another possibility is that "x" represents an unknown variable that needs to be solved for. In this case, we are looking for a relationship between the numbers that allows us to determine the value of "x." This interpretation requires a more systematic and analytical approach.
-
Symbolic Representation: Finally, we must consider the possibility that "x" is not a mathematical operator or variable but a symbolic element within a broader code or system. This opens the door to more abstract and creative solutions, requiring us to think outside the typical mathematical framework.
Exploring Arithmetic and Geometric Progressions
Let's investigate whether any standard mathematical sequences can explain the numbers.
Arithmetic Progressions: An arithmetic progression is a sequence where the difference between consecutive terms is constant. For example, 2, 5, 8, 11 is an arithmetic progression with a common difference of 3. The sequence "2x 1 3 4x 9" doesn't immediately fit this pattern. However, we can explore if any manipulation of the sequence or parts of it can lead to an arithmetic progression. We might need to consider removing the "x" or regrouping the numbers.
Geometric Progressions: A geometric progression is a sequence where the ratio between consecutive terms is constant. For example, 2, 6, 18, 54 is a geometric progression with a common ratio of 3. This sequence also doesn’t directly match the given pattern. Again, we might need to consider transformations or alterations to find a geometric progression.
Analyzing the Sequence Using Different Mathematical Operations
We need to explore different mathematical operations to try to reveal a hidden pattern or rule that governs the sequence.
-
Addition and Subtraction: Let’s see if adding or subtracting numbers in the sequence creates a pattern. For example, 3 - 1 = 2, which is the first number. However, this pattern doesn't consistently apply. This approach doesn't seem to reveal any consistent patterns.
-
Multiplication and Division: We can experiment with multiplication and division. We might consider the product or ratio of consecutive numbers or groups of numbers. The multiplication of adjacent numbers does not reveal a pattern.
-
Modulo Operations: This explores the remainders after division. For instance, performing a modulo operation might reveal hidden cyclical patterns. Let's try: 3 mod 2 = 1, and we see a "1" in the sequence. Exploring this more systematically requires various modulo values and potential grouping of the numbers.
-
Prime Factorization: Analyzing the prime factorization of the numbers might reveal patterns. The prime factorization of the numbers 1, 3, and 9 are relatively simple, but it's less obvious for a potential connection with 2 and 4.
The Role of "x" and Potential Solutions
The "x" remains the biggest challenge. If we assume "x" represents multiplication, we still lack a clear, unifying pattern. However, we should consider the possibility of hidden operations. If "x" acts as a separator between two distinct subsequences (2, and 4) and (1, 3, 9), we can look at each subset separately.
One possible (and admittedly speculative) interpretation is that the sequence represents two separate geometric progressions:
- Subset 1 (Even Numbers): 2, 4. This exhibits a common ratio of 2.
- Subset 2 (Odd Numbers): 1, 3, 9. This exhibits a common ratio of 3 (1 x 3 = 3; 3 x 3 = 9).
This doesn't fully unify the entire sequence, but it reveals internal order within subsets. Perhaps there's a higher-level rule connecting these two independent progressions, which might require a more sophisticated mathematical approach.
Beyond Numerical Patterns: Symbolic Interpretation
Let's entertain the possibility that "2x 1 3 4x 9" has a symbolic representation.
-
Base-Conversion: Consider the possibility that the numbers are represented in a different base than base-10. A conversion might unveil a clear pattern not easily visible in base-10.
-
Coded Message: The sequence might be a coded message where the numbers represent letters in an alphabet or elements in a code. However, without additional information or context, this is purely speculative.
-
Geometric Representation: Perhaps the sequence represents points on a geometric plane, and the "x" symbolizes a spatial relationship between these points. This could lead to a geometrical solution.
Frequently Asked Questions (FAQ)
-
Q: Is there a single definitive answer? A: No. Without more context or a clear definition of "x," multiple interpretations and solutions are possible. The challenge lies in exploring the possibilities and applying different mathematical concepts to find potential patterns.
-
Q: Why is this sequence so difficult? A: The ambiguity of "x" and the lack of an immediately obvious pattern make it a challenging puzzle. It encourages exploration of multiple mathematical concepts and analytical approaches.
-
Q: What mathematical skills are needed to solve this type of problem? A: Problem-solving skills, familiarity with arithmetic and geometric progressions, understanding of different mathematical operations (including modulo operations), and the ability to think creatively and consider multiple interpretations are all necessary skills.
Conclusion: The Importance of Exploration
The sequence "2x 1 3 4x 9" serves as a compelling example of how a seemingly simple problem can open up a wealth of mathematical exploration. The lack of a single definitive answer emphasizes the importance of considering multiple interpretations, applying various mathematical techniques, and employing creative problem-solving strategies. It highlights the dynamic nature of mathematics and the need for both analytical rigor and flexible thinking. The process of exploring different approaches, even if they don't lead to a universally accepted solution, is valuable in developing critical thinking and mathematical intuition. The true success isn't necessarily finding the answer, but in the journey of discovery and the expansion of mathematical understanding. It encourages further exploration and the application of more advanced mathematical concepts for those interested in pursuing deeper investigations.
Latest Posts
Latest Posts
-
Big Ideas Integrated Math 1
Sep 14, 2025
-
Unproctored Placement Assessment Answer Key
Sep 14, 2025
-
Scientific Name For A Sheep
Sep 14, 2025
-
Which Term Describes An Enzyme
Sep 14, 2025
-
Formula For Mercury Ii Oxide
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2x 1 3 4x 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.