2y 3 5 1 2
cibeltiagestion
Sep 16, 2025 · 6 min read
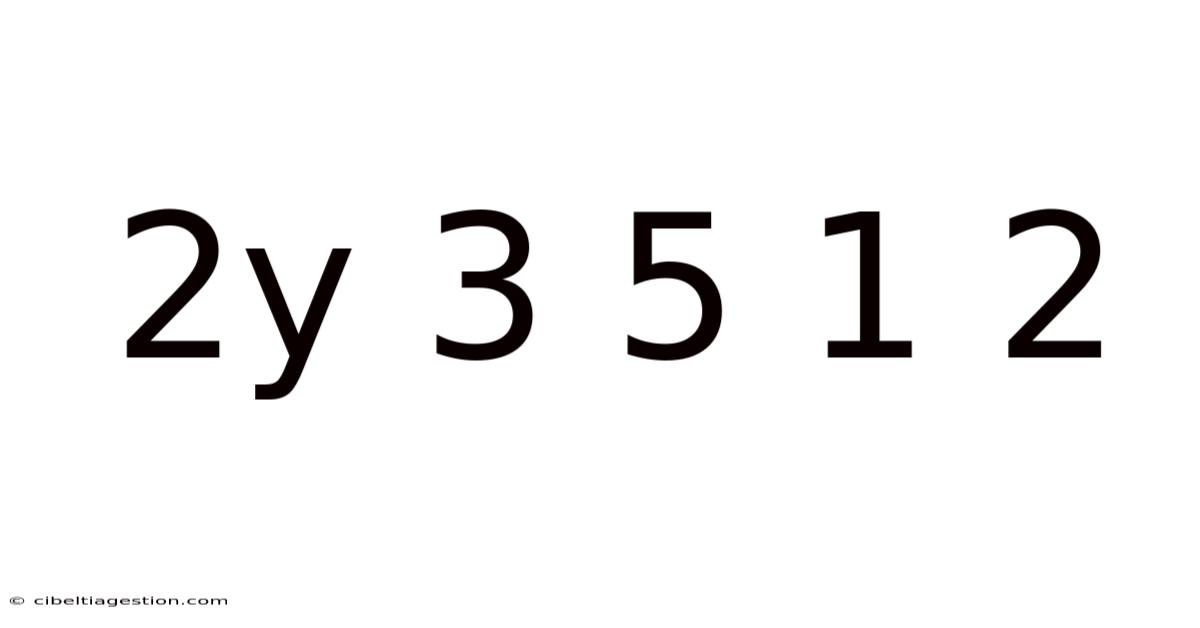
Table of Contents
Decoding the Sequence: Exploring the Mathematical and Logical Possibilities of "2y 3 5 1 2"
This article delves into the intriguing sequence "2y 3 5 1 2," exploring its potential interpretations from a mathematical and logical perspective. The presence of the variable 'y' introduces an element of uncertainty, prompting us to consider various possibilities and the methods used to solve such sequences. We'll examine different approaches, including pattern recognition, algebraic manipulation, and the application of number theory concepts. This investigation aims to not only decipher the sequence but also to illustrate problem-solving strategies applicable to similar mathematical puzzles.
Understanding the Problem: Defining the Scope
The sequence "2y 3 5 1 2" presents a unique challenge. The inclusion of the variable 'y' signifies that the sequence might represent a more complex mathematical relationship rather than a simple arithmetic or geometric progression. We need to consider several scenarios:
- 'y' as a fixed unknown: This assumes 'y' represents a specific, albeit currently unknown, numerical value. Our task becomes finding the value of 'y' that makes the sequence follow a discernible pattern.
- 'y' as a variable: This implies the sequence could represent a function or formula where 'y' is the input and the subsequent numbers are the output based on a particular rule.
- 'y' as a placeholder: It's possible 'y' represents a missing element in an otherwise recognizable pattern. This approach necessitates exploring various substitutions for 'y' to discover a consistent pattern.
Approaches to Solving the Sequence: A Multifaceted Analysis
Let's explore different approaches to analyze and potentially solve the sequence:
1. Pattern Recognition: Searching for Underlying Relationships
The most intuitive approach is to look for patterns within the known elements of the sequence (3, 5, 1, 2). We can investigate:
- Arithmetic Differences: Calculating the differences between consecutive numbers doesn't reveal a consistent pattern. (5-3=2, 1-5=-4, 2-1=1)
- Geometric Ratios: Similarly, dividing consecutive numbers doesn't produce a consistent ratio.
- Modulo Operations: Exploring modulo arithmetic (remainders after division) might reveal hidden patterns. However, without a clear hypothesis, this method proves inefficient for this specific sequence.
- Fibonacci-like Sequences: Although the numbers don't directly follow the Fibonacci sequence (each number is the sum of the two preceding ones), variations or modifications of this sequence could potentially fit the given data. This requires further investigation and potentially adjusting the sequence to accommodate the 'y' variable.
2. Algebraic Manipulation: Exploring Equations and Functions
Given the presence of 'y', an algebraic approach is necessary. We can attempt to formulate an equation or function that generates the sequence. This could involve:
- Linear Equations: Attempting to fit a linear equation of the form
a*n + b, where 'n' represents the position of the element in the sequence and 'a' and 'b' are constants. However, with four known values and five elements, a simple linear equation is unlikely to be successful. - Polynomial Functions: More complex polynomial functions could potentially fit the sequence. This would involve solving a system of equations, which may lead to multiple solutions depending on the degree of the polynomial.
- Recursive Relations: We could explore recursive relationships where each element depends on the preceding one or several preceding elements. For example, we might hypothesize a relationship like
a_n = f(a_(n-1), a_(n-2), ...)wherea_nis the nth element and 'f' is a function to be determined. This approach is highly dependent on our intuition and the chosen function.
3. Number Theory Concepts: Exploring Advanced Mathematical Tools
More advanced number theory concepts could be employed, albeit without a clear indication of applicability based on the limited information available. These concepts include:
- Modular Arithmetic: As mentioned earlier, this method could be helpful in revealing underlying patterns, but its effectiveness requires a more defined hypothesis.
- Prime Number Distribution: Examining the prime factorization of the numbers in the sequence might reveal subtle connections. However, with only a few numbers, this is unlikely to provide a decisive solution.
- Diophantine Equations: If we assume 'y' and other elements are integers, this area of number theory deals with solving equations in integers. However, forming appropriate equations requires further assumptions and observations.
Case Studies: Exploring Specific Scenarios
To illustrate different approaches, let's consider specific scenarios:
Scenario 1: 'y' as a specific value
Let's assume 'y' is an integer. If we postulate a simple arithmetic pattern, it's unlikely to fit the given data (3, 5, 1, 2). However, if we consider a more complex relationship (e.g., a polynomial function), several possible solutions might exist. Finding the "best" solution requires further criteria, such as simplicity and elegance.
Scenario 2: 'y' as a variable in a recursive function
We could explore recursive functions. For instance, consider a function where each element is a modular operation on the previous one: a_n = (a_(n-1) * x + c) mod m. Finding the suitable values for x, c, and m that generate the sequence, and subsequently including 'y', would involve extensive trial and error.
Scenario 3: 'y' as a placeholder in a larger sequence
The sequence could be a fragment of a larger, repeating sequence. In this case, 'y' would be the missing element that completes a repeating pattern. This necessitates exploring different values for 'y' and looking for a repeating sequence that would make sense mathematically.
Addressing Potential Solutions and Their Limitations
The lack of context makes definitively solving the sequence challenging. Any proposed solution will inherently involve assumptions and might not be unique. For instance, we could create a polynomial function that fits the given numbers including a specific value for 'y'. However, this function might not accurately predict future elements. Similarly, a recursive function fitting the given data could have limited predictive power or lack a theoretical foundation.
Therefore, a crucial step is formulating a hypothesis based on pattern recognition, then testing it against available data and potential extensions of the sequence. This iterative process of hypothesis formulation, testing, and refinement is essential.
Frequently Asked Questions (FAQ)
-
Q: Is there a single correct answer to this sequence? A: Without additional context or constraints, there's no guarantee of a single correct answer. Several mathematical relationships could potentially generate the sequence, each with its own limitations and assumptions.
-
Q: What if 'y' is not a number but a symbol? A: If 'y' represents a symbol with a specific mathematical meaning (e.g., a function or operator), the sequence's interpretation would significantly change. Further clarification is necessary to approach this scenario.
-
Q: How can I improve my problem-solving skills for similar sequences? A: Practice with various mathematical puzzles and sequences. Familiarize yourself with different mathematical concepts and tools. The ability to identify patterns, formulate hypotheses, and rigorously test them is crucial. Also, exploring different approaches like recursion and polynomial functions helps broaden your problem-solving capabilities.
Conclusion: The Ongoing Search for Understanding
The sequence "2y 3 5 1 2" serves as an excellent example of a mathematical puzzle requiring critical thinking and a multi-faceted approach. While a definitive solution remains elusive without additional information, the exploration process has highlighted several important problem-solving strategies. The iterative process of hypothesis testing, combined with a solid understanding of mathematical concepts, is key to tackling such problems. The presence of the 'y' variable underscores the importance of flexibility and considering various possibilities when interpreting mathematical sequences and patterns. Further investigation and the addition of constraints or context could potentially lead to a more precise and well-defined solution.
Latest Posts
Latest Posts
-
What Is 25 Of 24
Sep 16, 2025
-
The Phrase Transacting Business Includes
Sep 16, 2025
-
Waxing Moon Vs Waning Moon
Sep 16, 2025
-
30 Years How Many Days
Sep 16, 2025
-
Centrifugal Force Ap Human Geography
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2y 3 5 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.