3.26d + 9.75d - 2.65
cibeltiagestion
Sep 06, 2025 · 5 min read
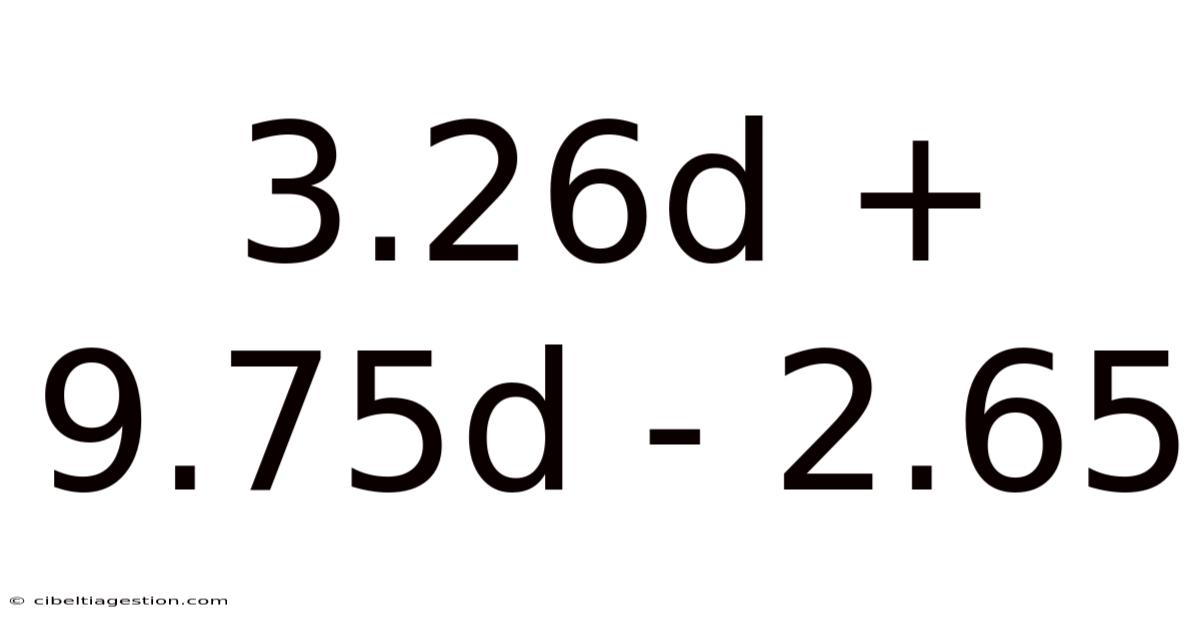
Table of Contents
Demystifying 3.26d + 9.75d - 2.65: A Deep Dive into Algebraic Expressions
This article provides a comprehensive explanation of the algebraic expression 3.26d + 9.75d - 2.65, covering its simplification, application in various contexts, and answering frequently asked questions. Understanding this type of expression is crucial for anyone studying algebra, as it forms the basis for more complex equations and problem-solving. We will delve into the intricacies of combining like terms, the importance of order of operations (PEMDAS/BODMAS), and the practical implications of working with decimal coefficients.
Understanding the Components
Before we delve into the solution, let's break down the expression: 3.26d + 9.75d - 2.65. This is an algebraic expression because it contains variables (letters representing unknown values) and constants (numerical values).
- d: This is the variable. It represents an unknown quantity. We can think of 'd' as a placeholder for any number.
- 3.26, 9.75, and -2.65: These are the coefficients. They are the numerical factors that multiply the variable (in the case of 3.26d and 9.75d) or are constant terms. Notice that -2.65 is a negative constant. This is important for correct calculations.
- +, and -: These are the operators, indicating addition and subtraction.
Simplifying the Expression
The key to simplifying this expression lies in combining like terms. Like terms are terms that have the same variable raised to the same power. In our expression, 3.26d and 9.75d are like terms because both have the variable 'd' raised to the power of 1 (although the '1' isn't explicitly written, it's implied). The constant term, -2.65, is not a like term with the 'd' terms.
To simplify:
-
Combine the 'd' terms: Add the coefficients of the like terms: 3.26 + 9.75 = 13.01. This gives us 13.01d.
-
Retain the constant term: The constant term, -2.65, remains unchanged.
Therefore, the simplified expression is 13.01d - 2.65. This is the most concise and mathematically correct way to represent the original expression.
Applying the Simplified Expression
The usefulness of simplifying this expression becomes evident when we want to evaluate it for a specific value of 'd'. Let's consider some examples:
Example 1: d = 2
Substitute d = 2 into the simplified expression:
13.01(2) - 2.65 = 26.02 - 2.65 = 23.37
Therefore, when d = 2, the expression 3.26d + 9.75d - 2.65 equals 23.37.
Example 2: d = -5
Substitute d = -5 into the simplified expression:
13.01(-5) - 2.65 = -65.05 - 2.65 = -67.70
Therefore, when d = -5, the expression 3.26d + 9.75d - 2.65 equals -67.70
Example 3: Real-World Application
Imagine you're calculating the total cost of a project. Let's say 'd' represents the number of days worked. 3.26d could represent the cost of labor for one type of work, 9.75d the cost of labor for another type, and -2.65 represents a discount or rebate. The simplified expression, 13.01d - 2.65, gives you a streamlined formula to calculate the total cost based on the number of days worked.
The Importance of Order of Operations (PEMDAS/BODMAS)
While this particular expression doesn't involve parentheses or exponents, understanding the order of operations (PEMDAS/BODMAS) is crucial when dealing with more complex algebraic expressions. PEMDAS/BODMAS stands for:
- Parentheses (Brackets)
- Exponents (Orders)
- Multiplication and Division (from left to right)
- Addition and Subtraction (from left to right)
Always follow this order to ensure you arrive at the correct result.
Working with Decimal Coefficients
This example highlights the importance of accurately handling decimal numbers in algebraic expressions. When combining like terms with decimal coefficients, ensure you perform the addition and subtraction correctly, paying close attention to the decimal points and signs. Calculators can be helpful tools, but understanding the underlying mathematical principles is essential to avoid errors and to interpret the results meaningfully.
Expanding the Concept: More Complex Expressions
The principles discussed here can be applied to more complex algebraic expressions. For instance, consider the expression: 2.5(3d + 4) + 7.2d - 1.8. This would involve using the distributive property (multiplying the 2.5 by each term inside the parenthesis) before combining like terms. Following the order of operations will be crucial in such scenarios.
Frequently Asked Questions (FAQ)
Q1: What if the expression involved different variables, for example, 3.26d + 9.75e - 2.65?
A1: In this case, you cannot combine 3.26d and 9.75e because they are unlike terms (different variables). The simplified expression would remain as 3.26d + 9.75e - 2.65.
Q2: Can I solve for 'd' in the expression 13.01d - 2.65 = 0?
A2: Yes, this is a simple linear equation. To solve for 'd', add 2.65 to both sides, resulting in 13.01d = 2.65. Then, divide both sides by 13.01: d = 2.65 / 13.01 ≈ 0.2037.
Q3: What are some real-world applications of this type of algebraic expression beyond the cost calculation example?
A3: Many real-world scenarios use similar expressions. This includes calculations involving:
- Physics: Formulas related to motion, force, and energy often involve variables and constants.
- Engineering: Designing structures and systems frequently requires algebraic calculations.
- Finance: Calculating interest, profits, and losses often utilizes algebraic expressions.
- Chemistry: Stoichiometry problems in chemistry rely heavily on algebraic equations.
Conclusion
The algebraic expression 3.26d + 9.75d - 2.65, while seemingly simple, provides a foundational understanding of key algebraic concepts like combining like terms, simplifying expressions, and working with decimal coefficients. Mastering these concepts is crucial for success in higher-level mathematics and various fields where mathematical modeling and problem-solving are essential. Remember the importance of the order of operations and the ability to apply these principles to more complex scenarios to build a strong foundation in algebra. The ability to simplify and evaluate such expressions is a fundamental skill in numerous academic and professional disciplines. By understanding the underlying principles, you can confidently tackle more complex algebraic challenges.
Latest Posts
Latest Posts
-
Convert 37 7 Celsius To Fahrenheit
Sep 06, 2025
-
Proving The Parallelogram Side Theorem
Sep 06, 2025
-
Similarities Between Romanticism And Transcendentalism
Sep 06, 2025
-
4 Foot 5 In Inches
Sep 06, 2025
-
Exit 25 Mph Sign Meaning
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 3.26d + 9.75d - 2.65 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.