3 4 3 4 Equals
cibeltiagestion
Sep 17, 2025 · 5 min read
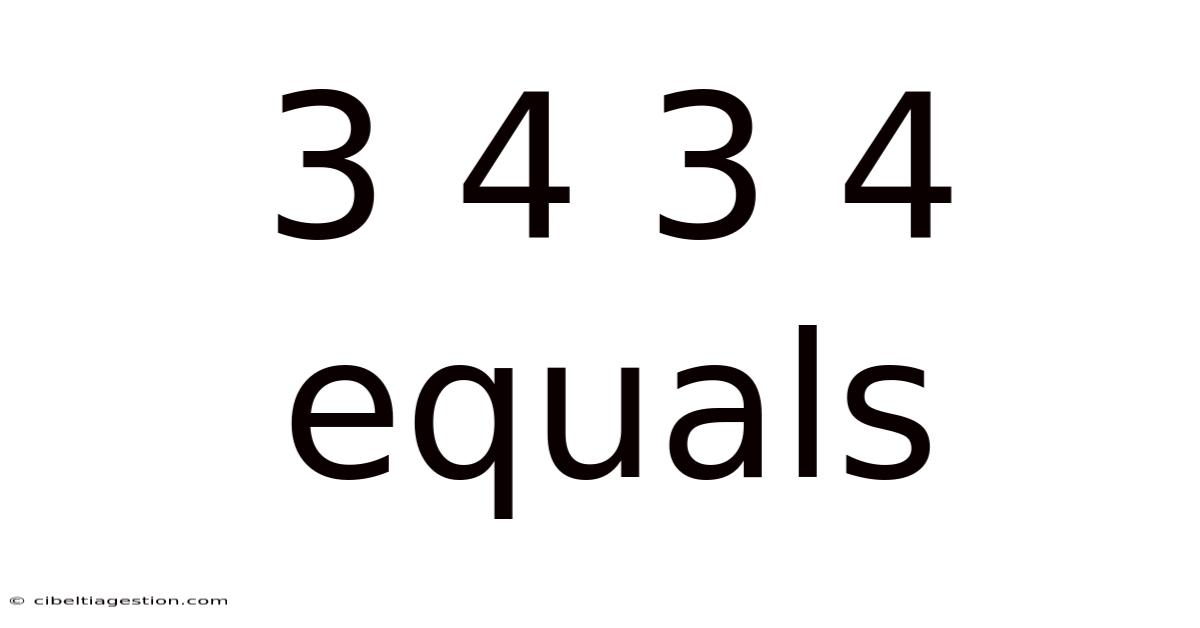
Table of Contents
Decoding the Enigma: 3 4 3 4 Equals... What?
The seemingly simple equation "3 4 3 4 equals..." is far more complex than it initially appears. It's not a straightforward mathematical problem with a single, definitive answer. Instead, it's a puzzle that tests our understanding of mathematical operations, logical reasoning, and the importance of context. This article will explore various potential interpretations, delve into the mathematical principles involved, and demonstrate how seemingly simple sequences can harbor surprising depths. We'll examine the possibilities, from basic arithmetic to more advanced mathematical concepts, and even touch upon the potential for creative interpretations. Understanding the different approaches will highlight the importance of clear communication and the limitations of ambiguous notation.
Understanding the Ambiguity: Why There's No Single Answer
The core issue with "3 4 3 4 equals..." lies in the lack of an explicit operator between the numbers. In standard mathematical notation, we use symbols like +, -, ×, and ÷ to indicate addition, subtraction, multiplication, and division, respectively. The absence of these symbols leaves the equation open to interpretation. We could interpret the sequence as representing various mathematical operations or even a completely different system altogether.
Possible Interpretations and Solutions
Let's explore some of the possible interpretations and the resulting solutions:
1. Concatenation:
The simplest interpretation is to treat the sequence as a concatenation of numbers. This means simply combining the digits to form a larger number. Therefore:
3 4 3 4 = 3434
This is a perfectly valid interpretation, particularly if the context suggests a numerical identification system or a code.
2. Arithmetic Operations: Exploring Multiple Combinations
A more complex approach involves exploring different combinations of arithmetic operations. Because we lack specified operators, we can freely insert them:
- Addition: 3 + 4 + 3 + 4 = 14
- Subtraction: 3 - 4 - 3 - 4 = -8 (or various other combinations depending on the order)
- Multiplication: 3 × 4 × 3 × 4 = 144
- Division: This becomes tricky without parentheses to specify the order of operations. For instance, (3 × 4) / (3 × 4) = 1, but 3 / 4 × 3 × 4 = 9. Different groupings lead to vastly different results.
- Mixed Operations: We could explore combinations of addition, subtraction, multiplication, and division. The number of possibilities expands exponentially, leading to a multitude of solutions. For example: (3 + 4) × (3 - 4) = -7; (3 × 4) + 3 - 4 = 11; 3 + 4 × 3 + 4 = 19; etc.
The lack of defined operators makes this approach inherently ambiguous. A solution arrived at using this method would only be correct within the specific context of the chosen operations.
3. Base Systems:
Could the numbers represent different base systems? While unlikely without further information, this is a possibility. In base 10 (our standard decimal system), the numbers are already represented. However, if we assume a different base, the values would change. For example:
- Base 2 (Binary): 3 and 4 aren't directly representable in binary without conversion.
- Base 16 (Hexadecimal): 3 and 4 are easily represented, but the interpretation remains ambiguous regarding the operators.
4. Mathematical Functions:
Going beyond basic arithmetic, we could introduce mathematical functions. However, without any indication of which function is intended, this becomes entirely speculative.
5. Sequences and Patterns:
A more abstract interpretation could involve recognizing sequences or patterns. For example, one might identify a repeating pattern: 3, 4, 3, 4,... This doesn't inherently provide a numerical answer, but it reveals a structural property of the sequence.
6. Creative Interpretations:
Stepping outside the purely mathematical realm, one might consider creative interpretations. For instance, the sequence could be seen as a musical rhythm, a simple code in cryptography, or a pattern in visual art.
The Importance of Context and Notation
The ambiguity of "3 4 3 4 equals..." underscores the critical role of context and precise mathematical notation. Ambiguous expressions are prone to misinterpretation and can lead to wildly different results depending on the assumptions made. In any mathematical context, clear communication is paramount. The use of parentheses to establish the order of operations and explicit symbols for operators are crucial in preventing ambiguity and ensuring a single, unambiguous solution.
Mathematical Principles in Play
This seemingly simple puzzle touches on several key mathematical principles:
- Order of Operations (PEMDAS/BODMAS): The standard order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) guides the evaluation of expressions with multiple operators. The absence of operators in our puzzle renders this principle inapplicable directly.
- Number Systems: The puzzle subtly reminds us that numbers can be represented in various systems (base 10, base 2, base 16, etc.), altering their values and interpretations.
- Ambiguity and Precision: The exercise highlights the importance of precise notation and avoiding ambiguity in mathematical expressions. Without clear symbols and parentheses, the interpretation is subjective.
- Combinatorics and Permutations: When exploring various combinations of arithmetic operations, we encounter concepts of combinatorics, dealing with the number of ways to arrange or select items from a set.
Frequently Asked Questions (FAQ)
Q: What is the one correct answer to 3 4 3 4 equals...?
A: There isn't one single correct answer. The absence of operators makes the expression inherently ambiguous. Different interpretations lead to different results.
Q: Is there a hidden trick or pattern I'm missing?
A: The main "trick" is the inherent ambiguity of the notation. There is no hidden mathematical trick; the challenge lies in understanding the lack of precision and exploring the possibilities.
Q: How can I solve this kind of problem in the future?
A: Look for clearly defined operators and parentheses. If these are absent, consider the context of the problem. If there is no specific context, then acknowledge that multiple answers are possible, each based on different assumptions.
Conclusion: Beyond the Numbers
The puzzle of "3 4 3 4 equals..." serves as a valuable reminder of the importance of clear communication and the power of ambiguity in mathematics. While there’s no single “correct” answer, exploring the various possibilities expands our understanding of numerical systems, mathematical operations, and the limitations of imprecise notation. The puzzle transcends simple arithmetic, prompting reflection on the principles of logic, pattern recognition, and the need for precise mathematical language. It's a small puzzle with surprisingly profound implications for how we approach mathematical problems and communicate mathematical ideas. The journey to unravel its possibilities is as educational as any definitive answer could ever be.
Latest Posts
Latest Posts
-
What Is 120 Of 20
Sep 17, 2025
-
Evaluate Log1255 Mc001 1 Jpg Mc001 2 Jpg Mc001 3 Jpg
Sep 17, 2025
-
Advantages And Disadvantages Of Hcs
Sep 17, 2025
-
2 Lbs To Cups Conversion
Sep 17, 2025
-
1 7 8 In Decimal
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 4 3 4 Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.