3.5 Percent As A Decimal
cibeltiagestion
Sep 06, 2025 · 5 min read
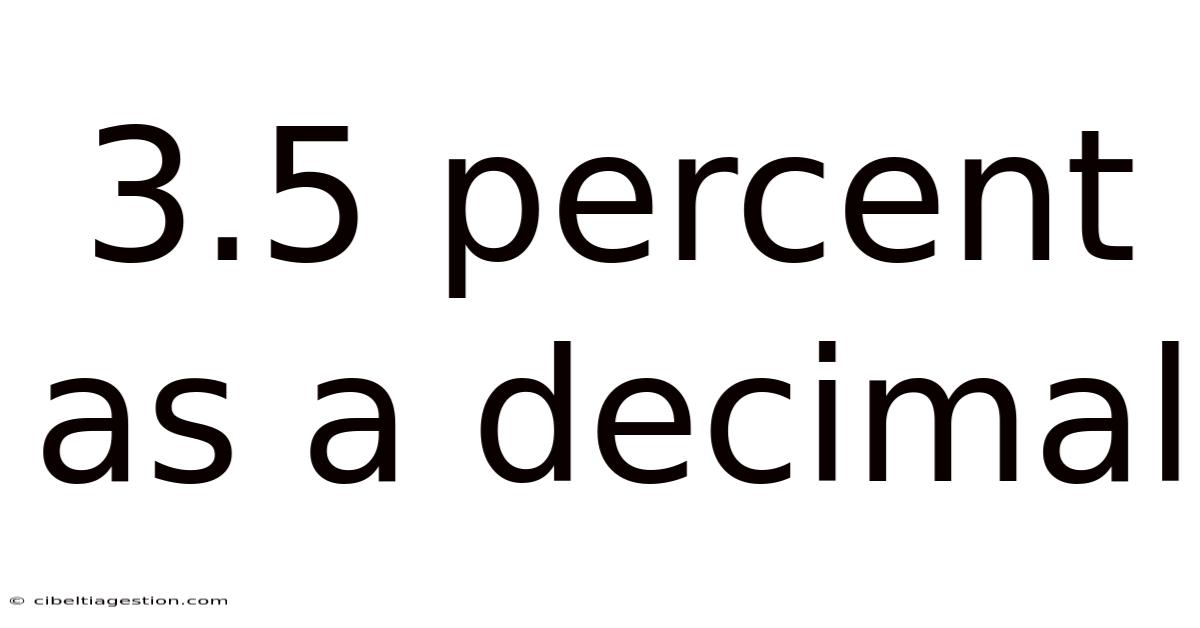
Table of Contents
3.5 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and crucial for various applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This comprehensive guide delves into the conversion of percentages to decimals, focusing specifically on how to represent 3.5 percent as a decimal, and expands on the broader concepts involved. We will explore the underlying principles, provide step-by-step instructions, and address common questions and misconceptions. This will equip you with a solid understanding not just of this specific conversion, but also the broader concept of percentage-decimal interconversion.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "per hundred". Therefore, 3.5 percent means 3.5 parts out of 100. We can represent this mathematically as a fraction: 3.5/100. Percentages are used to represent proportions, rates, and changes in various contexts. For instance, a 10% discount means you save 10 out of every 100 units of currency. A 5% increase in sales signifies a rise of 5 units for every 100 units sold previously.
Converting Percentages to Decimals: The Core Concept
The conversion from a percentage to a decimal involves a straightforward process. Since a percentage is essentially a fraction with a denominator of 100, the conversion simply involves dividing the percentage by 100. Alternatively, a quicker method is to move the decimal point two places to the left.
Method 1: Dividing by 100
To convert 3.5% to a decimal, we divide 3.5 by 100:
3.5 ÷ 100 = 0.035
Method 2: Moving the Decimal Point
This is a quicker and more efficient method, especially for mental calculations. The decimal point in 3.5% is implicitly located after the 5 (3.5%). Moving this decimal point two places to the left gives us 0.035.
Therefore, 3.5% as a decimal is 0.035.
Step-by-Step Guide: Converting Any Percentage to Decimal
The methods outlined above can be applied to any percentage. Here's a general step-by-step guide:
- Identify the percentage: Determine the percentage value you wish to convert.
- Remove the percent sign (%): Discard the percentage symbol.
- Divide by 100 (or move the decimal point two places to the left): This is the core conversion step. Choose whichever method suits your preference and computational comfort.
- The result is the decimal equivalent: The resulting value is the decimal representation of your original percentage.
Examples:
- 15%: 15 ÷ 100 = 0.15 (or move the decimal point in 15. to become 0.15)
- 2.75%: 2.75 ÷ 100 = 0.0275 (or move the decimal point in 2.75 to become 0.0275)
- 125%: 125 ÷ 100 = 1.25 (or move the decimal point in 125. to become 1.25)
Understanding the Significance of Decimal Representation
The decimal form of a percentage offers several advantages. It's easier to use in many mathematical operations, particularly when dealing with calculations involving other decimals or fractions. For example, if you need to calculate 3.5% of a certain amount (say, $500), using the decimal equivalent (0.035) simplifies the calculation considerably: 0.035 x $500 = $17.50. Using the percentage directly would require an extra step of dividing by 100.
Furthermore, decimal representation is crucial for using percentages in computer programs and spreadsheets, as computers fundamentally operate using numerical values.
Practical Applications of Percentage-Decimal Conversion
The ability to seamlessly convert between percentages and decimals is paramount across diverse fields:
- Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns.
- Statistics: Representing proportions, probabilities, and data analysis.
- Science: Expressing experimental results, error margins, and concentration levels.
- Business: Analyzing sales figures, market shares, and growth rates.
- Everyday Life: Understanding sales discounts, calculating tips, and interpreting various statistics.
Frequently Asked Questions (FAQs)
Q1: Why do we divide by 100 or move the decimal point two places to the left when converting percentages to decimals?
A1: Because a percentage represents a fraction out of 100. Dividing by 100 or moving the decimal point two places to the left is simply a mathematical shorthand for this division.
Q2: Can I convert decimals back to percentages?
A2: Absolutely! To convert a decimal back to a percentage, simply multiply by 100 and add the percent sign (%). For example, 0.035 x 100 = 3.5%, 0.15 x 100 = 15%.
Q3: What about percentages greater than 100%?
A3: Percentages greater than 100% are perfectly valid and represent values exceeding the whole amount. For example, 125% represents 125 out of 100, or 1.25 times the original amount. Conversion to decimal follows the same rules: 125% = 1.25.
Q4: How do I handle percentages with fractions?
A4: Convert the fraction to a decimal first, then add it to the whole number before converting the resulting number to a percentage. For example, 5 1/2% would be converted as follows:
- Convert the fraction 1/2 to a decimal: 1 ÷ 2 = 0.5
- Add the whole number: 5 + 0.5 = 5.5
- Convert to a decimal by dividing by 100: 5.5 ÷ 100 = 0.055
Q5: Are there any online calculators to help with these conversions?
A5: Yes, many online calculators are available to aid in percentage-to-decimal and decimal-to-percentage conversions. However, mastering the manual conversion method is highly recommended for improved mathematical understanding and proficiency.
Conclusion
Converting 3.5 percent to its decimal equivalent, 0.035, is a fundamental skill with far-reaching applications. Understanding this conversion is not just about a single numerical manipulation but signifies grasping the core relationship between percentages and decimals. The simple process of dividing by 100 or moving the decimal point two places to the left unlocks a broader understanding of proportional representation, essential for navigating various quantitative scenarios in academic, professional, and everyday contexts. Mastering this skill provides a crucial foundation for more complex mathematical computations and a deeper understanding of the numerical world around us. Practice makes perfect – the more you work with these conversions, the more intuitive and effortless they will become.
Latest Posts
Latest Posts
-
8 5 X 5 5
Sep 06, 2025
-
15 409 In Expanded Form
Sep 06, 2025
-
Which Sentence Contains A Participle
Sep 06, 2025
-
Lewis Dot Structure For Ch3coch3
Sep 06, 2025
-
By Stimulating Secretion Of Peptidases
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 3.5 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.