3 Times What Equals 2
cibeltiagestion
Sep 09, 2025 · 5 min read
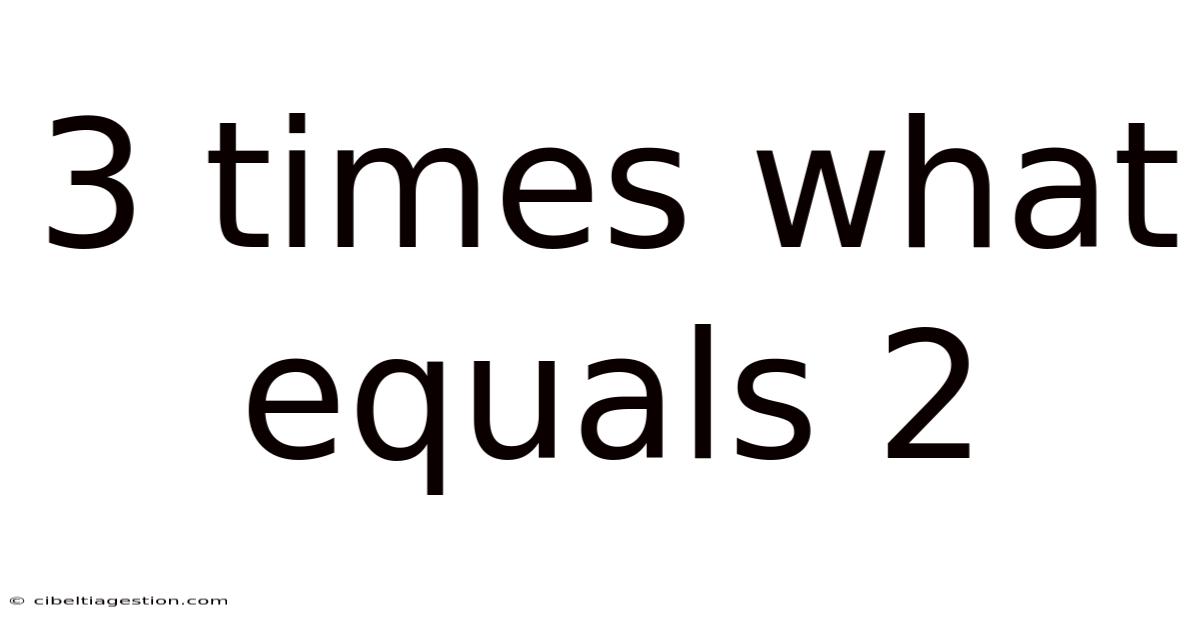
Table of Contents
Unveiling the Mystery: 3 Times What Equals 2? A Deep Dive into Mathematical Concepts
Finding the answer to "3 times what equals 2" might seem straightforward at first glance, but it opens a door to exploring fundamental mathematical concepts, including fractions, decimals, and the power of algebraic reasoning. This article will not only provide the solution but delve deeper into the underlying principles, offering a comprehensive understanding for learners of all levels. We'll explore various approaches to solving this seemingly simple equation and connect it to broader mathematical applications.
Understanding the Problem: A Simple Equation
The problem "3 times what equals 2" can be expressed as a simple algebraic equation: 3x = 2. Here, 'x' represents the unknown value we need to find. The equation states that three times this unknown value ('x') results in 2. This is a fundamental type of equation, a linear equation in one variable, that forms the bedrock of algebra.
Solving the Equation: Step-by-Step Approach
To solve for 'x', we need to isolate it on one side of the equation. We achieve this by performing the inverse operation of multiplication, which is division.
Step 1: Divide both sides of the equation by 3.
This gives us: 3x / 3 = 2 / 3
Step 2: Simplify the equation.
The left side simplifies to 'x', leaving us with: x = 2/3
Therefore, the answer is 2/3. Three times two-thirds (3 * (2/3)) equals 2.
Representing the Solution: Fractions and Decimals
The solution, 2/3, is a fraction. Fractions represent parts of a whole. In this case, 2/3 represents two parts out of a total of three equal parts.
We can also represent 2/3 as a decimal. To convert a fraction to a decimal, we divide the numerator (the top number) by the denominator (the bottom number):
2 ÷ 3 ≈ 0.666666...
The decimal representation of 2/3 is a repeating decimal, meaning the digit 6 repeats infinitely. We often round repeating decimals for practical purposes, for example, to 0.67. However, it's important to remember that the precise value remains 2/3.
Visualizing the Solution: Geometric Representation
Visualizing mathematical concepts can significantly enhance understanding. Let's consider a geometric approach to understand 2/3.
Imagine a rectangle divided into three equal parts. Shading two of these parts represents the fraction 2/3. If the total area of the rectangle represents the number 2, then each of the three equal parts has an area of 2/3. This visual representation reinforces the concept of the fraction as a part of a whole.
Extending the Concept: Proportions and Ratios
The problem "3 times what equals 2" can also be approached using the concept of proportions and ratios. A proportion is a statement that two ratios are equal. We can set up a proportion as follows:
3/x = 2/y
Where 'x' is the unknown value we are solving for and 'y' is a chosen value representing a corresponding part of the whole. For simplicity, let's set y = 1. Then the proportion becomes:
3/x = 2/1
Cross-multiplying, we get:
3 * 1 = 2 * x
3 = 2x
Dividing both sides by 2, we again arrive at:
x = 3/2 = 1.5
This approach illustrates a slightly different perspective, showing how the unknown value relates proportionally to other values. While this example gives 1.5 it's crucial to understand the context. We chose to solve for an equivalent ratio, which differs from the question's direct solution, providing further insight into the interrelation of mathematical concepts.
Applying the Concept: Real-World Examples
Understanding fractions and solving equations like 3x = 2 has numerous real-world applications. Here are a few examples:
-
Baking: A recipe calls for 2 cups of flour, but you only want to make 2/3 of the recipe. You would calculate (2/3) * 2 cups = 4/3 cups of flour, showcasing the application of fraction multiplication in practical scenarios.
-
Construction: Dividing materials for a project. If a construction project requires 2 meters of wood, and you need to divide that across three parts of a project evenly, this means you would use approximately 0.67 meters per part.
-
Finance: Calculating portions of a budget. If you have a budget of $2, and you want to spread that among three things evenly, each thing receives roughly $0.67.
Beyond the Basics: More Complex Equations
While 3x = 2 is a simple linear equation, understanding its solution forms a foundation for tackling more complex equations. The same principles of isolating the variable through inverse operations apply to more intricate algebraic problems. For example, consider the following problem:
5x + 7 = 12
To solve this equation, we use the same principles of inverse operations:
- Subtract 7 from both sides: 5x = 5
- Divide both sides by 5: x = 1
This shows that the same fundamental process of manipulating equations is applicable, regardless of added complexity.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this equation?
A: Yes, absolutely! Calculators are helpful for performing the division 2 ÷ 3 to obtain the decimal representation of the solution. However, it's crucial to understand the underlying mathematical principles involved.
Q: What if the equation was 3x = -2?
A: The process is the same. Divide both sides by 3, resulting in x = -2/3 or approximately x = -0.67. The negative sign simply indicates a negative value for 'x'.
Q: Is there only one solution to this equation?
A: Yes, for a linear equation like 3x = 2, there is only one solution. This is because it's a one-to-one function; each input value has only one unique output.
Conclusion: Mastering Mathematical Fundamentals
The seemingly simple equation 3x = 2 provides a gateway to a deeper understanding of fundamental mathematical concepts. By understanding how to solve this equation, you gain proficiency in algebraic manipulation, fraction representation, decimal conversion, and proportion calculation. These are essential skills that extend far beyond simple arithmetic, forming the basis for more advanced mathematical studies and countless practical applications in everyday life. Mastering this basic concept unlocks a broader appreciation for the elegance and power of mathematics.
Latest Posts
Latest Posts
-
5 1 4 Access For Dna Class
Sep 09, 2025
-
Is Proline Polar Or Nonpolar
Sep 09, 2025
-
Comprehensive Problem 2 Part 5
Sep 09, 2025
-
Standoff Mounting Allows For Better
Sep 09, 2025
-
First Hundred Digits Of Pi
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 3 Times What Equals 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.