32.5 Percent As A Decimal
cibeltiagestion
Sep 14, 2025 · 5 min read
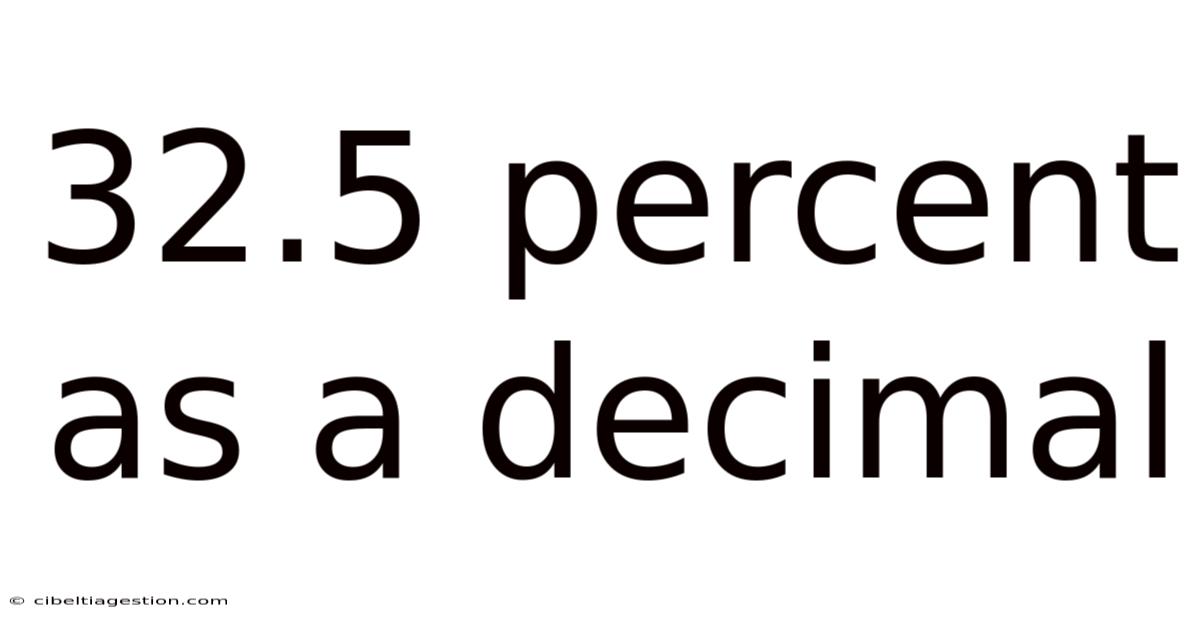
Table of Contents
32.5 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and across numerous fields, from finance and statistics to everyday calculations. This comprehensive guide will explore the conversion of 32.5 percent to its decimal form, explaining the process in detail and providing further insights into percentage-decimal conversions. We’ll also delve into practical applications and answer frequently asked questions, ensuring a thorough grasp of this important concept.
Understanding Percentages
Before diving into the conversion, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of one hundred." So, 32.5% means 32.5 parts out of 100. This understanding forms the basis for converting percentages to decimals.
Converting 32.5% to a Decimal
The conversion of a percentage to a decimal involves a simple two-step process:
-
Divide by 100: To convert a percentage to a decimal, divide the percentage value by 100. This is because a percentage is a fraction with a denominator of 100.
-
Remove the Percent Symbol: Once you've divided by 100, remove the percent symbol (%).
Let's apply this to 32.5%:
32.5% ÷ 100 = 0.325
Therefore, 32.5% as a decimal is 0.325.
The Mechanics Behind the Conversion
Mathematically, the conversion can be understood as follows:
-
Percentage as a Fraction: 32.5% can be written as the fraction 32.5/100.
-
Decimal Conversion: Dividing the numerator (32.5) by the denominator (100) yields the decimal equivalent, 0.325.
This process works universally for any percentage. Simply divide the percentage value by 100 to obtain its decimal representation.
Practical Applications of Decimal Equivalents
Understanding the decimal equivalent of percentages is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, tax percentages, and profit margins often requires converting percentages to decimals. For instance, calculating a 32.5% discount on a $100 item would involve multiplying $100 by 0.325 to find the discount amount.
-
Statistics: Many statistical calculations rely on decimal representations of percentages. Probability, data analysis, and hypothesis testing often utilize decimal forms for ease of calculation and interpretation.
-
Science: In scientific fields, expressing proportions and ratios often involves decimal equivalents of percentages. This allows for more precise calculations and comparisons.
-
Everyday Calculations: From calculating tips in restaurants to understanding sale prices in stores, the ability to convert percentages to decimals simplifies many everyday calculations.
Converting Decimals to Percentages
The reverse process, converting a decimal to a percentage, is equally important. This involves multiplying the decimal by 100 and adding the percent symbol.
For example, to convert 0.325 back to a percentage:
0.325 x 100 = 32.5
Adding the percent symbol gives us 32.5%. This demonstrates the inverse relationship between decimals and percentages.
Working with Percentages Greater Than 100%
It’s important to note that percentages can also exceed 100%. This represents a value greater than the whole. For example, 150% is equivalent to 1.5 in decimal form (150 ÷ 100 = 1.5). The same conversion principles apply, even with percentages above 100%.
Dealing with Percentages Less Than 1%
Similarly, percentages can be less than 1%. For instance, 0.5% is equivalent to 0.005 as a decimal (0.5 ÷ 100 = 0.005). Again, the same division method applies, resulting in a decimal value less than 1.
Advanced Applications: Percentage Change and Growth
Understanding decimal equivalents of percentages becomes particularly crucial when dealing with percentage changes or growth rates. For example, if a quantity increases by 32.5%, you would calculate the new value by multiplying the original value by (1 + 0.325) = 1.325. This reflects the original value plus the increase represented as a decimal.
Frequently Asked Questions (FAQ)
Q1: Why is it important to convert percentages to decimals?
A1: Converting percentages to decimals simplifies mathematical calculations. Most calculators and computer programs perform calculations more efficiently with decimals than percentages.
Q2: Can I convert percentages with fractions, such as 32 1/2%?
A2: Yes, you can. First, convert the mixed fraction to a decimal (32 1/2 = 32.5). Then, divide by 100 to obtain the decimal equivalent (0.325).
Q3: What are some common mistakes to avoid when converting percentages to decimals?
A3: A common mistake is forgetting to divide by 100 or incorrectly moving the decimal point. Always remember the process: divide the percentage by 100.
Q4: How do I convert a percentage to a fraction?
A4: To convert a percentage to a fraction, write the percentage as a fraction with a denominator of 100, and then simplify the fraction if possible. For example, 32.5% = 32.5/100 = 65/200 = 13/40
Q5: Are there any online tools to help with percentage-decimal conversions?
A5: While many online calculators can perform these conversions, understanding the underlying principles is crucial for efficient and accurate calculations without reliance on external tools.
Conclusion
Converting 32.5% to its decimal equivalent, 0.325, is a straightforward process requiring division by 100. This seemingly simple conversion is a cornerstone skill with wide-ranging applications across diverse fields. Understanding this process, as well as the reverse conversion from decimal to percentage, empowers you to confidently handle percentage-based calculations in various contexts, from everyday finance to complex scientific applications. Mastering this skill enhances numerical literacy and analytical capabilities, proving invaluable in both academic and professional settings. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
7 3 8 Higher Lower 2 0
Sep 14, 2025
-
70 000 Divided By 12
Sep 14, 2025
-
3 87 As A Decimal
Sep 14, 2025
-
Hormones Are Only Effective In
Sep 14, 2025
-
24 Cm How Many Inches
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 32.5 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.