34x 25 How To Solve
cibeltiagestion
Sep 13, 2025 · 5 min read
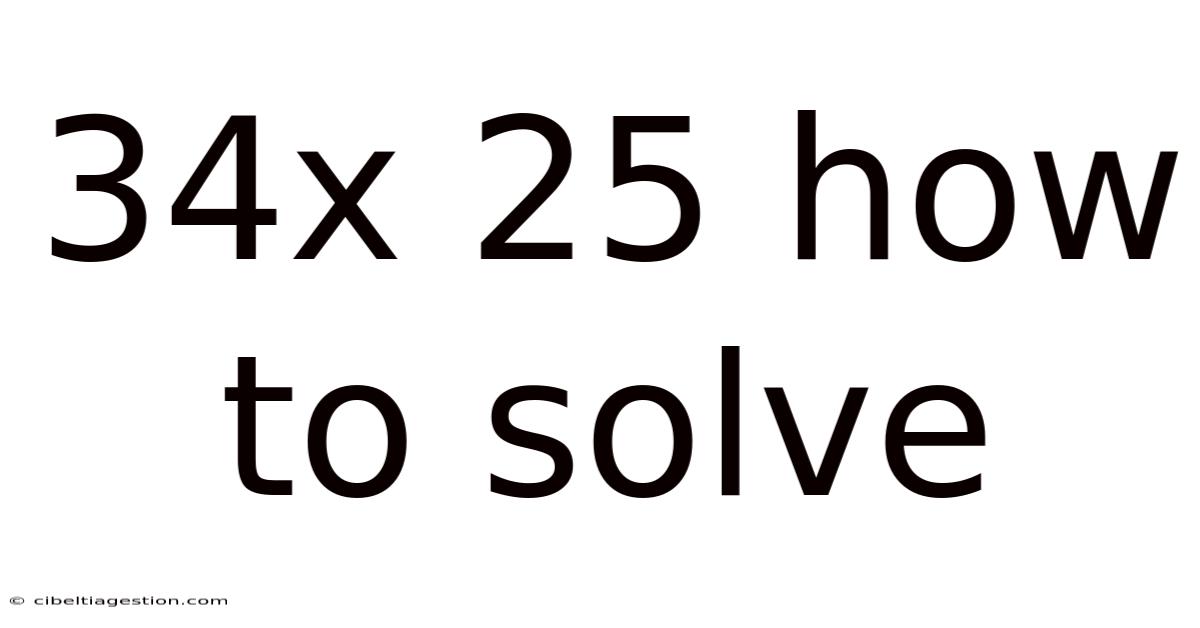
Table of Contents
Mastering Multiplication: A Deep Dive into Solving 34 x 25
This article provides a comprehensive guide to solving the multiplication problem 34 x 25, exploring various methods accessible to different learning styles and mathematical skill levels. We'll move beyond simply providing the answer, delving into the underlying principles and offering multiple approaches to build a solid understanding of multiplication. Understanding these methods will equip you to tackle similar problems with confidence and build a strong foundation in arithmetic. This is particularly useful for students learning multiplication, but also serves as a refresher for adults looking to sharpen their math skills.
Introduction: Why Understanding 34 x 25 Matters
The seemingly simple problem of 34 x 25 represents a fundamental concept in mathematics: multiplication. Mastering multiplication isn't just about getting the right answer; it's about developing a deeper understanding of numerical relationships and building a foundation for more complex mathematical concepts like algebra and calculus. This problem, in particular, provides an excellent opportunity to explore different calculation methods, enhancing your mathematical flexibility and problem-solving skills. Furthermore, understanding the strategies used to solve this problem can be applied to a wide range of multiplication problems, making it a valuable skill to master.
Method 1: The Standard Algorithm (Long Multiplication)
This is the traditional method taught in many schools. It involves multiplying each digit of one number by each digit of the other number and then adding the partial products.
Steps:
-
Set up the problem: Write the numbers vertically, one above the other, aligning the units digits.
34 x 25 ---- -
Multiply by the units digit: Multiply 34 by 5 (the units digit of 25).
34 x 25 ---- 170 (34 x 5 = 170) -
Multiply by the tens digit: Multiply 34 by 20 (the tens digit of 25). Remember to add a zero as a placeholder in the units column because we are multiplying by a multiple of ten.
34 x 25 ---- 170 680 (34 x 20 = 680) -
Add the partial products: Add the two partial products together.
34 x 25 ---- 170 680 ---- 850
Therefore, 34 x 25 = 850
Method 2: Distributive Property
The distributive property states that a(b + c) = ab + ac. We can use this property to break down the multiplication into smaller, easier-to-manage parts.
Steps:
-
Break down 25: Rewrite 25 as (20 + 5).
-
Apply the distributive property: Rewrite the problem as 34 x (20 + 5).
-
Multiply and add: This becomes (34 x 20) + (34 x 5).
-
Calculate: (34 x 20) = 680 and (34 x 5) = 170.
-
Add the results: 680 + 170 = 850
This method demonstrates a key mathematical principle and can be particularly helpful in understanding the logic behind multiplication.
Method 3: Using Quarters (Fractions)
This method leverages the fact that 25 is one-quarter of 100.
Steps:
-
Multiply by 100: Multiply 34 by 100: 34 x 100 = 3400
-
Divide by 4: Since 25 is one-fourth of 100, divide the result by 4: 3400 / 4 = 850
This approach is quick and efficient once you understand the relationship between 25 and 100.
Method 4: Mental Math Techniques
For those comfortable with mental arithmetic, several strategies can streamline the calculation.
-
Breaking down 34: Think of 34 as (30 + 4). Then, multiply each part by 25: (30 x 25) + (4 x 25) = 750 + 100 = 850
-
Doubling and Halving: Double 34 (to get 68) and halve 25 (to get 12.5). Then, multiply 68 by 12.5. This might seem more complex at first, but with practice, it can be done mentally. Alternatively, halve 34 (17) and double 25 (50). Then multiply 17 x 50 which is easier. 17 x 50 = 850
Method 5: Using a Calculator (For Verification or When Time is Limited)
While not a method for developing mathematical understanding, a calculator can be a useful tool for checking answers or when speed is critical. Simply enter "34 x 25" into a calculator to obtain the answer: 850
Explaining the Scientific Basis: Properties of Multiplication
The success of all these methods rests on the fundamental properties of multiplication:
-
Commutative Property: The order of the numbers doesn't affect the product (a x b = b x a). This means 34 x 25 is the same as 25 x 34.
-
Associative Property: When multiplying more than two numbers, the grouping doesn't matter ((a x b) x c = a x (b x c)). This is relevant when breaking down the numbers into smaller parts.
-
Distributive Property: As demonstrated earlier, this property allows us to break down complex multiplication into simpler steps.
Understanding these properties provides a deeper understanding of why these various methods work.
Frequently Asked Questions (FAQ)
-
Q: Is there only one correct way to solve 34 x 25?
A: No. There are several valid methods, each offering a different approach to the problem. The best method depends on your comfort level with various mathematical concepts and your personal preference.
-
Q: Which method is the fastest?
A: The fastest method often depends on individual skill and familiarity with the methods. For some, the mental math techniques or the quarters method might be quickest. For others, the standard algorithm might be more efficient.
-
Q: Why is it important to learn multiple methods?
A: Learning multiple methods enhances your mathematical flexibility and problem-solving skills. It also provides a deeper understanding of the underlying mathematical principles. Furthermore, different methods may be more efficient in different contexts.
-
Q: What if I'm struggling with one of these methods?
A: Practice is key. Try each method repeatedly, focusing on understanding the steps involved. If you continue to struggle, seek assistance from a teacher, tutor, or online resources.
Conclusion: Mastering Multiplication – A Journey, Not a Destination
Solving 34 x 25 is more than just finding the answer; it's about developing a deep understanding of multiplication and its underlying principles. By exploring various approaches – the standard algorithm, distributive property, using fractions (quarters), mental math, and even using a calculator for verification – you gain a multifaceted understanding of this fundamental mathematical operation. The journey to mastering multiplication is about building confidence and developing problem-solving skills that extend far beyond this single problem. Remember, consistent practice and a willingness to explore different methods are key to achieving mathematical fluency. Keep practicing, and you’ll find that multiplication becomes progressively easier and more intuitive. The ability to quickly and accurately perform multiplication is a valuable skill applicable to countless real-world situations and further mathematical studies.
Latest Posts
Latest Posts
-
Whats 20 Percent Of 40
Sep 14, 2025
-
Antarctica Governing The Icy Continent
Sep 14, 2025
-
Unit Conversion Mg L To Ppm
Sep 14, 2025
-
Molecular Mass Of Magnesium Hydroxide
Sep 14, 2025
-
Charles Bonnet Syndrome Icd 10
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 34x 25 How To Solve . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.