3x 2 X 2 2
cibeltiagestion
Sep 08, 2025 · 6 min read
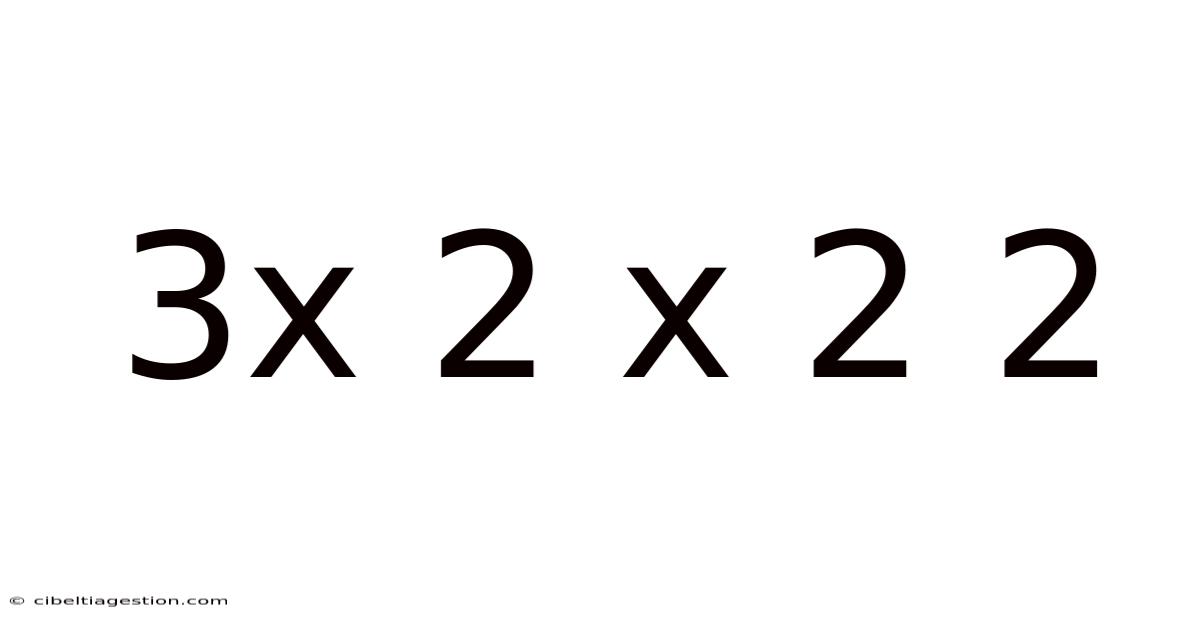
Table of Contents
Decoding the Enigma: Exploring the Mathematical and Logical Implications of "3 x 2 x 2 x 2"
The seemingly simple expression "3 x 2 x 2 x 2" presents a fascinating opportunity to explore fundamental mathematical concepts, delve into different approaches to problem-solving, and even touch upon the broader implications of numerical patterns and their applications in various fields. This article will dissect this expression, explaining its calculation, exploring its potential interpretations beyond simple multiplication, and highlighting its relevance in fields like computer science and combinatorics.
Introduction: Understanding the Basics
At its core, "3 x 2 x 2 x 2" is a straightforward multiplication problem. It involves multiplying the number 3 by 2 four times. While the calculation itself is elementary, its underlying structure and potential interpretations open up a wide range of mathematical and logical explorations. We will systematically break down this seemingly simple expression, revealing its depth and versatility.
1. Direct Calculation and Order of Operations
The most immediate approach is to perform the calculation directly, following the order of operations (PEMDAS/BODMAS). Since there are only multiplication operations, the order doesn't matter; we can perform the multiplications from left to right:
- 3 x 2 = 6
- 6 x 2 = 12
- 12 x 2 = 24
Therefore, the solution to 3 x 2 x 2 x 2 is 24. This straightforward approach emphasizes the fundamental nature of multiplication as repeated addition. Each multiplication step represents adding the previous result to itself as many times as indicated by the multiplier.
2. Exponents and Power of Two
We can also approach this problem using exponents. Notice that the expression contains three 2s multiplied together, which can be represented as 2³. Therefore, the calculation can be rewritten as:
3 x (2 x 2 x 2) = 3 x 2³
Since 2³ = 8, the calculation becomes:
3 x 8 = 24
This approach highlights the concept of exponentiation and its connection to repeated multiplication. Understanding exponents is crucial in many areas of mathematics, especially in algebra, calculus, and more advanced mathematical disciplines. The ability to recognize and apply exponents simplifies calculations and reveals underlying mathematical patterns.
3. Factorization and Prime Numbers
The result, 24, can be further analyzed through factorization. Factorization involves expressing a number as a product of its prime factors. The prime factorization of 24 is 2³ x 3. This highlights the fundamental building blocks of the number 24 and demonstrates the interconnectedness of different mathematical concepts. Prime factorization is a fundamental tool used in cryptography, number theory, and various other mathematical fields.
4. Combinatorial Interpretations
Beyond the purely numerical aspect, the expression "3 x 2 x 2 x 2" can be interpreted within the context of combinatorics. Consider a scenario where we have three choices for the first selection, and then two choices for each of the subsequent three selections. This could represent various real-world situations, such as:
-
Choosing items from a menu: Imagine selecting a main course (3 options), a side dish (2 options), a drink (2 options), and a dessert (2 options). The total number of possible meal combinations would be 3 x 2 x 2 x 2 = 24.
-
Arranging items: Imagine arranging three different colored balls in a sequence, where each ball can be one of two different sizes. The total number of arrangements would again be 24.
These combinatorial interpretations showcase the practical application of multiplication and demonstrate how numerical expressions can model real-world scenarios involving choices and arrangements. Combinatorics is a vast field with applications in probability, statistics, and computer science.
5. Applications in Computer Science
In computer science, binary numbers (based on powers of 2) are fundamental. The repeated multiplication by 2 in the expression "3 x 2 x 2 x 2" is directly relevant to binary operations and data representation. Each multiplication by 2 represents a shift to the left in a binary number, effectively multiplying the number by a power of 2. This understanding is crucial for optimizing algorithms and understanding how data is stored and manipulated within computer systems.
6. Logical Implications and Problem Solving
The problem of calculating "3 x 2 x 2 x 2" may seem trivial, but it underscores the importance of methodical problem-solving. By approaching the problem from different perspectives—direct calculation, exponents, factorization, and combinatorial interpretations—we gain a deeper understanding of the underlying mathematical principles and enhance our problem-solving skills. This analytical approach is transferable to more complex mathematical and real-world problems.
7. Expanding the Concept: Generalizing the Expression
We can generalize the expression to explore a broader pattern. Instead of "3 x 2 x 2 x 2," consider the more general expression: a x b x b x b, where 'a' and 'b' are any numbers. This allows us to explore the impact of changing the initial value ('a') and the repeated multiplier ('b'). Analyzing this generalized expression helps in understanding the broader mathematical relationships and patterns involved.
8. Beyond Arithmetic: Algebraic Representation
We can represent the expression algebraically as 3 * 2<sup>3</sup>. This allows us to manipulate the expression algebraically, substituting different values for 3 and 2, and explore the resultant changes in the outcome. This algebraic representation is powerful as it provides a concise and generalizable way to express the mathematical relationship.
9. Error Analysis and Computational Precision
While the calculation of "3 x 2 x 2 x 2" is straightforward, it's worthwhile to consider potential sources of error in more complex calculations. In computer programming, for instance, floating-point arithmetic can introduce small inaccuracies. Understanding these potential errors is vital for ensuring the accuracy and reliability of computational results.
10. Further Explorations and Related Topics
The simple expression "3 x 2 x 2 x 2" acts as a gateway to several more advanced topics, such as:
- Number Theory: Exploring the properties of numbers, prime factorization, and divisibility rules.
- Abstract Algebra: Studying mathematical structures and their properties, such as groups and rings.
- Discrete Mathematics: Dealing with finite sets, combinatorics, graph theory, and their applications in computer science.
- Calculus: Understanding concepts such as limits, derivatives, and integrals, which build upon fundamental arithmetic operations.
Conclusion: The Unsurprising Depth of Simplicity
The seemingly simple expression "3 x 2 x 2 x 2" reveals a surprisingly rich mathematical landscape. From basic arithmetic to advanced concepts like combinatorics and algebraic representation, this expression provides a valuable learning opportunity. By approaching the problem from multiple perspectives and exploring its wider implications, we gain a deeper appreciation for the interconnectedness of mathematical concepts and the power of analytical thinking. The seemingly straightforward calculation underscores the importance of fundamental mathematical skills and the continuous journey of learning and exploration within the fascinating world of numbers. This understanding extends far beyond the simple act of multiplication, touching upon crucial concepts in numerous scientific and technological fields.
Latest Posts
Latest Posts
-
A Rectangular Shaped Sign Is
Sep 08, 2025
-
What Does Gi Stand For
Sep 08, 2025
-
Shorthand Electron Configuration For Lead
Sep 08, 2025
-
Who Were The Viet Cong
Sep 08, 2025
-
Meaning Of Dict Root Word
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 X 2 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.