4 1/4 - 2 2/4
cibeltiagestion
Sep 07, 2025 · 6 min read
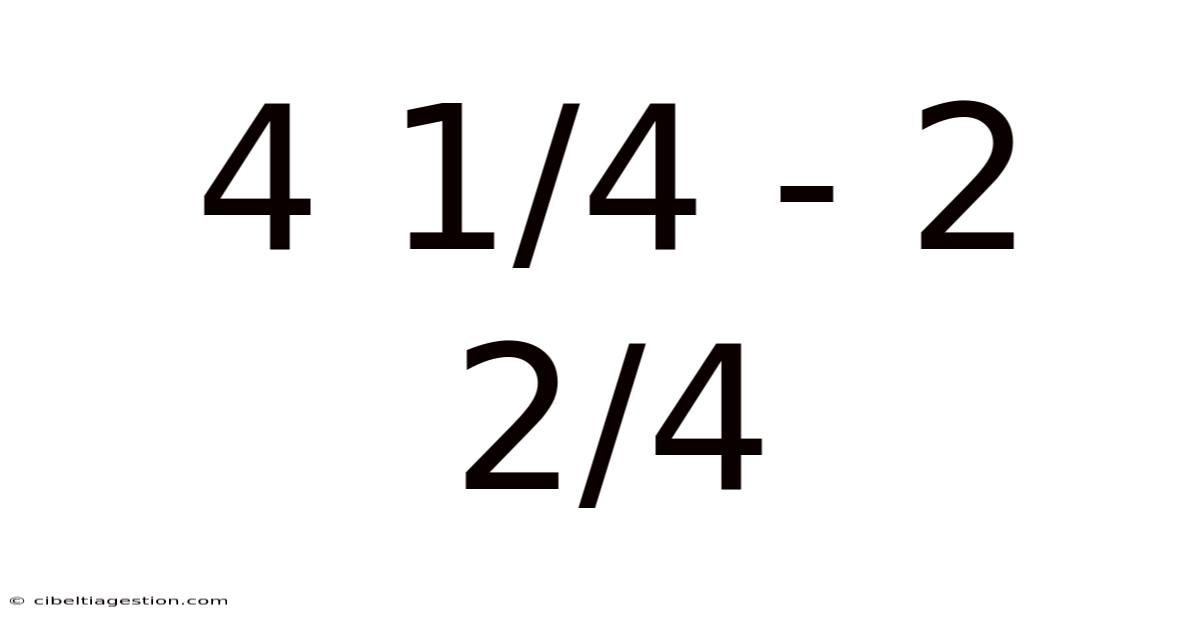
Table of Contents
Decoding Fractions: A Comprehensive Guide to Solving 4 1/4 - 2 2/4
This article provides a step-by-step guide on how to solve the subtraction problem 4 1/4 - 2 2/4, explaining the underlying principles of fraction subtraction and offering helpful strategies for similar problems. Understanding fraction subtraction is a crucial skill in mathematics, applicable in various fields from cooking and construction to advanced calculus. This guide aims to demystify the process, building a strong foundational understanding for all learners.
Understanding Fractions: A Quick Refresher
Before diving into the subtraction problem, let's quickly recap the basics of fractions. A fraction represents a part of a whole. It's composed of two parts: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 1/4, the denominator (4) means the whole is divided into four equal parts, and the numerator (1) represents one of those parts. In mixed numbers like 4 1/4, we have a whole number (4) combined with a fraction (1/4). This signifies four whole units and one-quarter of another unit.
Solving 4 1/4 - 2 2/4: A Step-by-Step Approach
The problem 4 1/4 - 2 2/4 presents a common challenge in fraction subtraction: the fraction being subtracted is larger than the fraction being subtracted from. Let's break down the solution methodically:
Step 1: Recognizing the Issue
Observe that we're attempting to subtract 2/4 from 1/4. This isn't directly possible because 2/4 is larger than 1/4. This requires us to borrow from the whole number part.
Step 2: Borrowing from the Whole Number
We borrow 1 from the whole number 4, leaving us with 3. This borrowed 1 is then converted into a fraction with the same denominator as the existing fractions (4 in this case). Therefore, 1 becomes 4/4.
Step 3: Rewriting the Equation
Our equation now transforms from 4 1/4 - 2 2/4 to (3 + 4/4) + 1/4 - 2 2/4. Combining the fractions, we get 3 5/4 - 2 2/4.
Step 4: Subtracting the Whole Numbers and Fractions Separately
Now we can subtract the whole numbers and the fractions independently:
- Whole numbers: 3 - 2 = 1
- Fractions: 5/4 - 2/4 = 3/4
Step 5: Combining the Results
Combining the results from the whole number and fraction subtractions, we get the final answer: 1 3/4
Therefore, 4 1/4 - 2 2/4 = 1 3/4
Alternative Method: Converting to Improper Fractions
Another effective method involves converting the mixed numbers into improper fractions before subtracting. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
Step 1: Convert Mixed Numbers to Improper Fractions
- 4 1/4: To convert this, multiply the whole number (4) by the denominator (4), add the numerator (1), and place the result over the original denominator: (4 x 4) + 1 = 17/4
- 2 2/4: Similarly, (2 x 4) + 2 = 10/4
Step 2: Perform the Subtraction
The problem now becomes 17/4 - 10/4. Since the denominators are the same, we can simply subtract the numerators: 17 - 10 = 7. The denominator remains the same.
Step 3: Simplify the Result (If Necessary)
The result is 7/4. This is an improper fraction. To convert it back to a mixed number, divide the numerator (7) by the denominator (4). The quotient (1) becomes the whole number, and the remainder (3) becomes the numerator of the fraction. The denominator remains the same. Thus, 7/4 = 1 3/4
Therefore, using this method also yields the answer: 1 3/4
Understanding the Concept of "Borrowing"
The act of "borrowing" in fraction subtraction might seem arbitrary at first, but it's a crucial step rooted in the fundamental concept of representing quantities. When we borrow 1 from the 4, we're essentially breaking down one whole unit into smaller parts (4/4 in this case) that are compatible with the existing fractions. This allows for a consistent and accurate subtraction process.
Practical Applications and Real-World Examples
Understanding fraction subtraction extends beyond theoretical exercises. Here are some real-world scenarios where this skill comes into play:
- Cooking: Recipes often require precise measurements. If a recipe calls for 4 1/4 cups of flour and you've already used 2 2/4 cups, knowing how to subtract fractions helps determine the remaining amount.
- Construction: Precise measurements are essential in construction, particularly when dealing with lengths and materials. Calculating remaining material or adjusting dimensions often necessitates fraction subtraction.
- Sewing/Tailoring: When working with patterns and fabrics, accurate measurements are crucial. Subtracting fractions helps determine the amount of fabric needed or left over.
- Financial calculations: Many financial calculations, like determining the difference between budgets or calculating discounts, require a strong understanding of fraction arithmetic.
Frequently Asked Questions (FAQ)
Q1: What if the denominators are different?
A1: If the denominators are different, you must first find a common denominator before performing the subtraction. This involves finding the least common multiple (LCM) of the denominators. Then, convert both fractions to equivalent fractions with the common denominator.
Q2: Can I use a calculator for fraction subtraction?
A2: While calculators can be helpful for more complex calculations, understanding the underlying principles of fraction subtraction is crucial for developing mathematical reasoning skills. Practicing manual calculations strengthens your understanding and problem-solving abilities.
Q3: What are some common mistakes to avoid in fraction subtraction?
A3: Common mistakes include forgetting to find a common denominator when subtracting fractions with different denominators, incorrectly borrowing from the whole number, and not simplifying the final answer.
Q4: How can I improve my skills in fraction subtraction?
A4: Practice regularly! Start with simpler problems and gradually increase the complexity. Use visual aids like diagrams or fraction bars to help you visualize the process. Also, seek help from teachers or tutors if you encounter difficulties.
Conclusion
Subtracting fractions, even seemingly simple problems like 4 1/4 - 2 2/4, requires a thorough understanding of fractional representation and the principles of borrowing. Mastering this skill is fundamental to success in mathematics and its countless applications in everyday life. By following the steps outlined and practicing regularly, you can confidently tackle fraction subtraction problems and enhance your mathematical proficiency. Remember to always double-check your work and consider using alternative methods to verify your answer. Through consistent practice and a firm grasp of the underlying concepts, you'll build a strong foundation in arithmetic and develop essential problem-solving skills.
Latest Posts
Latest Posts
-
Convert 65 F To C
Sep 08, 2025
-
How Can Diversity Affect Lawmaking
Sep 08, 2025
-
Toma El Examen De Biologia
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 4 1/4 - 2 2/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.