4 Divided By 2 5
cibeltiagestion
Sep 02, 2025 · 5 min read
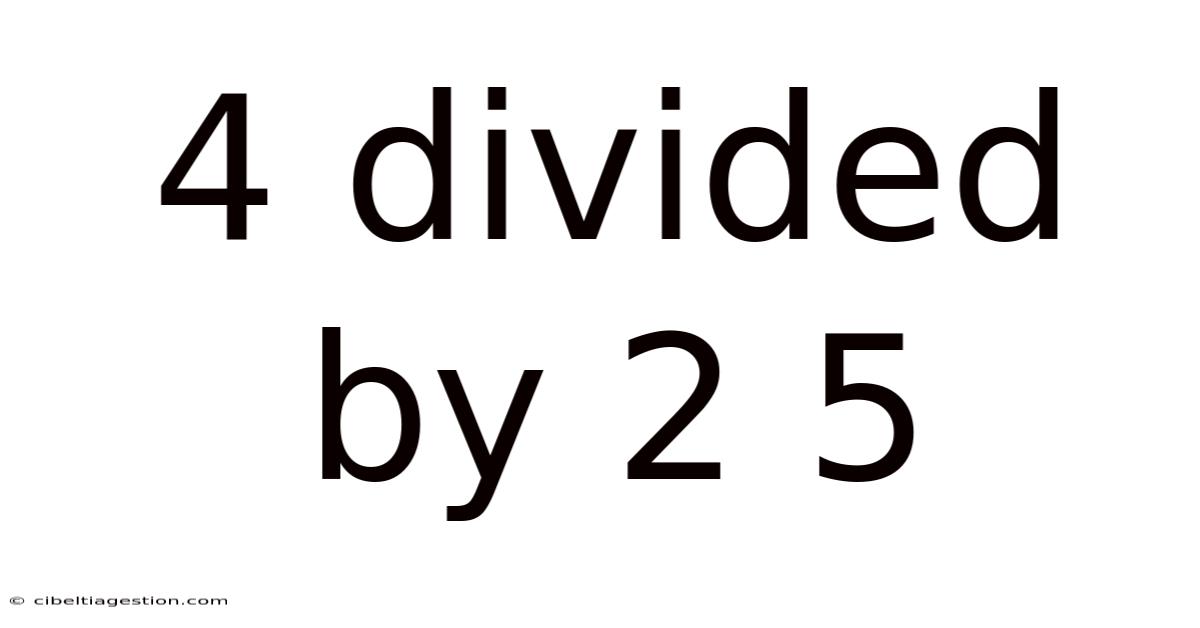
Table of Contents
Decoding 4 Divided by 2/5: A Deep Dive into Fraction Division
Many people find fractions intimidating, and division involving fractions can seem particularly daunting. However, understanding how to solve problems like "4 divided by 2/5" is crucial for a solid grasp of arithmetic and algebra. This article will break down this seemingly complex calculation step-by-step, exploring the underlying principles and providing a thorough understanding of the process. We'll also tackle common misconceptions and offer practical applications to solidify your learning. By the end, you'll confidently tackle similar fraction division problems.
Understanding the Problem: 4 ÷ 2/5
The problem "4 divided by 2/5" asks: "How many times does 2/5 fit into 4?" This phrasing helps visualize the process. We aren't simply dividing a whole number by a fraction; we're determining how many smaller parts (2/5) are contained within a larger whole (4).
Method 1: The "Keep, Change, Flip" Method (aka Reciprocal Method)
This is the most common and arguably the easiest method for dividing fractions. It relies on the concept of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/5 is 5/2.
Here's how to apply the "Keep, Change, Flip" method to solve 4 ÷ 2/5:
-
Keep: Keep the first number (the dividend) as it is: 4.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip the second number (the divisor) – find its reciprocal. The reciprocal of 2/5 is 5/2.
Now, the problem becomes: 4 × 5/2
-
Multiply: Multiply the numerators (top numbers) together: 4 × 5 = 20
-
Multiply: Multiply the denominators (bottom numbers) together: 1 × 2 = 2 (Remember that 4 can be written as 4/1)
-
Simplify: The result is 20/2. This simplifies to 10.
Therefore, 4 divided by 2/5 equals 10.
Method 2: Understanding the Concept Through Visual Representation
Imagine you have 4 pizzas. Each pizza is divided into fifths (5 slices). The problem asks how many 2/5 slices (two slices out of five) you can get from the four pizzas.
-
Total slices: Since each pizza has 5 slices, four pizzas have 4 × 5 = 20 slices.
-
Groups of 2/5: We want to find how many groups of two slices we can make from the 20 slices.
-
Number of groups: 20 slices / 2 slices/group = 10 groups
This visual method confirms that 4 divided by 2/5 equals 10.
Method 3: Converting to Improper Fractions
This method involves converting the whole number into a fraction before performing the division.
-
Convert to a fraction: Express the whole number 4 as a fraction: 4/1.
-
Divide the fractions: Now the problem becomes (4/1) ÷ (2/5).
-
Keep, Change, Flip: Apply the "Keep, Change, Flip" method: (4/1) × (5/2).
-
Multiply: Multiply the numerators: 4 × 5 = 20
-
Multiply: Multiply the denominators: 1 × 2 = 2
-
Simplify: Simplify the fraction 20/2 to 10.
This method achieves the same result as the previous methods.
Why These Methods Work: A Deeper Mathematical Explanation
The "Keep, Change, Flip" method isn't just a trick; it's a consequence of the rules of fraction division. Division is the inverse operation of multiplication. To divide by a fraction, we essentially multiply by its reciprocal.
Consider the general case: a ÷ (b/c)
This can be rewritten as: a × (c/b)
This is because dividing by a fraction is equivalent to multiplying by its multiplicative inverse (reciprocal). The reciprocal of a fraction, b/c, is c/b. This mathematical principle underpins the "Keep, Change, Flip" method.
Addressing Common Misconceptions
-
Incorrect order of operations: It's crucial to remember the order of operations (PEMDAS/BODMAS). In this case, the division operation takes precedence before any other operation.
-
Incorrectly flipping both fractions: Only the divisor (the fraction you're dividing by) should be flipped, not the dividend (the number being divided).
-
Forgetting to simplify: Always simplify the resulting fraction to its lowest terms for the most accurate answer.
Real-World Applications
Understanding fraction division is essential in various real-world situations:
-
Cooking and baking: Scaling recipes up or down requires dividing and multiplying fractions.
-
Construction and engineering: Calculating precise measurements and quantities often involves fractions.
-
Sewing and tailoring: Cutting fabric and adjusting patterns requires accurate fractional calculations.
-
Finance and budgeting: Dividing resources and managing finances often involves fractional amounts.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this? A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for problem-solving in more complex scenarios.
-
Q: What if the whole number is negative? A: Treat the negative sign as part of the numerator. The process remains the same. For example, -4 ÷ 2/5 would be -4/1 × 5/2 = -20/2 = -10.
-
Q: What if the fraction is a mixed number? A: Convert the mixed number to an improper fraction before applying the "Keep, Change, Flip" method. For example, 4 ÷ 2 1/2 becomes 4 ÷ 5/2, which then becomes 4/1 × 2/5 = 8/5 = 1 3/5.
-
Q: What if both numbers are fractions? A: The "Keep, Change, Flip" method still applies.
Conclusion
Dividing by a fraction, even a seemingly simple one like 2/5, might seem intimidating at first. However, by understanding the underlying principles and employing the "Keep, Change, Flip" method or the visual approach, you can easily master this skill. Remember to always convert mixed numbers into improper fractions and simplify your final answer. With practice and a grasp of the concepts, you’ll not only solve these problems confidently but also apply this knowledge to more advanced mathematical concepts. Mastering fraction division is a crucial step towards a more comprehensive understanding of mathematics and its applications in the real world.
Latest Posts
Latest Posts
-
Hz To Rad Per Sec
Sep 02, 2025
-
What Continent Is Egypt In
Sep 02, 2025
-
Which Example Best Demonstrates Irony
Sep 02, 2025
-
Did Dodo Birds Eat Rocks
Sep 02, 2025
-
Union And Intersection Of Intervals
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.