4x 3y - 4y 10x
cibeltiagestion
Sep 15, 2025 · 5 min read
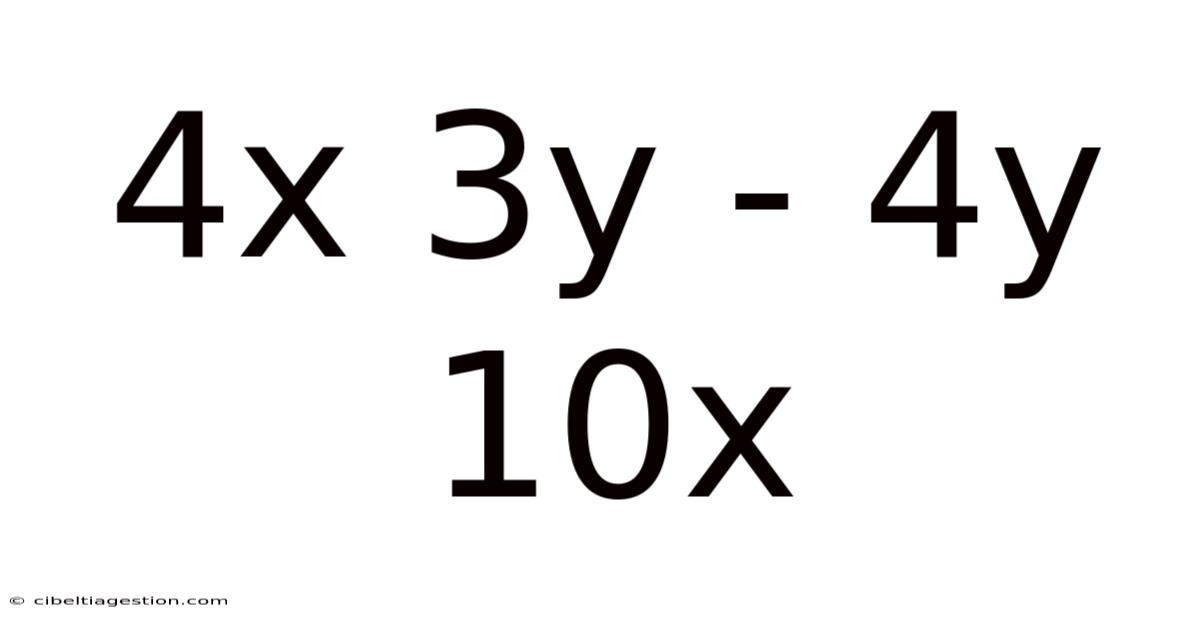
Table of Contents
Unveiling the Mysteries: A Deep Dive into 4x + 3y - 4y + 10x
This article explores the algebraic expression 4x + 3y - 4y + 10x, guiding you through simplification, understanding its components, and exploring its potential applications. Whether you're a student grappling with algebra or simply curious about mathematical manipulation, this comprehensive guide will equip you with the knowledge and confidence to tackle similar expressions. We'll cover the fundamental concepts, provide step-by-step solutions, and even delve into more advanced considerations. This exploration will go beyond simple simplification, touching upon the broader context of linear equations and their real-world implications.
Introduction: Deconstructing the Expression
The expression 4x + 3y - 4y + 10x represents a linear combination of two variables, x and y. Linear combinations are fundamental building blocks in algebra and have far-reaching applications in various fields, including physics, economics, and computer science. Understanding how to simplify and manipulate these expressions is crucial for solving equations, modeling real-world scenarios, and progressing to more complex mathematical concepts. Our primary goal here is to simplify the given expression and understand the underlying principles involved.
Step-by-Step Simplification: A Practical Approach
Simplifying algebraic expressions involves combining like terms. Like terms are terms that have the same variables raised to the same powers. In our expression, 4x and 10x are like terms, as are 3y and -4y. Let's break down the simplification process step-by-step:
-
Identify Like Terms: The expression contains two sets of like terms:
- x terms: 4x and 10x
- y terms: 3y and -4y
-
Combine Like Terms: Add or subtract the coefficients (the numbers in front of the variables) of the like terms:
- For the x terms: 4x + 10x = 14x
- For the y terms: 3y - 4y = -y
-
Rewrite the Simplified Expression: After combining the like terms, the simplified expression becomes: 14x - y
Therefore, the simplified form of 4x + 3y - 4y + 10x is 14x - y. This simplified form is equivalent to the original expression, meaning it represents the same value for any given values of x and y.
Deeper Understanding: The Concept of Linear Equations
The simplified expression, 14x - y, represents a linear equation if we set it equal to a constant value. For instance, 14x - y = 7 is a linear equation. Linear equations are characterized by their straight-line graphs when plotted on a Cartesian coordinate system. The expression's variables (x and y) represent coordinates, and the equation defines the relationship between these coordinates along a straight line.
-
Slope and Intercept: Linear equations are often expressed in the slope-intercept form: y = mx + b, where 'm' is the slope and 'b' is the y-intercept. Our simplified expression can be rearranged into this form: y = 14x - 7 (if we set the expression equal to 7, for example). In this case, the slope (m) is 14, indicating a steep positive slope, and the y-intercept (b) is -7, meaning the line crosses the y-axis at -7.
-
Graphical Representation: Plotting the linear equation on a graph allows for a visual understanding of the relationship between x and y. Each point (x, y) that satisfies the equation lies on the line. The slope dictates the steepness and direction of the line, while the y-intercept determines where it intersects the y-axis.
-
Applications of Linear Equations: Linear equations are widely used to model various real-world phenomena. Examples include:
- Calculating Costs: The total cost (y) of producing a certain number of items (x) can often be represented by a linear equation.
- Predicting Trends: Linear equations can be used to predict future values based on existing data, like projecting sales revenue or population growth.
- Analyzing Relationships: Linear equations help to analyze the relationships between two variables, such as distance and time, or temperature and pressure.
Beyond Simplification: Exploring Advanced Concepts
While simplifying the algebraic expression is a fundamental step, understanding its implications within a broader mathematical context is equally crucial. Here are some advanced concepts to consider:
-
Systems of Linear Equations: Our simplified expression, when set equal to a constant, becomes a single linear equation. However, real-world problems often involve systems of linear equations, where multiple equations with multiple variables need to be solved simultaneously. Methods like substitution, elimination, and matrix methods are used to find solutions for these systems.
-
Linear Programming: Linear programming is an optimization technique used to find the best possible solution (maximum or minimum) for a linear objective function subject to linear constraints. The simplified expression could represent a component within a larger linear programming problem.
-
Vectors and Matrices: In linear algebra, the expression can be represented as a vector or a component of a matrix. This opens up avenues for more sophisticated mathematical manipulations using vector operations and matrix algebra.
Frequently Asked Questions (FAQ)
Q: What if the expression had more variables?
A: The same principles apply. You would group like terms based on their variables and exponents and combine them accordingly. For example, 2x + 5y - x + 3z + 2y would simplify to x + 7y + 3z.
Q: Can I solve for x or y without knowing the other variable's value?
A: No, you cannot solve for a specific value of x or y unless the expression is set equal to a constant, forming a linear equation. You would need an additional equation to create a system of equations, allowing you to solve for both x and y.
Q: What are some common mistakes to avoid when simplifying algebraic expressions?
A: Common mistakes include:
- Incorrectly combining unlike terms: Remember to only combine terms with the same variables raised to the same powers.
- Errors in signs: Pay close attention to positive and negative signs when adding and subtracting terms.
- Forgetting to distribute: If there are parentheses involved, make sure to distribute any coefficients properly before combining like terms.
Conclusion: Mastering the Fundamentals and Beyond
Simplifying the algebraic expression 4x + 3y - 4y + 10x to 14x - y is just the beginning. This exercise showcases the fundamental principles of algebraic manipulation, laying the groundwork for more complex mathematical concepts. Understanding linear equations, their graphical representations, and their applications in various fields broadens your mathematical perspective. The journey from simplifying a simple expression to understanding its role within broader mathematical frameworks underscores the importance of building a solid foundation in algebra. By mastering these fundamental concepts, you equip yourself with the tools to tackle more advanced mathematical challenges and unlock the power of mathematical reasoning in numerous fields. Remember, consistent practice and a curious mindset are key to mastering algebra and unlocking its many applications.
Latest Posts
Latest Posts
-
210 Degrees Celsius To Fahrenheit
Sep 15, 2025
-
Greg Tossed A Number Cube
Sep 15, 2025
-
How To Find Frequency Stats
Sep 15, 2025
-
Ounces In 750 Ml Bottle
Sep 15, 2025
-
10 000 Pounds To Tons
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 4x 3y - 4y 10x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.