5 8 As A Percent
cibeltiagestion
Sep 10, 2025 · 6 min read
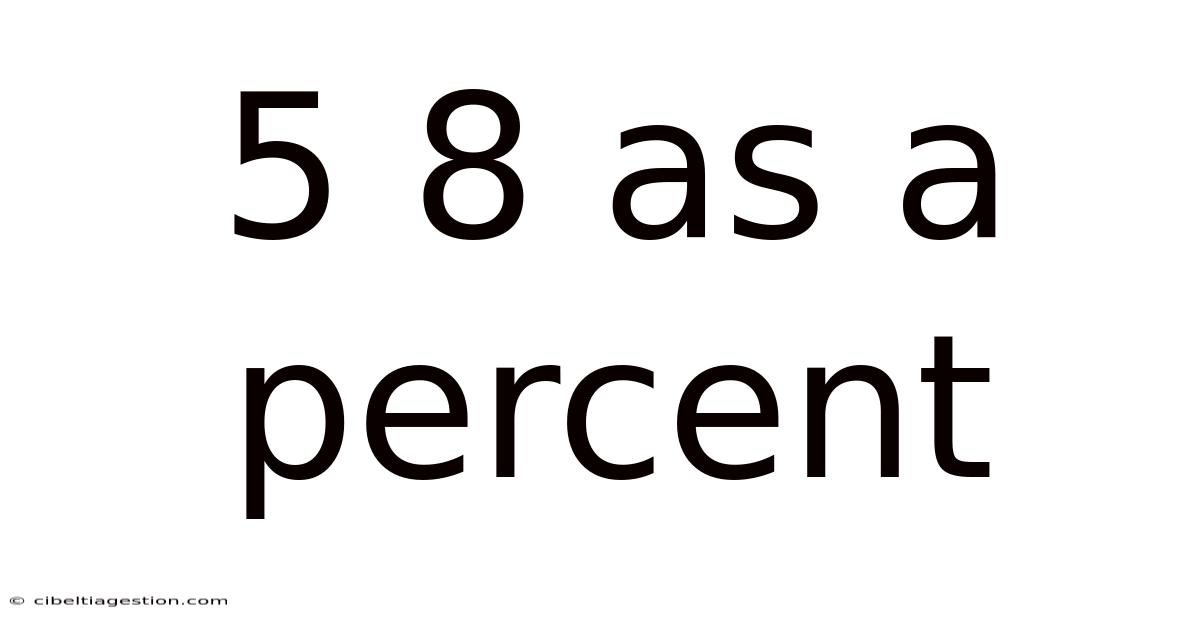
Table of Contents
Decoding 5/8 as a Percentage: A Comprehensive Guide
Understanding fractions and percentages is fundamental to various aspects of life, from calculating discounts in a store to comprehending financial reports. This article dives deep into converting the fraction 5/8 into a percentage, explaining the process step-by-step and exploring related mathematical concepts. We'll cover the method, the rationale behind it, and answer frequently asked questions to ensure a complete understanding of this seemingly simple yet crucial conversion. Learning this skill will empower you to confidently tackle similar problems and build a stronger foundation in mathematics.
Understanding Fractions and Percentages
Before we delve into converting 5/8 to a percentage, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 5/8, 5 is the numerator and 8 is the denominator. This means we have 5 parts out of a total of 8 equal parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It indicates how many parts out of 100 constitute a particular proportion. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2. Percentages are widely used to express proportions and ratios in a standardized and easily understandable format.
Converting 5/8 to a Percentage: The Method
Converting a fraction to a percentage involves two main steps:
Step 1: Convert the Fraction to a Decimal
To convert the fraction 5/8 to a decimal, we divide the numerator (5) by the denominator (8):
5 ÷ 8 = 0.625
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.625 x 100 = 62.5
Therefore, 0.625 is equivalent to 62.5%.
Thus, 5/8 as a percentage is 62.5%.
A Deeper Dive into the Conversion Process
The conversion process relies on the fundamental relationship between fractions, decimals, and percentages. They all represent proportions, but in different formats. Let's break down why the steps work:
-
Fraction to Decimal: Division is the core operation here. A fraction inherently represents a division problem. The numerator is divided by the denominator to find the decimal equivalent. This decimal represents the fraction's value as a part of one whole unit.
-
Decimal to Percentage: Multiplication by 100 scales the decimal value to represent a proportion out of 100. Percentage is essentially a decimal expressed as a part of 100. Multiplying by 100 shifts the decimal point two places to the right, effectively expressing the value as a proportion of 100.
The whole process hinges on the equivalence of different representational forms. The fraction 5/8, the decimal 0.625, and the percentage 62.5% all convey the same proportional value; they simply use different notations to express it.
Practical Applications of Converting 5/8 to a Percentage
Understanding the conversion of 5/8 to 62.5% has practical implications across many fields:
-
Business and Finance: Calculating profits, losses, discounts, interest rates, and market shares frequently involve converting fractions to percentages for easier comprehension and comparison. A 62.5% profit margin, for example, is easily understood and quickly compared to other percentages.
-
Science and Engineering: Representing experimental results, statistical data, and probability often uses percentages for clear and concise communication. If 5 out of 8 experiments yield a positive result, reporting it as a 62.5% success rate offers a clear picture.
-
Everyday Life: Discount calculations, recipe scaling, and even understanding survey results involve percentage calculations. Knowing that 5/8 is equivalent to 62.5% helps in quickly estimating the value of discounts or proportions in daily scenarios.
Exploring Related Fraction-to-Percentage Conversions
Understanding the conversion of 5/8 to a percentage allows for a better understanding of similar conversions. Let's explore a few related examples:
-
1/8 as a Percentage: Following the same process, 1/8 is equivalent to 0.125 or 12.5%. This helps in understanding the proportional relationships between different fractions with the same denominator.
-
3/8 as a Percentage: Similarly, 3/8 translates to 0.375 or 37.5%. This pattern reinforces the relationship between the numerator's value and the resulting percentage.
-
7/8 as a Percentage: Finally, 7/8 converts to 0.875 or 87.5%. Observing this range of values (12.5%, 37.5%, 62.5%, 87.5%) with increments of 25% strengthens the understanding of the overall proportional concept.
Mathematical Proof and Verification
To verify our result (5/8 = 62.5%), we can use a simple algebraic approach:
-
Start with the fraction: 5/8
-
Convert to a decimal: 5 ÷ 8 = 0.625
-
Convert to a percentage: 0.625 * 100 = 62.5%
This method mathematically confirms the equivalence between the fraction 5/8 and the percentage 62.5%. The conversion process is consistent and verifiable through basic arithmetic operations.
Frequently Asked Questions (FAQs)
Q1: Can I use a calculator to convert 5/8 to a percentage?
A1: Absolutely! Most calculators have a division function and can easily handle the conversion from fraction to decimal and then to percentage. Simply divide 5 by 8 and then multiply the result by 100.
Q2: Are there other ways to convert a fraction to a percentage?
A2: Yes, you could also find an equivalent fraction with a denominator of 100. While this method is feasible for some fractions, it's often less efficient than the direct decimal-to-percentage conversion method.
Q3: What if the fraction results in a repeating decimal?
A3: If the fraction results in a repeating decimal, you'll need to round the decimal to a reasonable number of decimal places before converting it to a percentage. The level of precision needed depends on the context of the problem.
Q4: Why is understanding this conversion important?
A4: Understanding this conversion is crucial for various real-world applications, from financial calculations to scientific analysis. It's a foundational skill that improves numerical literacy and problem-solving abilities.
Q5: How can I practice more fraction-to-percentage conversions?
A5: Practice is key! Try converting different fractions to percentages. Start with simple fractions and gradually move towards more complex ones. You can find numerous online resources and exercises to help you practice.
Conclusion: Mastering the Conversion of 5/8 to a Percentage
Converting 5/8 to a percentage – resulting in 62.5% – is a fundamental skill with far-reaching applications. This article provided a comprehensive explanation of the process, delved into the mathematical rationale behind it, and highlighted its real-world relevance. By mastering this skill, you improve your mathematical understanding, enhance your problem-solving abilities, and gain a valuable tool applicable across various disciplines and everyday situations. Remember, the key is to understand the relationship between fractions, decimals, and percentages – a relationship that underpins much of our numerical world. Consistent practice will solidify your understanding and make this conversion process second nature.
Latest Posts
Latest Posts
-
You Should Cut Metal Banding
Sep 10, 2025
-
Convert 4 1 Kilometers To Centimeters
Sep 10, 2025
-
Dietary Recalls Include Information About
Sep 10, 2025
-
Before Heavily Soiled Condiment Pans
Sep 10, 2025
-
What Is 2 Of 180
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 5 8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.