5 X 2 2 125
cibeltiagestion
Sep 10, 2025 · 6 min read
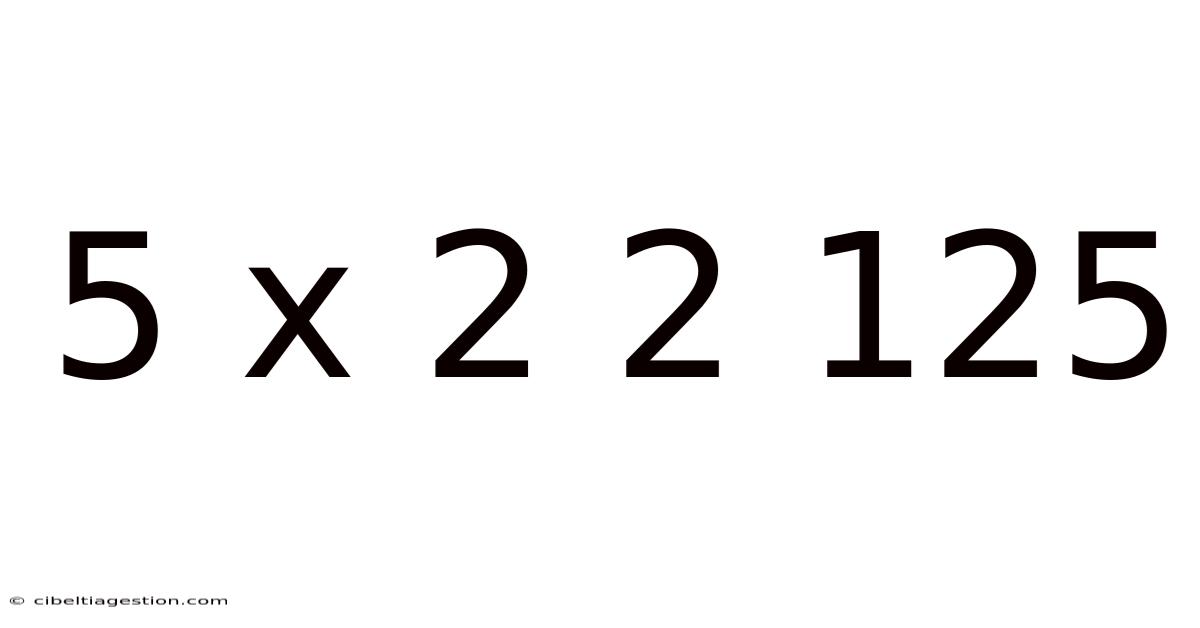
Table of Contents
Decoding the Enigma: Exploring the Mathematical Puzzle of 5 x 2 2 125
The seemingly simple sequence "5 x 2 2 125" might initially appear as a random string of numbers. However, a closer look reveals a fascinating mathematical puzzle that blends basic arithmetic with a touch of lateral thinking. This article delves into the intricacies of this sequence, exploring various interpretations, potential solutions, and the underlying mathematical principles at play. We’ll unravel the mystery step by step, uncovering the logic behind this intriguing numerical riddle. Understanding this puzzle helps build critical thinking skills and reinforces fundamental mathematical concepts.
Understanding the Problem: Breaking Down the Sequence
At first glance, "5 x 2 2 125" seems ambiguous. The lack of clear operators between the numbers leaves room for multiple interpretations. Is it a simple multiplication problem? A sequence following a specific pattern? Or something more complex requiring unconventional mathematical operations? The challenge lies in deciphering the intended relationship between the numbers and identifying the hidden logic. The key to solving this puzzle lies in exploring different mathematical perspectives and considering less obvious possibilities.
Potential Interpretations and Solutions
Let's explore some possible ways to interpret and solve this mathematical puzzle:
1. The Straightforward Approach (and its limitations):
The most immediate interpretation is to treat the sequence as a simple multiplication problem: 5 multiplied by 2, then 2 again, and finally 125. This would yield: 5 x 2 = 10; 10 x 2 = 20; 20 x 125 = 2500. However, this approach lacks elegance and doesn't feel like a satisfying solution. It doesn't leverage the inherent "enigmatic" nature of the problem statement.
2. Exploring Base-10 Number Systems:
A more sophisticated approach involves considering the positional values of the numbers within the sequence. Could the sequence represent a number in a different base system? While unlikely to yield a single definitive answer, exploring this route enhances our understanding of number systems. For instance, we could analyze if the sequence could represent a number expressed in base-2 (binary), base-8 (octal), base-16 (hexadecimal), or even a custom base system. However, directly interpreting "5 x 2 2 125" as a number in a different base requires more context or additional information.
3. Considering Order of Operations (PEMDAS/BODMAS):
The principles of order of operations (often remembered by the acronyms PEMDAS or BODMAS – Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) are crucial in evaluating mathematical expressions. If we insert operators into the sequence, considering PEMDAS, we can derive various results. For example:
- (5 x 2) + 2 + 125 = 139 (This uses standard multiplication and addition)
- 5 x (2 + 2) + 125 = 145 (This prioritizes the addition within parentheses)
- 5 x (2 x 2) + 125 = 145 (Prioritizes the multiplication before addition)
- 5 x 2 x 2 + 125 = 145 (A simpler version of the above)
4. Unconventional Mathematical Operations:
The puzzle could also involve unconventional operations not explicitly stated. We might explore possibilities involving:
- Factorials (!): The factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. This could be relevant if we find factorial operations within the sequence.
- Modulus (%): The modulus operator gives the remainder after division. This could be used to introduce a pattern if we assume the number 125 acts as a divisor or modulo.
- Exponents: Raising a number to a power (e.g., 5²) can dramatically alter the outcome.
5. Geometric Progression/Series:
The sequence could also represent a hidden geometric progression or series. A geometric progression is a sequence where each term is found by multiplying the previous term by a constant. Looking for this underlying pattern may reveal a consistent ratio between numbers in the sequence. However, this doesn't immediately apply given the nature of the numbers provided without additional contextual information.
The Importance of Context and Further Exploration
Solving the "5 x 2 2 125" puzzle highlights the importance of considering context. Without additional information or clear instructions on the intended mathematical operations, multiple solutions are possible. The puzzle serves as an excellent exercise in critical thinking and problem-solving, pushing us to think outside the box and explore different mathematical approaches.
If this sequence were part of a larger problem, such as a coding challenge or a mathematical game, additional clues would likely be provided. These clues might specify the type of operations allowed or the intended result, leading to a more definitive solution.
The ambiguity of the puzzle also forces us to consider potential errors or omissions in the original statement. It's essential to verify the accuracy of the sequence and explore alternative interpretations, acknowledging the limitations of the information provided.
Expanding Our Mathematical Horizons
Working through this seemingly simple puzzle expands our mathematical horizons in several key ways:
- Reinforces fundamental operations: The puzzle touches upon basic arithmetic operations like multiplication and addition, solidifying our understanding of their application.
- Introduces different number systems: Exploring the possibility of different base systems encourages us to broaden our perspectives on number representation.
- Highlights the importance of order of operations: The varying results obtained by changing the order of operations emphasize the significance of PEMDAS/BODMAS in mathematical calculations.
- Stimulates creative problem-solving: It challenges us to think beyond straightforward solutions and explore less obvious mathematical concepts, thereby enhancing our creative problem-solving skills.
Frequently Asked Questions (FAQs)
Q: Is there a single definitive answer to this puzzle?
A: Without additional context or constraints, there isn't a single definitive answer. Multiple interpretations and solutions are valid depending on the assumed mathematical operations.
Q: Could this puzzle be part of a larger mathematical problem?
A: Absolutely. This sequence could be a small component of a more complex problem, where additional information or constraints would narrow down the possible solutions.
Q: What are the key skills developed by solving this type of puzzle?
A: Solving this type of puzzle enhances critical thinking, problem-solving, and the ability to explore various mathematical approaches. It also reinforces fundamental mathematical concepts.
Q: Why is it important to consider different number systems?
A: Exploring different number systems allows for a more comprehensive understanding of number representation and opens up possibilities for solutions that might not be apparent within the standard base-10 system.
Conclusion: Embracing Mathematical Curiosity
The "5 x 2 2 125" puzzle, while seemingly simple, provides a rich opportunity to explore the diverse facets of mathematics. Its ambiguous nature encourages lateral thinking and the application of various mathematical concepts. By analyzing this puzzle, we gain a deeper understanding of arithmetic operations, number systems, and the importance of context in problem-solving. Ultimately, it reminds us to embrace mathematical curiosity and to explore different avenues when tackling seemingly simple yet surprisingly complex problems. The journey of uncovering the possible solutions is as valuable as finding a single "correct" answer, as it enhances our overall mathematical reasoning skills and broadens our understanding of the world of numbers. Therefore, continue to explore, experiment, and enjoy the challenges that mathematics presents!
Latest Posts
Latest Posts
-
According To Virtue Ethics Emotions
Sep 10, 2025
-
Dna Replication In Chronological Order
Sep 10, 2025
-
What Is 10 Of 1200 00
Sep 10, 2025
-
What Is A Contour Interval
Sep 10, 2025
-
Is Salad Biotic Or Abiotic
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 5 X 2 2 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.