60 Is 1 10 Of
cibeltiagestion
Sep 12, 2025 · 5 min read
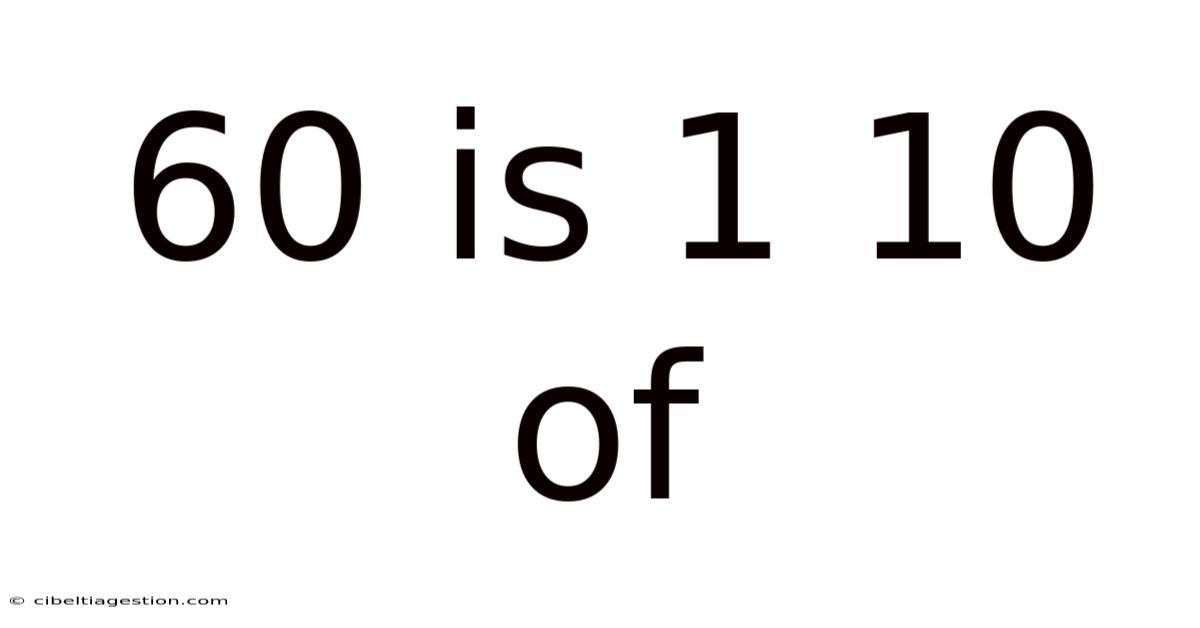
Table of Contents
60 is 1/10 of: Understanding Percentages and Proportions
This article explores the concept of percentages and proportions, using the example "60 is 1/10 of what number?" We'll delve into the mathematical methods for solving this type of problem, explain the underlying principles, and offer practical applications to solidify your understanding. This will cover various approaches, from basic arithmetic to more advanced proportional reasoning, ensuring a comprehensive grasp of this fundamental mathematical concept.
Understanding the Problem: 60 is 1/10 of What?
The statement "60 is 1/10 of what number?" essentially asks us to find the whole amount when a fraction (1/10) of it is known to be 60. This is a classic problem involving proportions, and it highlights the crucial relationship between parts and wholes. Understanding this relationship is key to solving a wide range of problems in mathematics, science, and everyday life.
Method 1: Using Basic Arithmetic (Multiplication)
The simplest way to approach this problem is to use basic multiplication. If 60 represents one-tenth (1/10) of a larger number, we can find the whole number by multiplying 60 by 10.
- Calculation: 60 x 10 = 600
Therefore, 60 is 1/10 of 600.
This method directly addresses the problem's core: finding the whole when a fraction of it is given. It's a straightforward and efficient approach for simple problems involving readily identifiable fractions.
Method 2: Setting up a Proportion
A more formal and versatile method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. In this case, we can set up a proportion as follows:
- 1/10 = 60/x
Where:
- 1/10 represents the given fraction.
- 60 represents the known part.
- x represents the unknown whole we are trying to find.
To solve this proportion, we can use cross-multiplication:
- 1 * x = 10 * 60
- x = 600
This method reinforces the concept of equivalent ratios and provides a structured approach to solving similar problems, even when dealing with more complex fractions. It is particularly useful when the fraction isn't as easily recognizable as 1/10.
Method 3: Using Percentage Equivalence
Since 1/10 is equivalent to 10%, the problem can be rephrased as: "60 is 10% of what number?" This approach leverages the relationship between fractions and percentages, opening up another avenue for solving the problem.
To solve this using percentages:
- We know that 10% of a number is 60.
- To find 100% (the whole number), we can use the following equation:
(10/100) * x = 60
- Simplifying, we get:
0.1 * x = 60
- Dividing both sides by 0.1:
x = 60 / 0.1 = 600
Again, we arrive at the answer: 60 is 10% (or 1/10) of 600. This method highlights the versatility of percentage calculations and their direct connection to fractions.
Extending the Concept: Proportional Reasoning
The problem "60 is 1/10 of what number?" is a fundamental illustration of proportional reasoning. Proportional reasoning is a crucial cognitive skill involving the understanding of relationships between quantities. It’s essential for problem-solving across numerous disciplines.
Here’s how proportional reasoning applies:
- Understanding Ratios: The problem highlights the ratio between a part (60) and the whole (unknown). The ratio is given as 1:10 (or 1/10).
- Scaling Ratios: We use the known ratio to scale up to find the whole. Since 60 is one-tenth, we multiply by 10 to find the full amount.
- Applications: Proportional reasoning extends far beyond simple math problems. It’s used in cooking (scaling recipes), construction (calculating materials), map reading (interpreting scales), and countless other real-world applications.
Mastering proportional reasoning improves your analytical skills and problem-solving capabilities in various contexts.
Real-World Applications
Understanding proportions and percentages is vital in many real-world scenarios:
- Finance: Calculating interest, discounts, taxes, and investment returns all rely heavily on percentages and proportional reasoning.
- Science: Proportions are fundamental to chemistry (concentration calculations), physics (ratios of forces), and biology (population growth).
- Cooking: Scaling recipes up or down requires understanding proportions to maintain the correct ratios of ingredients.
- Shopping: Calculating discounts, comparing prices, and understanding sales taxes all utilize percentage calculations.
- Data Analysis: Interpreting statistics and data often involves understanding proportions and percentages to draw meaningful conclusions.
Frequently Asked Questions (FAQ)
Q1: What if the fraction was different? For example, "60 is 2/5 of what number?"
A1: The same principles apply. You can use any of the methods described above. For the example given, you would set up a proportion: 2/5 = 60/x. Cross-multiplying would give you 2x = 300, resulting in x = 150. Alternatively, you could find what 1/5 is (60/2 = 30) and then multiply by 5 to find the whole (30 * 5 = 150).
Q2: How can I improve my understanding of percentages and proportions?
A2: Practice is key. Solve numerous problems with varying fractions and percentages. Start with simple problems and gradually work towards more complex ones. Utilize online resources, textbooks, and practice exercises to enhance your understanding and problem-solving skills.
Q3: Are there other ways to solve this type of problem?
A3: Yes, you could also utilize algebraic equations. For example, you could represent the unknown number as 'x' and write the equation: (1/10)x = 60. Solving for 'x' would again yield the answer 600.
Q4: What if the number isn't a whole number?
A4: The methods remain the same. The calculations might involve decimals, but the underlying principles of proportion and percentage remain consistent. For example, if the problem were "15 is 1/10 of what number?" You'd still multiply 15 by 10, resulting in 150.
Conclusion: Mastering Proportions and Percentages
The problem "60 is 1/10 of what number?" serves as a springboard for understanding the broader concepts of proportions and percentages. Mastering these concepts isn't just about solving mathematical problems; it's about developing critical thinking skills applicable to numerous real-world scenarios. By applying the methods described – basic arithmetic, proportions, and percentage equivalence – and practicing regularly, you can build a strong foundation in proportional reasoning and confidently tackle similar problems in various contexts. Remember that the core principle lies in understanding the relationship between parts and the whole, and applying that understanding to different mathematical expressions.
Latest Posts
Latest Posts
-
Number Of Protons In Phosphorus
Sep 12, 2025
-
Markets Are Classified As Either
Sep 12, 2025
-
10 Examples Of Reciprocating Motion
Sep 12, 2025
-
Mg Clo4 2 Molar Mass
Sep 12, 2025
-
Is No2 Molecular Or Ionic
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 60 Is 1 10 Of . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.