7 1/3 X 2 2/11
cibeltiagestion
Sep 06, 2025 · 5 min read
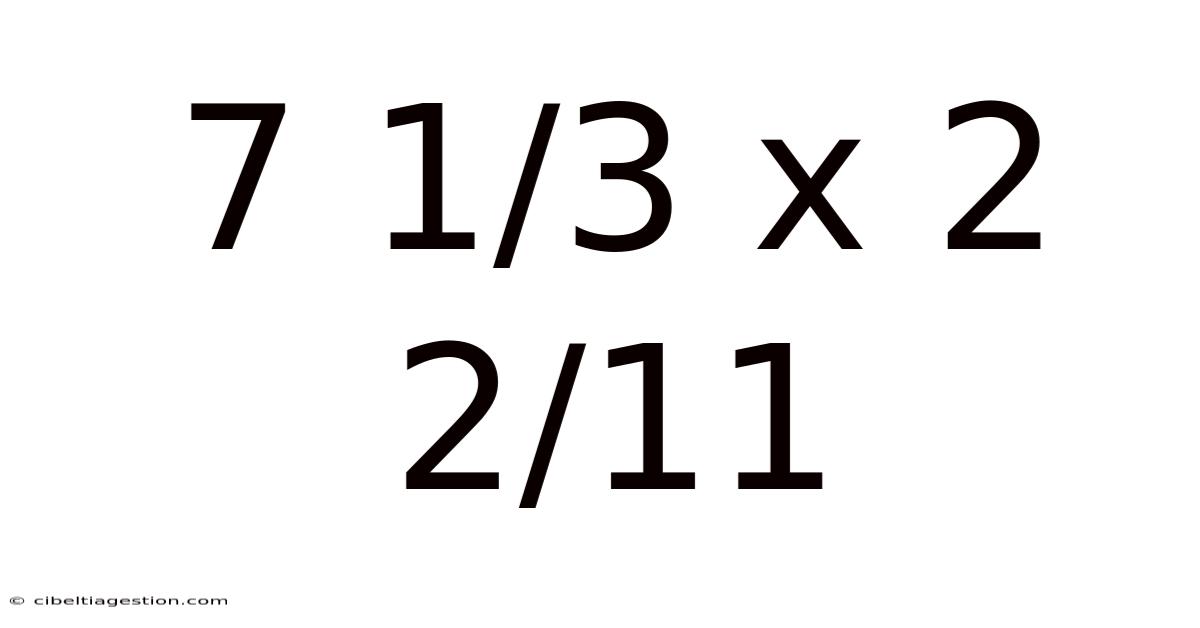
Table of Contents
Decoding the Mystery: A Deep Dive into 7 1/3 x 2 2/11
This article will explore the seemingly simple, yet surprisingly nuanced, mathematical problem of multiplying mixed numbers: 7 1/3 x 2 2/11. We'll break down the process step-by-step, examine the underlying principles, and delve into the reasons behind each calculation. Understanding this seemingly basic problem lays the foundation for more complex mathematical concepts, reinforcing crucial skills in fraction manipulation and multiplication. This comprehensive guide will equip you with the confidence to tackle similar problems with ease.
Understanding Mixed Numbers
Before diving into the multiplication, let's solidify our understanding of mixed numbers. A mixed number combines a whole number and a fraction. For example, 7 1/3 represents 7 whole units plus 1/3 of another unit. Similarly, 2 2/11 represents 2 whole units and 2/11 of another. To perform multiplication effectively, we need to convert these mixed numbers into a more manageable form: improper fractions.
Converting Mixed Numbers to Improper Fractions
Converting a mixed number to an improper fraction involves expressing the entire quantity as a fraction where the numerator (top number) is larger than the denominator (bottom number). Here's how we do it:
- Multiply the whole number by the denominator: For 7 1/3, we multiply 7 by 3, resulting in 21.
- Add the numerator: We then add the numerator (1) to the result from step 1: 21 + 1 = 22.
- Keep the same denominator: The denominator remains the same (3).
- Form the improper fraction: The improper fraction for 7 1/3 is therefore 22/3.
Let's apply the same steps to 2 2/11:
- Multiply the whole number by the denominator: 2 x 11 = 22.
- Add the numerator: 22 + 2 = 24.
- Keep the same denominator: The denominator remains 11.
- Form the improper fraction: The improper fraction for 2 2/11 is 24/11.
Multiplying Improper Fractions
Now that we've converted our mixed numbers into improper fractions, we can proceed with the multiplication: 22/3 x 24/11. Multiplying fractions is straightforward:
- Multiply the numerators: 22 x 24 = 528.
- Multiply the denominators: 3 x 11 = 33.
- Form the resulting fraction: This gives us the improper fraction 528/33.
Simplifying the Result
The fraction 528/33 is an improper fraction, and it can be simplified. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. In this case, the GCD of 528 and 33 is 33.
Dividing both the numerator and denominator by 33:
528 ÷ 33 = 16 33 ÷ 33 = 1
This simplifies our fraction to 16/1, which is simply 16.
Therefore, 7 1/3 x 2 2/11 = 16
A Deeper Look: The Commutative Property and Simplification Strategies
The order in which we multiply fractions doesn't affect the outcome, thanks to the commutative property of multiplication. This means that a x b = b x a. While we multiplied 22/3 by 24/11 directly, we could have simplified before multiplying to make the calculation easier. Notice that 22 and 11 share a common factor of 11:
22/11 simplifies to 2/1.
Our multiplication would then become:
(2/1) x (24/3)
Notice that 24 and 3 share a common factor of 3:
24/3 simplifies to 8/1
Our simplified multiplication becomes:
(2/1) x (8/1) = 16/1 = 16
This illustrates how simplifying before multiplying can significantly reduce the complexity of calculations, particularly when dealing with larger numbers.
Real-World Applications
Understanding the multiplication of mixed numbers is crucial in various real-world situations:
- Cooking and Baking: Recipes often require scaling up or down, involving the multiplication of fractional quantities of ingredients.
- Construction and Engineering: Precise measurements and calculations using fractions are essential for accurate building and design.
- Finance and Budgeting: Calculating percentages, interest rates, and proportions frequently involves fraction manipulation.
- Science and Research: Scientific experiments and data analysis frequently require calculations involving fractions and mixed numbers.
Frequently Asked Questions (FAQ)
Q: What if I made a mistake in converting the mixed numbers to improper fractions?
A: An error in the conversion will inevitably lead to an incorrect final answer. Double-check your conversion steps carefully to ensure accuracy.
Q: Can I use a calculator to solve this problem?
A: Yes, many calculators can handle mixed number multiplication. However, understanding the underlying process is essential for building mathematical fluency and problem-solving skills.
Q: Are there other methods to solve this problem?
A: While the improper fraction method is generally preferred for its efficiency, you could also convert the mixed numbers to decimals and then multiply. However, this might introduce rounding errors and is less precise than working with fractions.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes the results easier to understand and interpret. It also reduces the risk of errors in subsequent calculations.
Conclusion
Multiplying mixed numbers, like 7 1/3 x 2 2/11, may seem daunting at first, but by breaking down the process into manageable steps – converting to improper fractions, performing the multiplication, and simplifying the result – the task becomes much simpler. Understanding the underlying mathematical principles, such as the commutative property and the importance of simplifying fractions, enhances not only your ability to solve this specific problem but also strengthens your overall mathematical foundation. This deep dive has equipped you with the tools and understanding to confidently approach similar problems, reinforcing essential skills applicable across various fields and everyday situations. Remember, practice is key; the more you work with fractions and mixed numbers, the more comfortable and proficient you’ll become.
Latest Posts
Latest Posts
-
What Is A Sancho Food
Sep 06, 2025
-
What Is A Dialectical Shape
Sep 06, 2025
-
Where Can Utensils Be Stored
Sep 06, 2025
-
What Is 20 Of 780
Sep 06, 2025
-
Which Table Represents A Function
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 7 1/3 X 2 2/11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.