7 X 3 9x 10
cibeltiagestion
Sep 08, 2025 · 5 min read
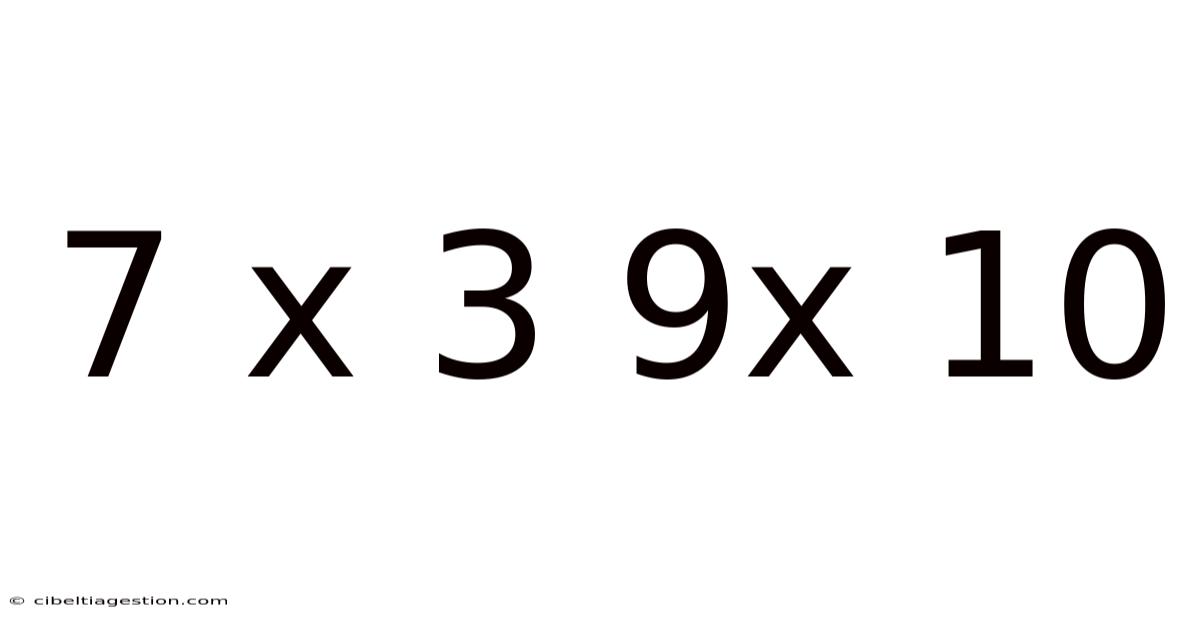
Table of Contents
Decoding the Mystery: Exploring the Mathematical Relationship Between 7 x 3 and 9 x 10
This article delves into the seemingly disparate mathematical expressions, 7 x 3 and 9 x 10. While at first glance these appear to be unrelated simple multiplication problems, a deeper exploration reveals interesting connections and opportunities to learn about fundamental mathematical concepts, including prime numbers, composite numbers, factorization, and the distributive property. We'll move beyond simply calculating the answers and uncover the underlying mathematical structures that govern these operations.
Introduction: More Than Just Multiplication
The seemingly simple equations, 7 x 3 and 9 x 10, offer a rich landscape for mathematical exploration. The immediate results, 21 and 90 respectively, are just the starting point. We'll investigate their prime factorizations, common factors, and how they relate to broader mathematical principles. This exploration will be beneficial for students at various levels, from elementary school to those seeking a deeper understanding of number theory.
Understanding the Basics: Multiplication and Factors
Before we delve into the deeper connections, let's refresh our understanding of fundamental concepts. Multiplication is a fundamental arithmetic operation representing repeated addition. For example, 7 x 3 is the same as 7 + 7 + 7, resulting in 21. A factor is a number that divides another number without leaving a remainder. For instance, the factors of 21 are 1, 3, 7, and 21. Similarly, the factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90.
Prime Factorization: Unveiling the Building Blocks
Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Let's find the prime factorization of both 21 and 90:
-
21: The prime factorization of 21 is 3 x 7. Both 3 and 7 are prime numbers.
-
90: The prime factorization of 90 is 2 x 3 x 3 x 5, which can also be written as 2 x 3² x 5. Here, 2, 3, and 5 are prime numbers.
This reveals a key difference: 21 is composed of two distinct prime factors, while 90 is composed of three distinct prime factors, with one repeated. This simple observation opens doors to understanding the unique properties of each number.
Exploring Common Factors and Greatest Common Divisor (GCD)
While 21 and 90 have distinct prime factorizations, they also share a common factor: 3. The Greatest Common Divisor (GCD) is the largest number that divides both numbers without leaving a remainder. In this case, the GCD of 21 and 90 is 3. This shared factor highlights a subtle connection between these seemingly disparate numbers. Understanding GCD is crucial in various mathematical applications, including simplifying fractions and solving equations.
The Distributive Property: Connecting the Expressions
The distributive property of multiplication over addition states that a(b + c) = ab + ac. This property allows us to manipulate and connect different mathematical expressions. While not directly applicable in the simplest form of 7 x 3 and 9 x 10, we can explore its application with related expressions. Consider the following:
Let's say we want to express 90 as a sum of multiples of 21. We can rewrite 90 as 21 + 21 + 21 + 21 + 6. This can be expressed as 4(21) + 6. This demonstrates a connection between 21 and 90 through the distributive property, though it's a more complex application than a direct relationship.
Beyond Simple Multiplication: Expanding the Scope
The initial problem extends beyond simple multiplication. We've explored prime factorization, GCD, and the distributive property, demonstrating that even basic arithmetic operations hold a wealth of underlying mathematical richness. The seemingly simple numbers 21 and 90 provide a platform to discuss concepts essential to more advanced mathematics.
Applications in Real-World Scenarios
The concepts explored here—multiplication, prime factorization, and GCD—are not confined to theoretical mathematics. They find practical applications in various fields:
-
Computer Science: Prime factorization is crucial in cryptography, particularly in RSA encryption, which secures online transactions and data.
-
Engineering: Understanding factors and divisors is fundamental in design and construction, ensuring structural integrity and efficiency.
-
Everyday Life: We unconsciously use these concepts in daily tasks like dividing items equally or determining the optimal arrangement of objects.
Further Exploration: Expanding Mathematical Horizons
This exploration of 7 x 3 and 9 x 10 has just scratched the surface of the mathematical landscape. Further investigations can delve into:
-
Least Common Multiple (LCM): The smallest number that is a multiple of both 21 and 90.
-
Modular Arithmetic: Exploring the remainders when 21 and 90 are divided by different numbers.
-
Number Theory: Investigating advanced concepts like divisibility rules and Fermat's Little Theorem.
Frequently Asked Questions (FAQ)
Q: What is the significance of prime factorization?
A: Prime factorization is fundamental in number theory and cryptography. It allows us to understand the building blocks of a number and reveals its unique properties.
Q: How is the GCD useful?
A: The GCD is used to simplify fractions, solve equations, and is important in various areas of mathematics and computer science.
Q: Can any two numbers always be expressed using the distributive property?
A: Not directly in all cases. The distributive property works most effectively when we can find a common factor between the numbers.
Q: Are there any other interesting relationships between 21 and 90?
A: While we've explored some key relationships, further analysis could uncover additional mathematical connections, depending on the specific mathematical concepts being investigated.
Conclusion: The Unfolding Beauty of Numbers
The seemingly simple multiplication problems, 7 x 3 and 9 x 10, lead to a rich exploration of fundamental mathematical concepts. By moving beyond simply calculating the answers, we uncovered deeper connections and applications. This journey highlights the beauty and complexity inherent within even the simplest numbers, encouraging us to explore the mathematical world with curiosity and a deeper understanding. This exploration emphasizes that mathematics is not just about memorizing facts but about understanding underlying principles and their interconnections. The seemingly simple numbers 21 and 90 serve as excellent examples of the depth and complexity that lie within the field of mathematics, waiting to be explored. The more we investigate, the more we discover the fascinating relationships that govern the world of numbers.
Latest Posts
Latest Posts
-
Convert 17 C To F
Sep 09, 2025
-
Is Photosynthesis Endergonic Or Exergonic
Sep 09, 2025
-
Convert 190 Celsius To Fahrenheit
Sep 09, 2025
-
6 Out Of 7 Percentage
Sep 09, 2025
-
Bucketing Getting Ready To Write
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 7 X 3 9x 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.