7x18 45 Divided By 3x2
cibeltiagestion
Sep 06, 2025 · 5 min read
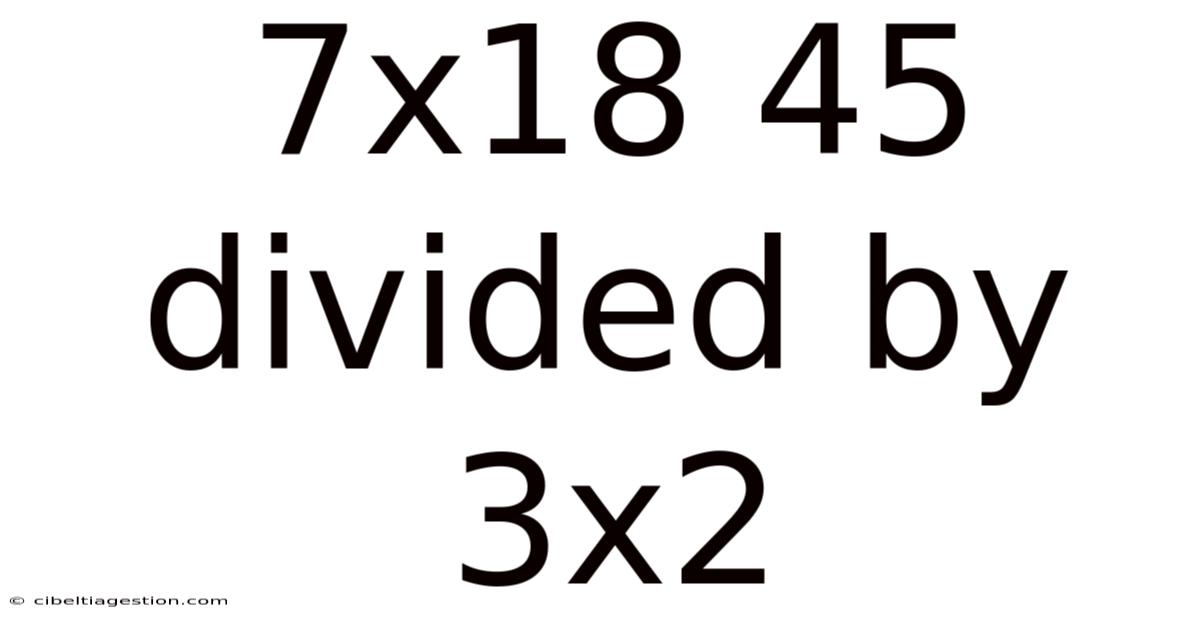
Table of Contents
Deconstructing the Mathematical Expression: 7x18 + 45 ÷ 3x2
This article delves into the seemingly simple mathematical expression "7 x 18 + 45 ÷ 3 x 2," explaining not only the solution but also the underlying principles of order of operations (often remembered by the acronym PEMDAS/BODMAS) and why understanding these principles is crucial for accurate calculations. We'll break down the problem step-by-step, clarifying potential areas of confusion and highlighting the importance of precise mathematical notation. This exploration will be beneficial for students learning basic arithmetic, as well as anyone looking to refresh their understanding of fundamental mathematical concepts.
Understanding Order of Operations (PEMDAS/BODMAS)
Before we tackle the expression, it’s vital to understand the order of operations. This set of rules dictates the sequence in which we perform calculations to ensure a consistent and unambiguous result. The acronyms PEMDAS and BODMAS both represent the same order:
- Parentheses/Brackets: Calculations within parentheses or brackets are always performed first.
- Exponents/Orders: Exponents (powers) and roots are evaluated next.
- Multiplication and Division: These operations have equal precedence and are performed from left to right.
- Addition and Subtraction: These operations also have equal precedence and are performed from left to right.
Remember the crucial point: Multiplication and division are done before addition and subtraction, but they are performed in order from left to right, as are addition and subtraction.
Step-by-Step Solution of 7 x 18 + 45 ÷ 3 x 2
Now let's apply PEMDAS/BODMAS to solve our expression: 7 x 18 + 45 ÷ 3 x 2
Step 1: Multiplication and Division (from left to right)
The expression contains multiplication and division. Following the order of operations, we perform these operations from left to right:
- First, we calculate 7 x 18 = 126.
- Next, we calculate 45 ÷ 3 = 15.
- Our expression now simplifies to: 126 + 15 x 2
Then, we perform the remaining multiplication:
15 x 2 = 30
The expression further simplifies to: 126 + 30
Step 2: Addition
Finally, we perform the addition:
- 126 + 30 = 156
Therefore, the solution to the expression 7 x 18 + 45 ÷ 3 x 2 is 156.
The Importance of Precise Notation
The seemingly simple nature of this problem highlights the importance of clear mathematical notation. Ambiguity in how the expression is written can lead to different interpretations and incorrect answers. For example, if the expression were written differently, like (7 x 18) + (45 ÷ 3) x 2, the parentheses would force us to calculate the expressions within the parentheses first, potentially changing the final result. Similarly, the absence of parentheses could also lead to different interpretations.
Consider the impact of misplaced parentheses:
- (7 x 18 + 45) ÷ (3 x 2): This would require us to perform the operations within the parentheses first, leading to a different outcome.
Always ensure that mathematical expressions are written clearly to prevent misunderstandings and calculation errors. Proper use of parentheses is essential for removing ambiguity and guaranteeing the correct solution.
Illustrative Examples: Similar Problems and Their Solutions
Let's explore some similar examples to further reinforce the concept of order of operations:
Example 1: 20 + 5 x 4 – 10 ÷ 2
- Multiplication and Division (left to right): 5 x 4 = 20; 10 ÷ 2 = 5
- Expression becomes: 20 + 20 – 5
- Addition and Subtraction (left to right): 20 + 20 = 40; 40 – 5 = 35 Solution: 35
Example 2: (12 ÷ 4) x 3 + 6 – 2
- Parentheses: 12 ÷ 4 = 3
- Expression becomes: 3 x 3 + 6 – 2
- Multiplication: 3 x 3 = 9
- Expression becomes: 9 + 6 – 2
- Addition and Subtraction (left to right): 9 + 6 = 15; 15 – 2 = 13 Solution: 13
Example 3: 3² + 4 x 5 – 15 ÷ 3
- Exponents: 3² = 9
- Expression becomes: 9 + 4 x 5 – 15 ÷ 3
- Multiplication and Division (left to right): 4 x 5 = 20; 15 ÷ 3 = 5
- Expression becomes: 9 + 20 – 5
- Addition and Subtraction (left to right): 9 + 20 = 29; 29 – 5 = 24 Solution: 24
These examples further demonstrate the importance of diligently applying the rules of PEMDAS/BODMAS to achieve accurate results.
Beyond Basic Arithmetic: Implications in Advanced Mathematics
While this article focuses on a simple arithmetic problem, the principles of order of operations extend to much more complex mathematical concepts. In algebra, calculus, and beyond, adhering to the correct order of operations is crucial for solving equations and performing calculations accurately. Failure to do so will lead to incorrect results and a flawed understanding of mathematical relationships.
Understanding the precedence of operations isn't just about getting the right answer; it’s about understanding the language of mathematics. It’s a fundamental building block for more advanced studies.
Frequently Asked Questions (FAQ)
Q: What if I perform the operations in a different order?
A: If you deviate from the order of operations (PEMDAS/BODMAS), you will almost certainly arrive at an incorrect answer. The order of operations ensures consistency and avoids ambiguity in mathematical calculations.
Q: Why is the order of operations important?
A: The order of operations is essential for consistency and unambiguous interpretation of mathematical expressions. Without a standard order, different people could obtain different results from the same expression.
Q: Are there any exceptions to the order of operations?
A: Generally, no. Parentheses are used to override the standard order, but they don't create exceptions. They provide a way to explicitly define the order of calculation.
Q: How can I improve my understanding of order of operations?
A: Practice is key. Work through numerous examples, gradually increasing the complexity. Utilize online resources and educational materials for further learning and reinforcement.
Conclusion
Solving the expression 7 x 18 + 45 ÷ 3 x 2 requires a firm grasp of the order of operations (PEMDAS/BODMAS). By following these rules systematically, we arrive at the correct solution: 156. This seemingly simple problem serves as a powerful illustration of why understanding these fundamental principles is essential not only for basic arithmetic but also for tackling more advanced mathematical concepts. Mastering order of operations is a critical step in building a solid foundation in mathematics and ensuring accurate calculations in any field that utilizes numbers. Consistent practice and a clear understanding of the rules are the keys to success. Remember to always strive for clear and unambiguous notation to prevent misinterpretations and errors in your calculations.
Latest Posts
Latest Posts
-
Abrasive Cleaners Cause Friction Which
Sep 06, 2025
-
How Many Electrons In Naf
Sep 06, 2025
-
If You Find Yourself Hydroplaning
Sep 06, 2025
-
Pre Lab Study Questions 18
Sep 06, 2025
-
He Eats Apples In Spanish
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 7x18 45 Divided By 3x2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.