8x 2 10 6x 2
cibeltiagestion
Sep 12, 2025 · 5 min read
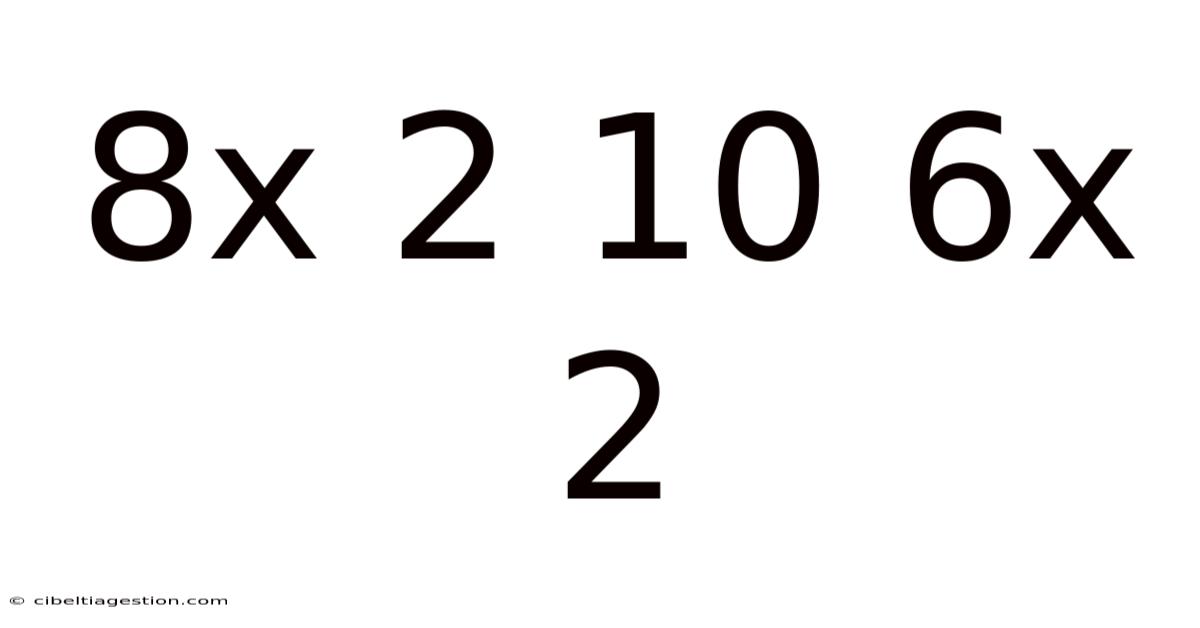
Table of Contents
Decoding the Enigma: A Deep Dive into 8x 2, 10, 6x 2 and the Underlying Mathematical Principles
This article explores the seemingly simple yet surprisingly rich mathematical concepts hidden within the sequence "8x 2, 10, 6x 2". We'll delve into the potential interpretations, unravel the underlying principles, and examine the various mathematical operations that could be at play. This isn't just about finding a single answer; it's about understanding the process of mathematical problem-solving and appreciating the beauty of multiple approaches.
Introduction: Unveiling the Mystery
At first glance, "8x 2, 10, 6x 2" appears to be a random collection of numbers and symbols. However, a closer look reveals a potential pattern involving multiplication and addition, or perhaps a more complex sequence based on hidden relationships. The key to unlocking this enigma lies in understanding the different ways we can interpret mathematical expressions and the possibilities of hidden patterns. We'll explore different perspectives to uncover the potential logic behind this numerical sequence.
Potential Interpretations and Mathematical Operations
The sequence "8x 2, 10, 6x 2" suggests several potential interpretations:
-
A Simple Arithmetic Sequence with Multiplication and Addition: One straightforward interpretation involves performing the multiplications first and then considering the relationship between the resulting numbers. This approach leads to:
- 8 x 2 = 16
- 6 x 2 = 12
This results in the sequence 16, 10, 12. While not immediately obvious, we can analyze the differences between consecutive terms:
- 10 - 16 = -6
- 12 - 10 = 2
This doesn't reveal a consistent pattern in simple differences. However, we can investigate further by exploring other mathematical operations or looking for patterns in other properties of these numbers.
-
A More Complex Pattern involving Sequences and Series: We might consider this as part of a larger, more complex sequence. Perhaps the numbers are part of a Fibonacci-like sequence with a twist, or they represent terms in a series defined by a recursive formula. For example, there might be a pattern in the prime factorization of each number or in their digital roots. Let's analyze the prime factorizations:
- 16 = 2<sup>4</sup>
- 10 = 2 x 5
- 12 = 2<sup>2</sup> x 3
Again, no readily apparent pattern is evident from the prime factorization. This suggests we might need to investigate alternative methods.
-
Considering the "x" as an Unknown Variable: Another approach is to treat the "x" as a variable and attempt to solve for it in some equation. This approach requires more information or context. For instance, if we assume that the numbers form an arithmetic progression where 'x' is a common difference, or if they represent points in a coordinate system, we would need additional equations to solve for 'x' definitively.
-
Exploring Base Number Systems: Could the numbers be represented in a different base number system, other than the standard base-10 system? Changing bases could reveal a hidden pattern. However, without further information or context, this avenue is purely speculative.
Expanding the Possibilities: Introducing Context
The lack of context surrounding the sequence "8x 2, 10, 6x 2" severely limits our ability to arrive at a definitive solution. To meaningfully analyze this sequence, we need more information. For example:
- Is this part of a larger sequence? If there are more numbers before or after this snippet, we can analyze the overall pattern more effectively. Extending the sequence is essential for discovering hidden trends.
- What is the context or application? Is this a puzzle, a code, or part of a mathematical problem? Understanding its origin could provide valuable clues about the underlying principles at play. The context dictates the appropriate methods of analysis.
- Are there any additional constraints or rules? Are the operations restricted to multiplication and addition? Are specific mathematical properties of the numbers relevant? These limitations significantly affect the range of potential solutions.
A Deeper Dive into Mathematical Problem-Solving
The analysis of "8x 2, 10, 6x 2" highlights the crucial aspects of mathematical problem-solving:
- Systematic Approach: We approached the problem systematically, starting with simple interpretations and moving towards more complex ones. This involves testing various mathematical operations and exploring different perspectives.
- Pattern Recognition: The ability to recognize patterns is crucial in solving mathematical problems. We looked for patterns in differences, prime factorization, and other properties of the numbers.
- The Importance of Context: Context is essential in mathematical problem-solving. The lack of context significantly restricts our ability to find a definitive solution. Additional information greatly enhances our ability to formulate hypotheses and arrive at sound conclusions.
- Embrace Multiple Solutions: There might be multiple valid interpretations of the sequence, depending on the context and assumptions. The challenge lies in identifying the most likely or most relevant solution based on available information.
Frequently Asked Questions (FAQ)
-
Is there a single correct answer? Without additional context, there is no single definitively correct answer. The goal is to explore potential interpretations and understand the underlying mathematical principles.
-
What if the "x" represents multiplication? If "x" represents multiplication, we've already explored this interpretation and found no clear pattern.
-
Could this be a coding puzzle? It's possible. In coding, this might represent a sequence of operations or data points.
-
What other mathematical concepts could be relevant? Modular arithmetic, number theory, and abstract algebra could be explored if more context is provided.
Conclusion: Embracing the Ambiguity and the Power of Exploration
The sequence "8x 2, 10, 6x 2" serves as a compelling illustration of the complexity and beauty inherent in mathematics. While a definitive solution remains elusive without further context, the exploration itself has illuminated various mathematical concepts, from simple arithmetic to the importance of pattern recognition and the crucial role of context in problem-solving. This analysis underlines the importance of a systematic and flexible approach, embracing the ambiguity inherent in many mathematical puzzles and the power of exploration in uncovering their hidden depths. The seemingly simple sequence has led us on a journey of mathematical discovery, showcasing the richness and intrigue of the subject. Further analysis requires more information, highlighting the vital role of context in deciphering mathematical enigmas.
Latest Posts
Latest Posts
-
Ca3 Po4 2 Molar Mass
Sep 12, 2025
-
A Retractable Service Pit Cover
Sep 12, 2025
-
What Is 20 Of 21
Sep 12, 2025
-
Given Abcd Solve For X
Sep 12, 2025
-
What Is A Unique Polygon
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 8x 2 10 6x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.