9 16 As A Decimal
cibeltiagestion
Sep 02, 2025 · 5 min read
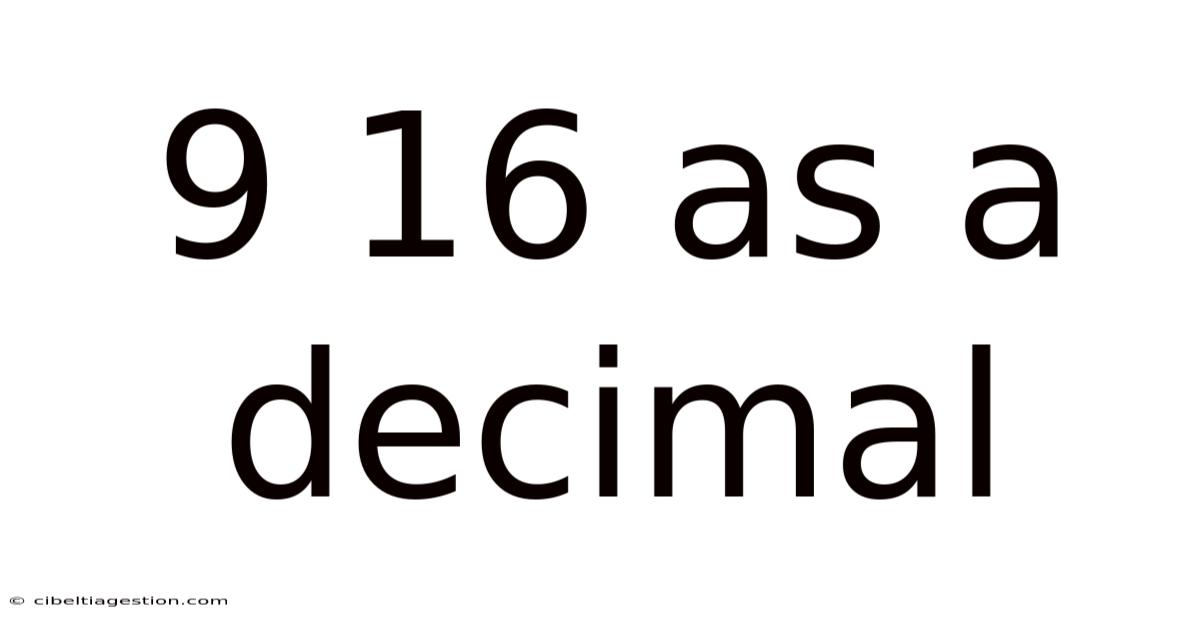
Table of Contents
Unveiling the Mystery: 9/16 as a Decimal and Beyond
Understanding fractions and their decimal equivalents is fundamental to mathematics and numerous real-world applications. This comprehensive guide delves into the conversion of the fraction 9/16 to its decimal form, exploring the process, underlying principles, and practical implications. We'll move beyond a simple answer, providing a deeper understanding of fraction-to-decimal conversion and related concepts. This will equip you with the skills to tackle similar conversions confidently.
Introduction: From Fractions to Decimals
Fractions and decimals are two different ways of representing parts of a whole. A fraction expresses a part as a ratio of two numbers (numerator and denominator), while a decimal uses a base-ten system with a decimal point to represent parts of a whole. Converting between these two forms is a crucial skill in mathematics. This article focuses on converting the fraction 9/16 to a decimal, explaining the method in detail and exploring the broader context of this fundamental mathematical operation. We'll cover not only the calculation itself but also the underlying mathematical principles and practical examples where this conversion is useful. The keyword here is understanding, not just memorization.
Method 1: Long Division
The most straightforward way to convert 9/16 to a decimal is through long division. This involves dividing the numerator (9) by the denominator (16).
-
Set up the division: Write 9 as the dividend and 16 as the divisor. Add a decimal point after 9 and add zeros as needed to continue the division.
-
Perform the division: 16 does not go into 9, so we add a zero and a decimal point to 9, making it 9.0. 16 goes into 90 five times (16 x 5 = 80). Write 5 above the decimal point in the quotient.
-
Subtract and bring down: Subtract 80 from 90, leaving 10. Bring down another zero to make it 100.
-
Continue dividing: 16 goes into 100 six times (16 x 6 = 96). Write 6 in the quotient.
-
Subtract and bring down: Subtract 96 from 100, leaving 4. Bring down another zero to make it 40.
-
Final steps: 16 goes into 40 two times (16 x 2 = 32). Write 2 in the quotient. Subtract 32 from 40, leaving 8. Bring down another zero to make it 80. 16 goes into 80 five times (16 x 5 = 80). Subtract 80 from 80, leaving 0. The division is complete.
Therefore, 9/16 = 0.5625.
Method 2: Converting to an Equivalent Fraction with a Power of 10 Denominator
While long division is effective, another approach involves converting 9/16 into an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). However, this is not directly possible for 9/16, as 16 does not divide evenly into any power of 10. This method is more practical for fractions with denominators that have factors of 2 and/or 5.
Method 3: Using a Calculator
The simplest method is using a calculator. Simply enter 9 ÷ 16 and the calculator will display the decimal equivalent, 0.5625. While convenient, understanding the underlying process remains crucial for developing a strong mathematical foundation.
Understanding the Decimal Result: 0.5625
The decimal 0.5625 represents 5625 ten-thousandths. This can be expressed as:
- 5 tenths (0.5)
- 6 hundredths (0.06)
- 2 thousandths (0.002)
- 5 ten-thousandths (0.0005)
Adding these together confirms the value of 0.5625.
Practical Applications of Decimal Conversions
The conversion of fractions to decimals is essential in numerous real-world situations:
-
Finance: Calculating percentages, interest rates, and discounts often involve converting fractions to decimals. For example, a 9/16 inch measurement needs to be translated into decimals for precise engineering or carpentry work.
-
Measurement: Many measurements use decimal systems (metric system). Converting fractional measurements to decimals is crucial for accuracy and compatibility.
-
Science: Scientific calculations frequently involve decimal numbers. Converting fractions to decimals simplifies calculations and ensures consistent units.
-
Computer Programming: Computers work primarily with decimal numbers. Converting fractions to decimals is essential for programming applications that handle fractional data.
-
Everyday Life: From baking recipes (measuring ingredients) to calculating fuel efficiency, understanding decimal equivalents of fractions is highly useful.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to learn fraction-to-decimal conversions?
- A: Mastering this skill is fundamental for proficiency in mathematics and its applications in various fields. It's crucial for accurate calculations, problem-solving, and understanding numerical relationships.
-
Q: Are there other fractions that are easily converted to decimals?
- A: Yes, fractions with denominators that are powers of 10 (10, 100, 1000, etc.) or have only 2 and 5 as prime factors convert easily to terminating decimals. For example, 1/2 = 0.5, 3/4 = 0.75, 7/10 = 0.7.
-
Q: What if the fraction results in a repeating decimal?
- A: Some fractions result in non-terminating, repeating decimals (e.g., 1/3 = 0.333...). These are handled differently, often represented with a bar over the repeating digits (0.3̅).
-
Q: Can I use a calculator for all fraction-to-decimal conversions?
- A: While calculators are useful tools, understanding the underlying mathematical principles of long division is essential for a deep understanding of the conversion process and its application in various situations.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions to decimals is a vital skill in mathematics and beyond. This article explored the various methods for converting 9/16 to its decimal equivalent (0.5625), emphasizing both the practical calculation and the underlying mathematical concepts. Understanding this process empowers you to handle similar conversions confidently, enhancing your mathematical skills and problem-solving abilities across various disciplines. Remember, practice is key to mastering this important skill. Try converting other fractions to decimals using the methods described above to reinforce your understanding and build confidence in your mathematical abilities. The more you practice, the more intuitive this process will become, making it an invaluable tool in your mathematical toolkit.
Latest Posts
Latest Posts
-
Fatigue Is Considered An Impairment
Sep 02, 2025
-
Is Alcohol Homogeneous Or Heterogeneous
Sep 02, 2025
-
When Should Thermometers Be Recalibrated
Sep 02, 2025
-
What Is 10 Of 1200
Sep 02, 2025
-
27 50 As A Decimal
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about 9 16 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.