9 Times What Equals 72
cibeltiagestion
Sep 07, 2025 · 5 min read
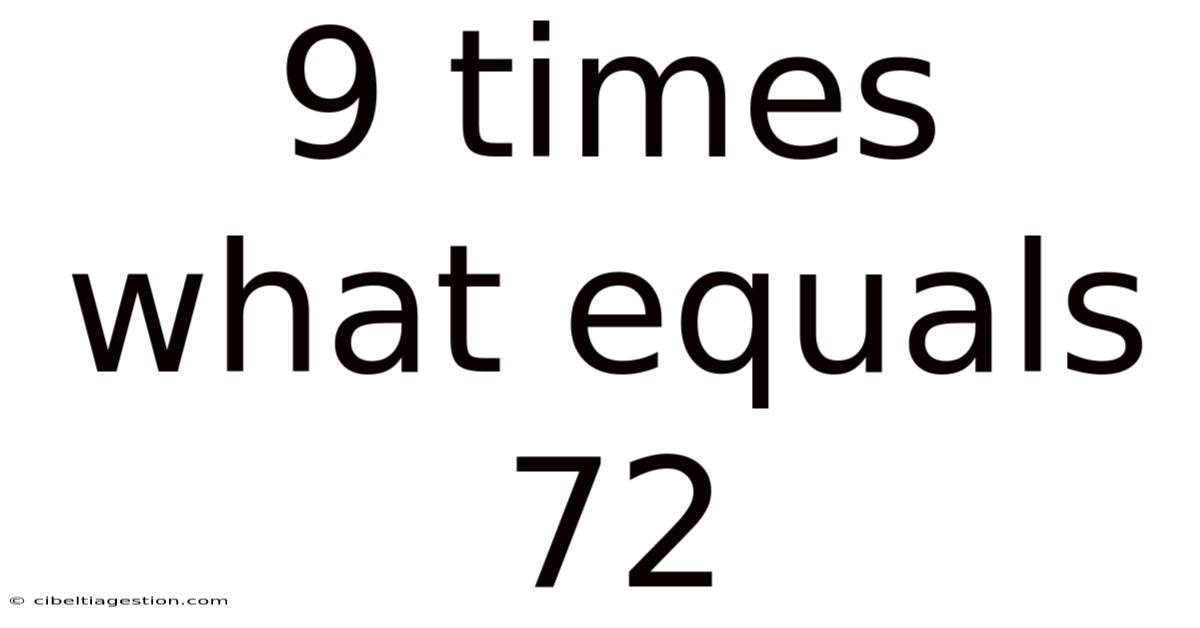
Table of Contents
Unlocking the Mystery: 9 Times What Equals 72? A Deep Dive into Multiplication
This article explores the seemingly simple question, "9 times what equals 72?" While the answer itself is straightforward, we'll delve deeper than a simple calculation. We'll unpack the underlying mathematical concepts, explore different methods to solve this type of problem, and even touch upon the broader applications of multiplication in everyday life. This comprehensive guide is designed for anyone, from elementary school students solidifying their multiplication skills to adults seeking to refresh their foundational math knowledge.
Understanding the Problem: 9 x ? = 72
The core of the problem lies in understanding multiplication as repeated addition. The equation "9 times what equals 72" can be rephrased as: "What number, added to itself nine times, equals 72?" This rephrasing helps visualize the operation and provides a more intuitive understanding for those who may struggle with the abstract nature of multiplication. The question is essentially asking us to find the missing factor in a multiplication equation.
Methods to Solve: Finding the Missing Factor
Several methods can efficiently solve for the missing factor in "9 x ? = 72." Let's explore some common approaches:
1. Direct Division: The most straightforward method involves dividing 72 by 9. This is the inverse operation of multiplication. The calculation is: 72 ÷ 9 = 8. Therefore, 9 times 8 equals 72.
2. Repeated Subtraction: Imagine you have 72 objects, and you want to divide them into 9 equal groups. You can repeatedly subtract 9 from 72 until you reach zero. The number of times you subtract 9 represents the size of each group. Let's illustrate:
- 72 - 9 = 63
- 63 - 9 = 54
- 54 - 9 = 45
- 45 - 9 = 36
- 36 - 9 = 27
- 27 - 9 = 18
- 18 - 9 = 9
- 9 - 9 = 0
You subtracted 9 eight times, confirming that 9 x 8 = 72. While effective, this method is less efficient for larger numbers.
3. Multiplication Table Recall: If you have memorized your multiplication tables, you'll instantly recognize that 9 x 8 = 72. Memorizing multiplication tables is a fundamental skill that significantly speeds up calculations and improves mathematical fluency.
4. Using a Calculator: For more complex multiplication problems, a calculator provides a quick and accurate solution. Simply input 72 ÷ 9 to obtain the answer, 8. While convenient, relying solely on calculators can hinder the development of essential mental math skills.
Beyond the Basics: Exploring Multiplication Concepts
Solving "9 times what equals 72" opens doors to a deeper understanding of fundamental mathematical concepts. Let's explore some of them:
1. Commutative Property: The commutative property of multiplication states that changing the order of factors does not change the product. This means 9 x 8 is the same as 8 x 9. Both equal 72. Understanding this property enhances flexibility in problem-solving.
2. Associative Property: The associative property applies when multiplying more than two numbers. It states that the grouping of factors doesn't affect the product. For example, (9 x 2) x 4 = 9 x (2 x 4) = 72.
3. Distributive Property: The distributive property explains how multiplication interacts with addition (and subtraction). It states that multiplying a number by a sum is the same as multiplying the number by each addend and then adding the products. For example, 9 x (4 + 4) = (9 x 4) + (9 x 4) = 72.
4. Factors and Multiples: In the equation 9 x 8 = 72, 9 and 8 are factors of 72, and 72 is a multiple of both 9 and 8. Understanding factors and multiples is crucial for various mathematical concepts, including prime factorization and finding least common multiples.
5. Inverse Operations: Division is the inverse operation of multiplication. This means that division "undoes" multiplication, and vice-versa. This inverse relationship is fundamental to solving equations and understanding mathematical relationships.
Real-World Applications of Multiplication
Multiplication is far from a purely academic exercise; it's a fundamental tool used extensively in everyday life. Here are just a few examples:
-
Shopping: Calculating the total cost of multiple items of the same price. For example, if apples cost $2 each, and you buy 9 apples, you'd multiply 2 x 9 to find the total cost ($18).
-
Cooking: Scaling recipes. If a recipe calls for 3 cups of flour and you want to double the recipe, you'd multiply all ingredient quantities by 2.
-
Construction: Calculating the area of a room or the volume of a container. Area is calculated by multiplying length by width, and volume is length x width x height.
-
Finance: Calculating interest, discounts, or taxes. These calculations often involve multiplication.
-
Travel: Determining the total distance traveled based on speed and time. Distance = speed x time.
Frequently Asked Questions (FAQ)
Q: Are there other numbers that, when multiplied by 9, equal 72?
A: No. Multiplication is a one-to-one operation; only one number (8 in this case) will satisfy the equation 9 x ? = 72.
Q: What if the problem was 72 divided by what equals 9?
A: This is the inverse operation. You'd solve it by dividing 72 by 9 to find the answer, which is 8.
Q: How can I improve my multiplication skills?
A: Practice is key. Regularly work through multiplication problems, memorize multiplication tables, use flashcards, and try different methods to solve problems. Online resources and math games can also be very helpful.
Q: Is there a way to solve this problem without division?
A: While division is the most efficient method, you can use repeated subtraction or refer to a multiplication table. However, these methods become less practical with larger numbers.
Conclusion: Mastering Multiplication – One Step at a Time
The seemingly simple question, "9 times what equals 72?" provides a gateway to understanding crucial mathematical concepts. From the basic operation of multiplication to the more advanced properties and real-world applications, this problem highlights the importance of a solid foundation in mathematics. Mastering multiplication not only improves calculation skills but also enhances problem-solving abilities and strengthens critical thinking in various aspects of life. Remember, consistent practice and a curious mind are the keys to unlocking mathematical fluency and confidence. So, keep exploring, keep practicing, and keep discovering the fascinating world of numbers!
Latest Posts
Latest Posts
-
Sighting In A Rifle Means
Sep 07, 2025
-
Schedule Promocion Perezoso Horario Impuestos
Sep 07, 2025
-
Automated Vehicles Decrease Independent Transportation
Sep 07, 2025
-
Sodium Bicarbonate And Sulfuric Acid
Sep 07, 2025
-
When Does Interest Group Capture Occur
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 9 Times What Equals 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.