Factor 4x 2 X 5
cibeltiagestion
Sep 15, 2025 · 5 min read
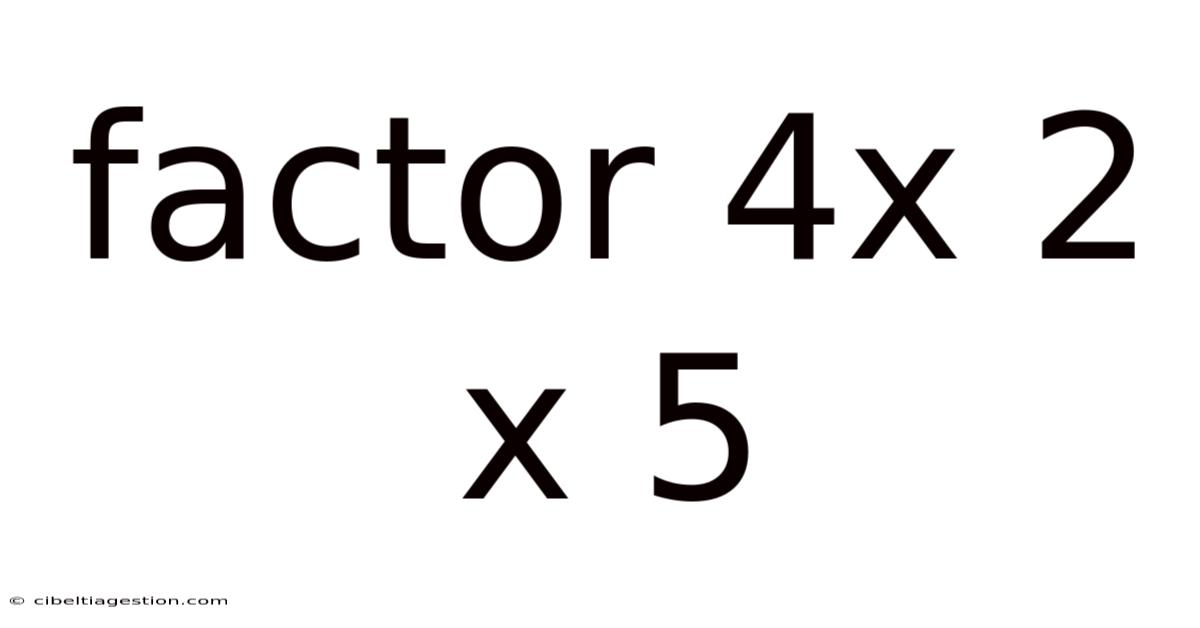
Table of Contents
Decoding Factorials: A Deep Dive into 4! x 2! x 5!
Understanding factorials is crucial in various fields, from mathematics and statistics to computer science and even some areas of physics. This article provides a comprehensive exploration of factorials, focusing on the calculation and implications of 4! x 2! x 5!. We'll cover the fundamental definition, step-by-step calculation methods, explore the underlying mathematical principles, and address frequently asked questions. By the end, you'll not only be able to calculate this specific expression but also possess a robust understanding of factorial notation and its applications.
What is a Factorial?
The factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. In simpler terms, it's the result of multiplying all whole numbers from 1 up to n. For example:
- 1! = 1
- 2! = 2 x 1 = 2
- 3! = 3 x 2 x 1 = 6
- 4! = 4 x 3 x 2 x 1 = 24
- 5! = 5 x 4 x 3 x 2 x 1 = 120
The factorial of 0, denoted as 0!, is defined as 1. This might seem counterintuitive at first, but it's necessary for maintaining consistency in mathematical formulas and theorems. We'll delve deeper into the reasoning behind this definition later.
Calculating 4! x 2! x 5! Step-by-Step
Now, let's tackle the main problem: calculating 4! x 2! x 5!. We'll break it down into manageable steps:
-
Calculate 4!: As shown above, 4! = 4 x 3 x 2 x 1 = 24
-
Calculate 2!: Similarly, 2! = 2 x 1 = 2
-
Calculate 5!: 5! = 5 x 4 x 3 x 2 x 1 = 120
-
Multiply the results: Finally, multiply the results of each individual factorial: 24 x 2 x 120 = 5760
Therefore, 4! x 2! x 5! = 5760.
Deeper Dive into Factorial Mathematics
Factorials are fundamental in various areas of mathematics. Their significance stems from their connection to permutations and combinations.
-
Permutations: A permutation is an arrangement of objects in a specific order. If you have n distinct objects, the number of ways you can arrange them is n!. For example, if you have 4 distinct books, there are 4! = 24 different ways to arrange them on a shelf.
-
Combinations: A combination is a selection of objects where the order doesn't matter. The number of ways to choose k objects from a set of n objects is given by the binomial coefficient, often written as ⁿCₖ or (ⁿₖ), which is calculated as n! / (k! * (n-k)!). Factorials are essential components of this formula.
-
Series and Expansions: Factorials appear frequently in infinite series expansions of important functions, such as the Taylor series expansion of the exponential function (eˣ) and the trigonometric functions (sin x, cos x).
-
Probability and Statistics: Factorials play a crucial role in probability calculations, particularly when dealing with permutations and combinations in probability problems. For instance, calculating the probability of drawing specific cards from a deck involves using factorials.
-
Gamma Function: The factorial function can be extended to non-integer values using the Gamma function (Γ(z)). The Gamma function is a complex function that generalizes the factorial to complex numbers. Γ(n) = (n-1)! for positive integers n.
Why is 0! = 1?
The definition of 0! = 1 might seem arbitrary, but it's crucial for maintaining consistency and avoiding exceptions in mathematical formulas. Consider the following:
-
Combinations: Recall the formula for combinations: n! / (k! * (n-k)!). If we have n objects and want to choose 0 objects (i.e., k=0), the formula should still work. To make this work, we must define 0! as 1. Otherwise, the formula would be undefined.
-
Empty Product: A factorial can be seen as a product. The product of no numbers is defined as 1 (the multiplicative identity). This is analogous to the sum of no numbers being defined as 0 (the additive identity).
-
Recursive Definition: The factorial function can also be defined recursively: n! = n * (n-1)!. If we apply this definition repeatedly, we eventually reach 1! = 1 * 0!. For the recursive definition to hold for all non-negative integers, 0! must equal 1.
Frequently Asked Questions (FAQ)
Q: Can you calculate factorials for negative numbers?
A: No, the factorial function is not defined for negative integers. The Gamma function extends the factorial function to complex numbers, including negative non-integers, but it doesn't provide a value for negative integers.
Q: Are there any shortcuts for calculating large factorials?
A: Calculating very large factorials directly can be computationally intensive. Approximation methods, such as Stirling's approximation, are often used for large values of n. Stirling's approximation provides a good estimate of n! when n is large.
Q: What are some real-world applications of factorials?
A: Factorials find applications in numerous fields:
- Cryptography: Factorials are used in certain cryptographic algorithms.
- Computer science: Factorials are important in algorithms dealing with permutations and combinations.
- Physics: Factorials are used in quantum mechanics and statistical mechanics.
- Probability and statistics: Essential for calculating probabilities related to arrangements and selections.
- Scheduling and logistics: Used in optimizing schedules and delivery routes.
Q: How do I use a calculator or computer program to calculate factorials?
A: Most scientific calculators and programming languages (like Python, Java, and MATLAB) have built-in functions to calculate factorials. In Python, for example, you would use the math.factorial() function.
Conclusion
Understanding factorials goes beyond simply memorizing the calculation. It's about grasping their deep connection to fundamental mathematical concepts like permutations, combinations, and series expansions. The calculation of 4! x 2! x 5! = 5760 serves as a practical illustration of these concepts. This comprehensive exploration should provide a solid foundation for anyone seeking to delve deeper into the fascinating world of factorials and their applications in various fields. Remember, mastering factorials is not just about numbers; it's about unlocking the power of mathematical reasoning and problem-solving. From simple calculations to complex applications, factorials provide a powerful tool for understanding and tackling mathematical challenges.
Latest Posts
Latest Posts
-
Height 65 Inches In Feet
Sep 16, 2025
-
13 Times 13 Times 13
Sep 16, 2025
-
How To Unblur Course Hero
Sep 16, 2025
-
This Account Is Inactive Mychaetr
Sep 16, 2025
-
Lewis Dot Structure For Sbr2
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor 4x 2 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.