Factor X 2 2x 3
cibeltiagestion
Sep 11, 2025 · 6 min read
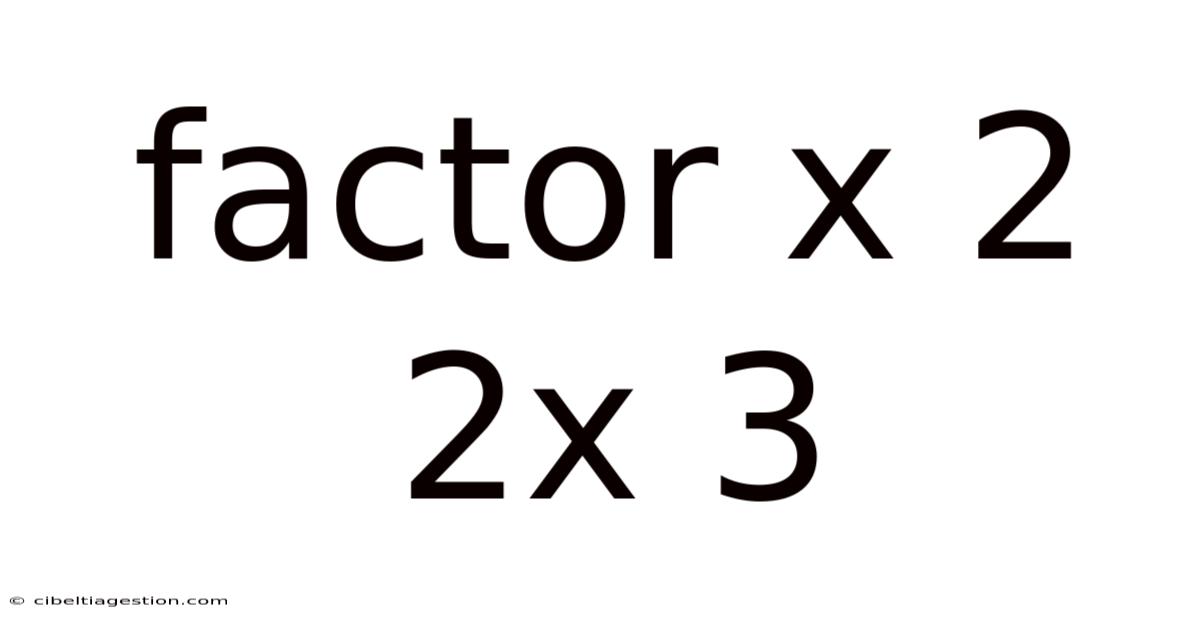
Table of Contents
Understanding and Solving Factor x² + 2x - 3
This article will delve into the intricacies of factoring the quadratic expression x² + 2x - 3, providing a comprehensive guide suitable for students and anyone seeking a deeper understanding of algebraic manipulation. We'll explore various methods, including factoring by grouping, the quadratic formula, and graphical representation, to illustrate the different approaches to solving this seemingly simple yet fundamentally important problem in algebra. Understanding this concept is crucial for further advancements in mathematics, particularly in calculus and beyond.
Introduction: What is Factoring?
Factoring, in algebra, is the process of breaking down a mathematical expression into simpler components that, when multiplied together, yield the original expression. It's like reverse multiplication. For instance, factoring 6 would give you 2 x 3. In the case of quadratic expressions like x² + 2x - 3, we aim to find two binomial expressions whose product equals the original quadratic. This process is essential for solving quadratic equations, simplifying expressions, and understanding the behavior of functions.
Method 1: Factoring by Grouping (for simpler quadratics)
This method is particularly effective for quadratic expressions where the coefficient of x² is 1. Let's apply it to x² + 2x - 3:
-
Identify the factors of the constant term: The constant term in our expression is -3. We need to find two numbers that multiply to -3 and add up to the coefficient of the x term, which is 2. These numbers are 3 and -1. (3 x -1 = -3 and 3 + (-1) = 2).
-
Rewrite the expression: Rewrite the expression x² + 2x - 3 using these factors: x² + 3x - x - 3
-
Group the terms: Group the terms in pairs: (x² + 3x) + (-x - 3)
-
Factor out the common factor from each group: In the first group, x is the common factor; in the second group, -1 is the common factor: x(x + 3) - 1(x + 3)
-
Factor out the common binomial: Notice that (x + 3) is a common factor in both terms. Factor it out: (x + 3)(x - 1)
Therefore, the factored form of x² + 2x - 3 is (x + 3)(x - 1).
Method 2: The Quadratic Formula (for more complex quadratics)
The quadratic formula is a powerful tool that can be used to factor any quadratic expression, even those where factoring by grouping is more difficult or impossible. The general form of a quadratic equation is ax² + bx + c = 0. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Let's apply this to our expression x² + 2x - 3. First, we rewrite it as a quadratic equation: x² + 2x - 3 = 0. In this case, a = 1, b = 2, and c = -3.
Substituting these values into the quadratic formula:
x = [-2 ± √(2² - 4 * 1 * -3)] / (2 * 1) x = [-2 ± √(4 + 12)] / 2 x = [-2 ± √16] / 2 x = [-2 ± 4] / 2
This gives us two solutions:
x = (-2 + 4) / 2 = 1 x = (-2 - 4) / 2 = -3
These solutions represent the roots or zeros of the quadratic equation. To obtain the factored form, we can express these roots as factors:
(x - 1)(x + 3)
Again, we arrive at the factored form (x + 3)(x - 1). Note that the order of the factors doesn't matter; (x - 1)(x + 3) is equivalent to (x + 3)(x - 1).
Method 3: Graphical Representation (visualizing the roots)
Graphing the quadratic function y = x² + 2x - 3 provides a visual representation of the roots. The x-intercepts (where the graph intersects the x-axis) represent the solutions to the equation x² + 2x - 3 = 0. These x-intercepts correspond to the factors.
By plotting the graph, you would observe that the parabola intersects the x-axis at x = 1 and x = -3. These points directly translate to the factors (x - 1) and (x + 3). Therefore, the factored form is again (x + 3)(x - 1). This method offers a geometrical understanding of factoring and is helpful for visualizing the relationship between the roots and the factors.
Understanding the Significance of Factoring
Factoring quadratic expressions like x² + 2x - 3 is not just an algebraic exercise; it holds significant importance in various mathematical applications. Here are some key reasons:
-
Solving Quadratic Equations: Finding the factors allows us to solve quadratic equations easily. If (x + 3)(x - 1) = 0, then either (x + 3) = 0 or (x - 1) = 0, giving us the solutions x = -3 and x = 1.
-
Simplifying Expressions: Factoring can simplify complex algebraic expressions, making them easier to manipulate and analyze.
-
Finding the Roots of a Function: The roots (or zeros) of a quadratic function represent the points where the graph intersects the x-axis. Factoring helps us identify these points directly.
-
Sketching Graphs of Quadratic Functions: Knowing the roots allows for quick and accurate sketching of the parabola representing the quadratic function. The vertex of the parabola can also be easily determined using the factored form.
-
Applications in Calculus: Factoring is fundamental in calculus, particularly when dealing with derivatives, integrals, and solving optimization problems.
Frequently Asked Questions (FAQ)
-
What if the quadratic expression doesn't factor easily? If factoring by grouping is difficult, use the quadratic formula. This method works for all quadratic expressions.
-
Can a quadratic expression have only one factor? Yes, a quadratic expression can have only one factor (a repeated root) if the discriminant (b² - 4ac) is equal to zero. This results in a perfect square trinomial.
-
What is the discriminant, and why is it important? The discriminant (b² - 4ac) in the quadratic formula determines the nature of the roots. If it's positive, there are two distinct real roots; if it's zero, there's one real root (repeated); and if it's negative, there are two complex roots.
-
How can I check if my factoring is correct? Simply expand the factored form using the distributive property (FOIL). If you get back the original quadratic expression, your factoring is correct.
-
Are there other methods for factoring quadratics? Yes, while the methods described above are common, other advanced techniques exist for factoring more complex quadratics or higher-degree polynomials. These often involve substitution or the use of specialized algorithms.
Conclusion: Mastering the Art of Factoring
Mastering the art of factoring quadratic expressions is a cornerstone of algebraic proficiency. The ability to factor x² + 2x - 3, and other similar expressions, lays the groundwork for tackling more complex mathematical concepts. By understanding the different methods – factoring by grouping, the quadratic formula, and graphical representation – you equip yourself with versatile tools to approach a wide array of algebraic problems. Remember to practice consistently, and don't hesitate to explore further resources to deepen your understanding. The seemingly simple act of factoring unlocks a world of mathematical possibilities. It's a skill that will continuously serve you well throughout your mathematical journey, from solving simple equations to tackling advanced calculus problems. The more you practice, the more intuitive and effortless this process will become, providing a strong foundation for success in your mathematical endeavors.
Latest Posts
Latest Posts
-
What Has Wheels And Flies
Sep 11, 2025
-
Which Species Has 54 Electrons
Sep 11, 2025
-
Earths Main Energy Outputs Are
Sep 11, 2025
-
Y 1 2x 1 Graph
Sep 11, 2025
-
Which Statements Characterize Articular Cartilage
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 2x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.