Factor X 2 3x 28
cibeltiagestion
Sep 13, 2025 · 5 min read
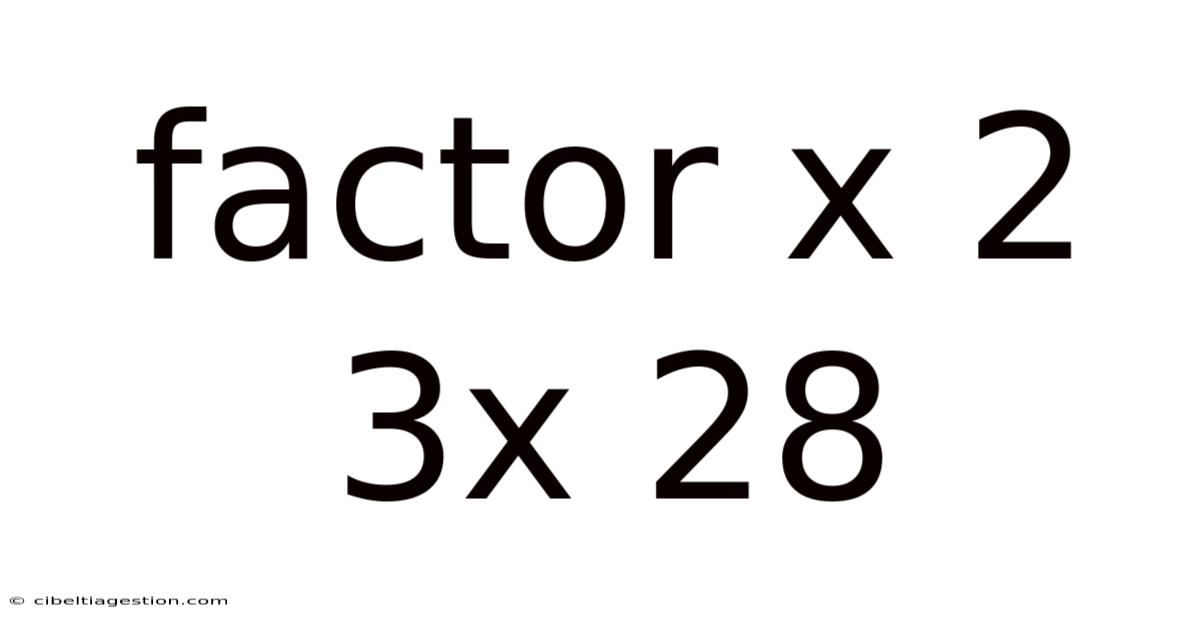
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into x² + 3x - 28
Understanding how to factor quadratic expressions is a fundamental skill in algebra. This seemingly simple process unlocks the door to solving complex equations, graphing parabolas, and tackling a wide range of mathematical problems. This comprehensive guide will explore the factoring of the quadratic expression x² + 3x - 28, providing a step-by-step approach, exploring the underlying mathematical principles, and answering frequently asked questions. We'll move beyond simply finding the answer to develop a deeper understanding of the why behind the method.
Understanding Quadratic Expressions
Before diving into the factoring process, let's establish a common understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. The general form is ax² + bx + c, where a, b, and c are constants, and a ≠ 0. In our case, we're dealing with x² + 3x - 28, where a = 1, b = 3, and c = -28.
Factoring x² + 3x - 28: A Step-by-Step Approach
Factoring a quadratic expression means rewriting it as a product of two simpler expressions (usually binomials). There are several methods to achieve this, but for x² + 3x - 28, the most straightforward approach is the "AC method" or finding two numbers that add up to 'b' and multiply to 'ac'.
Step 1: Identify a, b, and c
In our expression, x² + 3x - 28, we have:
- a = 1
- b = 3
- c = -28
Step 2: Find two numbers that add up to 'b' and multiply to 'ac'
We need to find two numbers that add up to 3 (our 'b' value) and multiply to -28 (our 'ac' value, which is 1 * -28 = -28). Let's list the factor pairs of -28:
- 1 and -28
- -1 and 28
- 2 and -14
- -2 and 14
- 4 and -7
- -4 and 7
The pair that adds up to 3 is 7 and -4.
Step 3: Rewrite the expression using the two numbers found in Step 2
We replace the middle term (3x) with the two numbers we found (7x and -4x):
x² + 7x - 4x - 28
Step 4: Factor by grouping
Now, we group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
x(x + 7) - 4(x + 7)
Notice that (x + 7) is a common factor in both terms.
Step 5: Factor out the common binomial
We factor out (x + 7):
(x + 7)(x - 4)
Therefore, the factored form of x² + 3x - 28 is (x + 7)(x - 4).
Verification: Expanding the Factored Form
To verify our answer, we can expand the factored form using the FOIL method (First, Outer, Inner, Last):
(x + 7)(x - 4) = x² - 4x + 7x - 28 = x² + 3x - 28
This matches our original expression, confirming that our factoring is correct.
The Underlying Mathematical Principles
The success of this factoring method relies on the distributive property of multiplication. When we expand (x + 7)(x - 4), we're essentially applying the distributive property twice:
- First, we distribute (x + 7) over (x - 4): (x + 7)x + (x + 7)(-4)
- Then, we distribute x and -4 over (x + 7): x² + 7x - 4x - 28
This process reverses when we factor, demonstrating the elegance and power of algebraic manipulation.
Solving Quadratic Equations using Factoring
Factoring quadratic expressions is crucial for solving quadratic equations. A quadratic equation is an equation of the form ax² + bx + c = 0. To solve it, we set the quadratic expression equal to zero and then factor it. The solutions (roots or zeros) are the values of x that make the equation true.
For example, to solve x² + 3x - 28 = 0, we use the factored form:
(x + 7)(x - 4) = 0
This equation is true if either (x + 7) = 0 or (x - 4) = 0. Solving these simpler equations gives us the solutions:
- x = -7
- x = 4
These are the roots of the quadratic equation. They represent the x-intercepts of the parabola represented by the quadratic function y = x² + 3x - 28.
Alternative Factoring Methods
While the AC method is effective for many quadratic expressions, especially those with a leading coefficient of 1, other methods exist:
-
Trial and Error: This involves directly guessing the binomial factors based on the factors of 'a' and 'c'. This method can be quicker for simpler expressions but less systematic for more complex ones.
-
Completing the Square: This method involves manipulating the quadratic expression to create a perfect square trinomial, which can then be easily factored. It's particularly useful when the quadratic expression doesn't factor easily using other methods.
-
Quadratic Formula: This is a general formula that provides the solutions to any quadratic equation, regardless of whether it factors easily or not. It's a powerful tool, but it doesn't directly give the factored form of the expression.
Frequently Asked Questions (FAQs)
Q1: What if the quadratic expression doesn't factor easily?
A1: If the quadratic expression doesn't factor easily using the AC method or trial and error, you can use the quadratic formula to find the solutions. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Q2: Can I factor x² + 3x - 28 in a different way?
A2: While (x + 7)(x - 4) is the most common and straightforward factorization, the order of the factors doesn't matter. (x - 4)(x + 7) is equally valid.
Q3: What does factoring tell us about the graph of a quadratic function?
A3: Factoring a quadratic expression reveals the x-intercepts (roots) of the corresponding quadratic function. These are the points where the parabola intersects the x-axis.
Conclusion
Factoring quadratic expressions, like x² + 3x - 28, is a fundamental algebraic skill with broad applications. Understanding the underlying principles, mastering the techniques (like the AC method), and practicing regularly will build a strong foundation for more advanced algebraic concepts. While the process might seem initially challenging, the ability to break down complex expressions into simpler forms provides a satisfying sense of accomplishment and unlocks deeper understanding within the realm of mathematics. Remember to practice consistently – the more you work with these techniques, the more intuitive they will become.
Latest Posts
Latest Posts
-
How Long Is 4 Score
Sep 13, 2025
-
Is 128 Oz A Gallon
Sep 13, 2025
-
Nad Medical Abbreviation Physical Exam
Sep 13, 2025
-
How Tall Is 73 Inches
Sep 13, 2025
-
Water Has Surface Tension Because
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 3x 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.