Factor X 2 6x 9
cibeltiagestion
Sep 16, 2025 · 6 min read
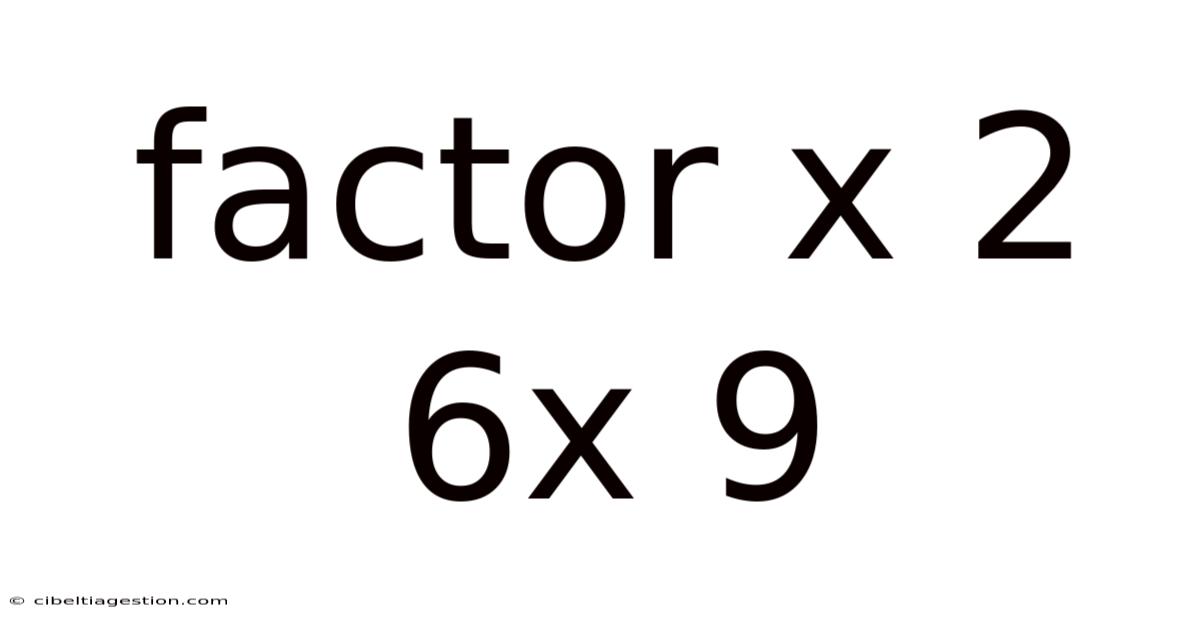
Table of Contents
Factoring the Quadratic Expression: x² + 6x + 9
This article explores the factoring of the quadratic expression x² + 6x + 9. We'll delve into the process step-by-step, explaining the underlying mathematical principles, and provide various approaches to solving similar problems. Understanding quadratic equations and their factorization is fundamental to higher-level mathematics and numerous applications in science and engineering. This comprehensive guide will equip you with the tools to confidently tackle such problems.
Introduction to Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. The general form of a quadratic expression is ax² + bx + c, where a, b, and c are constants, and a ≠ 0. Factoring a quadratic expression means rewriting it as a product of two simpler expressions, often linear expressions (expressions of degree one). This process is crucial in solving quadratic equations and simplifying algebraic expressions.
Our specific example, x² + 6x + 9, falls neatly into this category. The values of a, b, and c are 1, 6, and 9 respectively. Notice the special relationship between these coefficients – this expression is a perfect square trinomial.
Method 1: Recognizing a Perfect Square Trinomial
The expression x² + 6x + 9 is a perfect square trinomial. This means it can be factored into the square of a binomial. A perfect square trinomial always follows the pattern:
a² + 2ab + b² = (a + b)² or a² - 2ab + b² = (a - b)²
Let's see how this applies to our expression:
- Identify a and b: In x² + 6x + 9, we can see that x² is the square of x (a = x), and 9 is the square of 3 (b = 3).
- Check the middle term: The middle term, 6x, is equal to 2ab: 2 * x * 3 = 6x.
- Factor the expression: Since the pattern matches a perfect square trinomial with a positive middle term, we can factor it as (x + 3)².
Therefore, the factored form of x² + 6x + 9 is (x + 3)(x + 3) = (x + 3)².
Method 2: Using the FOIL Method in Reverse
The FOIL method (First, Outer, Inner, Last) is commonly used to expand binomials. We can use it in reverse to factor quadratic expressions. Let's assume the factored form is (x + p)(x + q), where p and q are constants we need to find.
Expanding (x + p)(x + q) using FOIL, we get:
x² + qx + px + pq = x² + (p + q)x + pq
Comparing this to our original expression, x² + 6x + 9, we can establish the following equations:
- p + q = 6
- pq = 9
We need to find two numbers (p and q) that add up to 6 and multiply to 9. The numbers 3 and 3 satisfy these conditions:
- 3 + 3 = 6
- 3 * 3 = 9
Therefore, the factored form is (x + 3)(x + 3) = (x + 3)².
Method 3: Completing the Square
Completing the square is a general method for solving quadratic equations and factoring quadratic expressions. This method involves manipulating the expression to create a perfect square trinomial.
- Focus on the x² and x terms: Consider the first two terms of x² + 6x + 9: x² + 6x.
- Find the value to complete the square: To complete the square, take half of the coefficient of the x term (6/2 = 3), square it (3² = 9), and add it to the expression. Notice that we already have a 9 in our original expression.
- Rewrite as a perfect square: x² + 6x + 9 can now be written as (x + 3)².
This confirms that the factored form is (x + 3)².
Method 4: Quadratic Formula (Indirect Approach)
While the quadratic formula is primarily used to find the roots (or zeros) of a quadratic equation, we can indirectly use it to find the factors.
The quadratic formula states that for the equation ax² + bx + c = 0, the roots are given by:
x = [-b ± √(b² - 4ac)] / 2a
For our expression x² + 6x + 9 = 0, a = 1, b = 6, and c = 9. Plugging these values into the quadratic formula, we get:
x = [-6 ± √(6² - 4 * 1 * 9)] / 2 * 1 = [-6 ± √0] / 2 = -3
Since the discriminant (b² - 4ac) is 0, there is only one real root, x = -3. This means the quadratic has a repeated root. A repeated root implies that the quadratic expression is a perfect square. Therefore, the factored form is (x + 3)².
Graphical Representation and Significance of the Roots
The graph of y = x² + 6x + 9 is a parabola that opens upwards. The fact that it factors to (x+3)² means that the parabola touches the x-axis at only one point, x = -3. This point is the vertex of the parabola, and it represents the only real root of the corresponding quadratic equation. This visual representation reinforces the concept of repeated roots.
Applications of Factoring Quadratic Expressions
Factoring quadratic expressions has numerous applications in various fields:
- Solving Quadratic Equations: Setting the factored expression equal to zero allows us to solve for the values of x that satisfy the equation.
- Calculus: Finding the roots of a quadratic is essential in optimization problems.
- Physics: Quadratic equations are frequently used in projectile motion calculations and other physical phenomena.
- Engineering: Designing structures, calculating areas, and many other engineering tasks involve quadratic equations.
- Computer Science: Quadratic equations are used in algorithms and data structures.
Frequently Asked Questions (FAQ)
-
Q: What if the quadratic expression doesn't factor easily?
- A: If the expression doesn't factor easily using simple methods, you can use the quadratic formula or completing the square to find the roots, which will then help you determine the factors. Sometimes, a quadratic expression may not factor into rational numbers; in such cases, irrational or complex roots are possible.
-
Q: Is there a way to check if my factoring is correct?
- A: Yes! You can always expand the factored form using the FOIL method or other distribution techniques. If you get back to the original quadratic expression, your factoring is correct.
-
Q: What's the difference between factoring and solving a quadratic equation?
- A: Factoring a quadratic expression is rewriting it as a product of simpler expressions. Solving a quadratic equation involves finding the values of x that make the equation true (i.e., make the expression equal to zero). Factoring helps in solving quadratic equations, but they are distinct processes.
-
Q: What if the coefficient of x² is not 1?
- A: If the coefficient of x² (the 'a' term) is not 1, the factoring process becomes slightly more complex but follows similar principles. You might need to use techniques like grouping or trial and error to find the appropriate factors.
Conclusion
Factoring the quadratic expression x² + 6x + 9 is straightforward due to its perfect square trinomial nature. We have explored multiple methods—recognizing perfect squares, reversing the FOIL method, completing the square, and indirectly utilizing the quadratic formula—demonstrating the versatility of approaches to solve such problems. Understanding these methods not only helps solve this specific problem but provides a strong foundation for tackling more complex quadratic expressions and their related applications in various mathematical and scientific domains. Remember to practice regularly to solidify your understanding and become proficient in factoring quadratic expressions. The more you practice, the more quickly you'll recognize patterns and efficiently apply these techniques.
Latest Posts
Latest Posts
-
10 0 4 0 5 G 4g
Sep 16, 2025
-
Subject Complements Are Words That
Sep 16, 2025
-
Crossword Puzzle For Respiratory System
Sep 16, 2025
-
20 Twenty Sevens Minus 1 Twenty Seven
Sep 16, 2025
-
200 Gm Sugar To Cups
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 6x 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.