Factorise X 2 4x 12
cibeltiagestion
Sep 11, 2025 · 6 min read
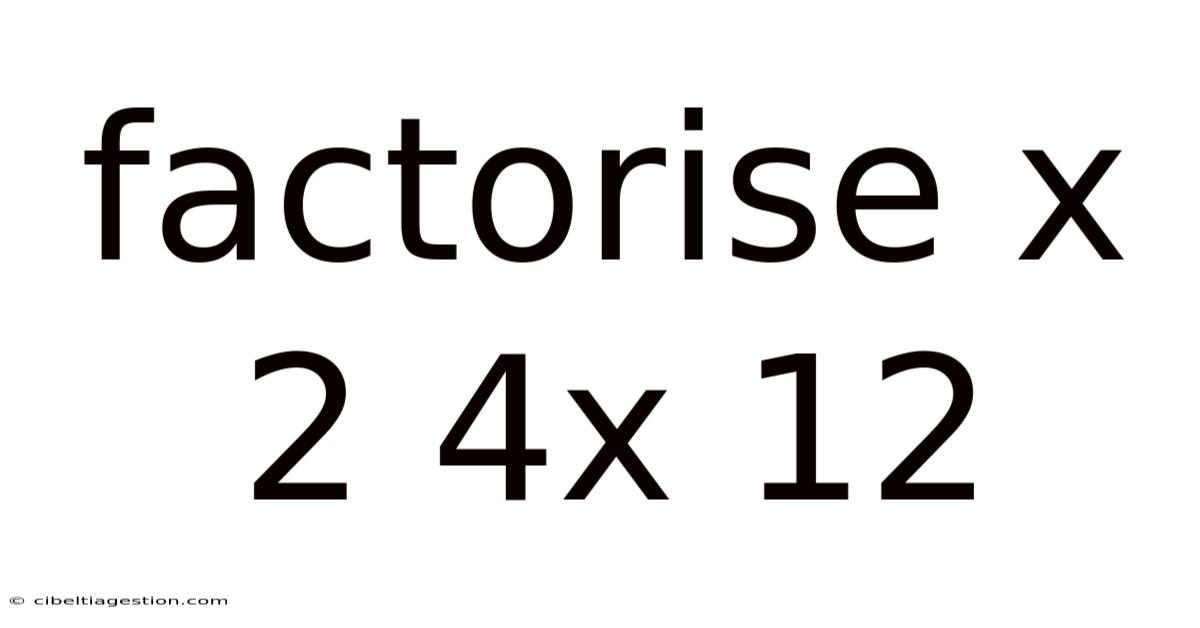
Table of Contents
Factorising Quadratic Expressions: A Deep Dive into x² + 4x + 12
This article provides a comprehensive guide on how to factorise the quadratic expression x² + 4x + 12. We'll explore various methods, discuss the underlying mathematical principles, and delve into why this particular expression presents a unique challenge. Understanding the process of factorisation is crucial for solving quadratic equations and mastering algebraic manipulation. By the end, you'll not only understand how to approach this specific problem but also gain a deeper understanding of factorisation techniques applicable to a wider range of quadratic expressions.
Understanding Quadratic Expressions
Before we tackle x² + 4x + 12, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants. Factorisation is the process of expressing a quadratic expression as a product of two or more simpler expressions. This process is fundamental in solving quadratic equations and simplifying algebraic expressions.
Attempting to Factorise x² + 4x + 12 using Traditional Methods
The most common method for factorising quadratic expressions of the form ax² + bx + c is to find two numbers that add up to 'b' and multiply to 'ac'. In our case, a = 1, b = 4, and c = 12. We need to find two numbers that add up to 4 and multiply to 12.
Let's try some possibilities:
- 2 and 6: 2 + 6 = 8 (incorrect)
- 3 and 4: 3 + 4 = 7 (incorrect)
- 1 and 12: 1 + 12 = 13 (incorrect)
None of these pairs satisfy both conditions. This indicates that the quadratic expression x² + 4x + 12 cannot be factorised using integers. This doesn't mean it's unfactorisable; it simply means the factors won't be simple whole numbers.
Exploring Other Factorisation Techniques
Since the traditional method fails, we need to explore alternative approaches. These include:
-
Completing the Square: This method involves manipulating the expression to create a perfect square trinomial. While it can always be used to factorise a quadratic, it can be more complex than other methods.
-
Quadratic Formula: The quadratic formula is a powerful tool that provides the roots (solutions) of any quadratic equation. These roots can then be used to construct the factors.
-
Using Complex Numbers: Because the expression doesn't factorise neatly using real numbers, we might need to use complex numbers to find its factors.
Completing the Square for x² + 4x + 12
Let's try completing the square:
-
Isolate the x terms: We start with x² + 4x + 12. We want to manipulate the x² and 4x terms to form a perfect square.
-
Find the term to complete the square: To complete the square for x² + 4x, we take half of the coefficient of x (which is 4/2 = 2) and square it (2² = 4).
-
Rewrite the expression: We rewrite the expression as (x² + 4x + 4) + 8. Notice that we've added and subtracted 4 to maintain the original value of the expression.
-
Factor the perfect square trinomial: (x² + 4x + 4) is a perfect square trinomial, which factors to (x + 2)².
-
Final form: The expression becomes (x + 2)² + 8. This is the completed square form. This shows that the expression doesn't factorise into two linear expressions with real coefficients.
Applying the Quadratic Formula
The quadratic formula is a powerful tool that solves quadratic equations of the form ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our expression, a = 1, b = 4, and c = 12. Plugging these values into the formula, we get:
x = [-4 ± √(4² - 4 * 1 * 12)] / 2 * 1 x = [-4 ± √(16 - 48)] / 2 x = [-4 ± √(-32)] / 2
Notice the presence of a negative number under the square root. This indicates that the roots of the equation x² + 4x + 12 = 0 are complex numbers.
Understanding Complex Numbers
Complex numbers are numbers that can be expressed in the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit, defined as √(-1). In our case, √(-32) can be simplified to √(32) * i = 4√2 * i.
Therefore, the roots are:
x = [-4 + 4√2i] / 2 = -2 + 2√2i x = [-4 - 4√2i] / 2 = -2 - 2√2i
Factoring using Complex Roots
Knowing the roots, we can factorise the quadratic expression using the following relationship:
If r₁ and r₂ are the roots of a quadratic equation, then the quadratic expression can be factored as a(x - r₁)(x - r₂), where 'a' is the coefficient of x².
In our case, a = 1, r₁ = -2 + 2√2i, and r₂ = -2 - 2√2i. Therefore, the factorised form is:
(x - (-2 + 2√2i))(x - (-2 - 2√2i)) = (x + 2 - 2√2i)(x + 2 + 2√2i)
Why the Initial Approach Failed
The initial attempt to factorise x² + 4x + 12 using integers failed because the expression has no real linear factors. The roots of the corresponding quadratic equation are complex numbers, indicating that the factors involve the imaginary unit 'i'.
Frequently Asked Questions (FAQ)
-
Q: Can all quadratic expressions be factorised? A: Yes, all quadratic expressions can be factorised, but the factors may involve complex numbers, as demonstrated in this example.
-
Q: What is the significance of the discriminant (b² - 4ac)? A: The discriminant determines the nature of the roots. If b² - 4ac > 0, the roots are real and distinct. If b² - 4ac = 0, the roots are real and equal. If b² - 4ac < 0, the roots are complex conjugates.
-
Q: Are there other methods to factorise quadratic expressions? A: Yes, methods like the AC method (for expressions where a ≠ 1) and graphical methods can also be used.
-
Q: Why is factorisation important? A: Factorisation is crucial for solving quadratic equations, simplifying algebraic expressions, and understanding the behaviour of quadratic functions.
Conclusion
While the quadratic expression x² + 4x + 12 cannot be factorised using only integers, it can be factorised using complex numbers. This example highlights the importance of understanding different factorisation techniques and the nature of complex numbers in solving quadratic equations. The process of completing the square and utilising the quadratic formula are powerful tools in cases where simple integer factoring fails. The key takeaway is that even seemingly unfactorisable expressions can be expressed as a product of simpler terms by employing appropriate mathematical methods, showcasing the elegance and versatility of algebra. Remember that the presence of a negative discriminant indicates complex roots, leading to factors involving imaginary numbers. This comprehensive exploration should provide a solid understanding of factoring quadratic expressions, regardless of the nature of their roots.
Latest Posts
Latest Posts
-
Industrialization Influences Rates Of Literacy
Sep 11, 2025
-
Blue Gray Text 2 Excel
Sep 11, 2025
-
What Is 30 Off 60
Sep 11, 2025
-
1935 Two Dollar Bill Worth
Sep 11, 2025
-
0 75 As A Whole Number
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Factorise X 2 4x 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.