Find The Sum 6/x-4 5/x
cibeltiagestion
Sep 12, 2025 · 4 min read
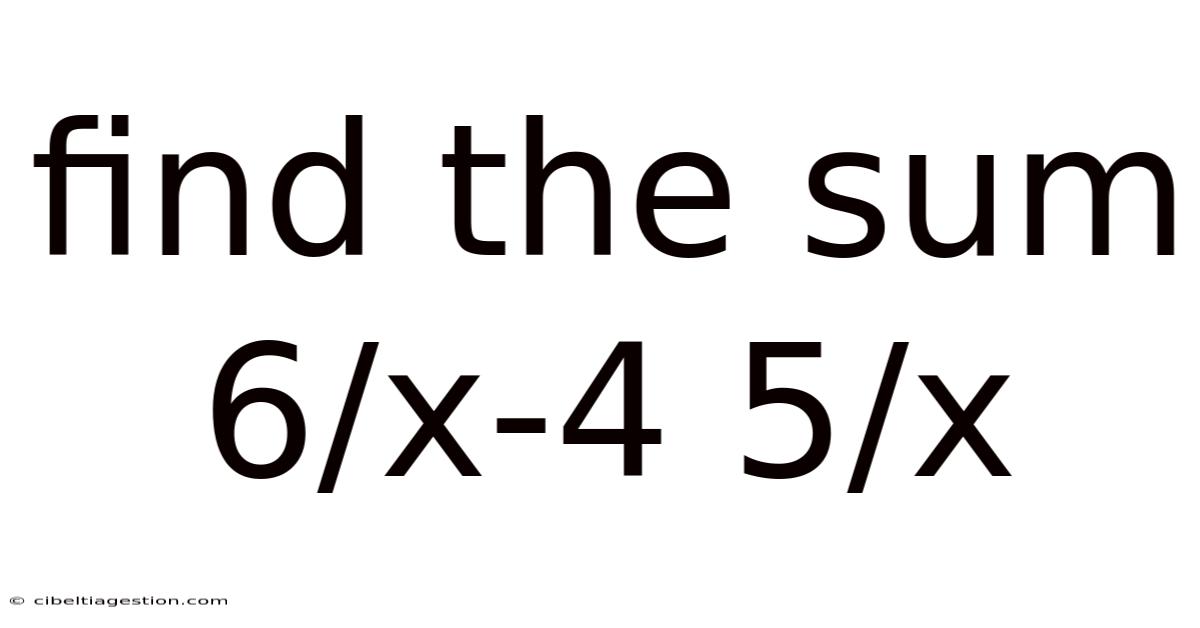
Table of Contents
Finding the Sum of 6/(x-4) and 5/x: A Comprehensive Guide
Finding the sum of two fractions, especially algebraic fractions like 6/(x-4) and 5/x, requires understanding fundamental principles of algebra and fraction manipulation. This comprehensive guide will walk you through the process step-by-step, explaining the underlying concepts and addressing common questions. We'll cover the method, explain the underlying mathematical principles, and provide practice problems to solidify your understanding. This guide is suitable for students learning algebra and anyone looking to refresh their knowledge of fraction addition.
Introduction: Understanding the Problem
The problem asks us to find the sum of the two algebraic fractions: 6/(x-4) and 5/x. This means we need to find a single fraction that represents the combined value of these two expressions. The key to solving this lies in finding a common denominator. Let's dive into the steps.
Step-by-Step Solution: Finding the Common Denominator
-
Identify the Denominators: Our denominators are (x-4) and x.
-
Find the Least Common Denominator (LCD): The least common denominator is the smallest expression that both denominators divide into evenly. In this case, since (x-4) and x are distinct expressions, the LCD is simply their product: x(x-4).
-
Rewrite the Fractions with the LCD: We need to rewrite each fraction so that it has the LCD, x(x-4), as its denominator. To do this, we multiply the numerator and denominator of each fraction by the appropriate factor.
-
For 6/(x-4), we multiply the numerator and denominator by x: [6x]/[x(x-4)]
-
For 5/x, we multiply the numerator and denominator by (x-4): [5(x-4)]/[x(x-4)]
-
-
Add the Fractions: Now that both fractions have the same denominator, we can add their numerators:
[6x]/[x(x-4)] + [5(x-4)]/[x(x-4)] = [6x + 5(x-4)]/[x(x-4)]
-
Simplify the Numerator: Expand and simplify the numerator:
[6x + 5x - 20]/[x(x-4)] = [11x - 20]/[x(x-4)]
Therefore, the sum of 6/(x-4) and 5/x is (11x - 20)/[x(x-4)].
Mathematical Principles: A Deeper Dive
The process of adding fractions relies on several key mathematical concepts:
-
Equivalent Fractions: Multiplying the numerator and denominator of a fraction by the same non-zero number results in an equivalent fraction. This is a fundamental property of fractions and allows us to rewrite fractions with a common denominator.
-
Least Common Multiple (LCM): Finding the least common denominator is essentially finding the least common multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators. In the case of algebraic expressions, we find the least common multiple by considering the factors of each expression.
-
Distributive Property: When simplifying the numerator, we used the distributive property: a(b + c) = ab + ac. This property allows us to expand expressions like 5(x-4) to 5x - 20.
-
Simplifying Algebraic Fractions: The final answer, (11x - 20)/[x(x-4)], is a simplified algebraic fraction. We cannot further simplify this expression unless we know a specific value for x. However, we can note that the expression is undefined when x = 0 or x = 4 because these values would make the denominator zero, resulting in division by zero which is undefined in mathematics.
Practice Problems
To strengthen your understanding, try solving these similar problems:
-
Find the sum of 2/(x+1) and 3/x.
-
Find the sum of 4/(x-2) and 1/(2x).
-
Find the sum of (x+1)/(x-3) and (x-2)/x.
Solutions to Practice Problems:
-
2/(x+1) + 3/x = [2x + 3(x+1)]/[x(x+1)] = (5x + 3)/[x(x+1)]
-
4/(x-2) + 1/(2x) = [8x + (x-2)]/[2x(x-2)] = (9x - 2)/[2x(x-2)]
-
(x+1)/(x-3) + (x-2)/x = [x(x+1) + (x-2)(x-3)]/[x(x-3)] = (x² + x + x² - 5x + 6)/[x(x-3)] = (2x² - 4x + 6)/[x(x-3)]
Frequently Asked Questions (FAQ)
-
What if the denominators have common factors? If the denominators share common factors, you can simplify the process by finding the least common denominator instead of simply multiplying the denominators. This makes simplification easier.
-
Can I always simplify the resulting fraction? Not necessarily. The simplified fraction (11x - 20)/[x(x-4)] cannot be simplified further unless you have a specific value for x. Always check for common factors in the numerator and denominator after simplifying.
-
What happens if the denominator is zero? The expression becomes undefined. This is because division by zero is not allowed in mathematics. You must specify restrictions on the value of x to avoid division by zero. In our original problem, x cannot be 0 or 4.
Conclusion: Mastering Fraction Addition
Adding algebraic fractions like 6/(x-4) and 5/x requires a systematic approach. By finding the least common denominator, rewriting the fractions with this common denominator, adding the numerators, and simplifying the resulting expression, you can successfully find the sum. Remember to always check for restrictions on the variable to avoid division by zero. Mastering this skill is crucial for further studies in algebra and calculus. Practice consistently to build your confidence and proficiency in handling algebraic fractions. The more you practice, the easier it will become!
Latest Posts
Latest Posts
-
3 10 15 Minus 1 12 15
Sep 12, 2025
-
How Tall Is 181 Cm
Sep 12, 2025
-
Chemical Reaction Formula For Photosynthesis
Sep 12, 2025
-
8 Milliliters To Fluid Ounces
Sep 12, 2025
-
Most Minor Violations Will Drop
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Find The Sum 6/x-4 5/x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.