Gcf Of 16 And 28
cibeltiagestion
Sep 10, 2025 · 6 min read
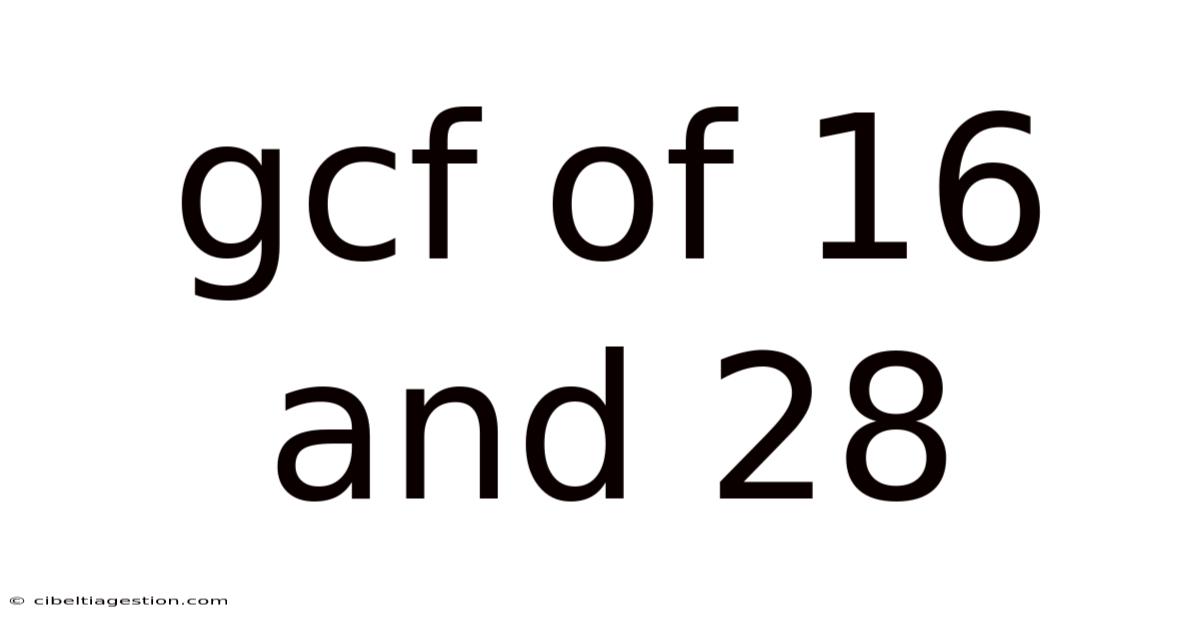
Table of Contents
Finding the Greatest Common Factor (GCF) of 16 and 28: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will explore various methods to determine the GCF of 16 and 28, providing a detailed explanation suitable for students of all levels. We will delve into the process, exploring different techniques and illustrating their application with clear examples. Understanding GCFs is crucial for simplifying fractions, solving algebraic equations, and building a stronger foundation in arithmetic and algebra.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all the given numbers without leaving a remainder. In simpler terms, it's the biggest number that can be divided into each number perfectly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Finding the GCF is a key skill in simplifying fractions and solving various mathematical problems.
Method 1: Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor. Let's apply this to find the GCF of 16 and 28.
Factors of 16: 1, 2, 4, 8, 16 Factors of 28: 1, 2, 4, 7, 14, 28
By comparing the lists, we can see the common factors are 1, 2, and 4. The largest of these common factors is 4. Therefore, the GCF of 16 and 28 is 4.
This method is straightforward for smaller numbers, but it becomes less efficient as the numbers increase in size.
Method 2: Prime Factorization
Prime factorization is a more efficient method for finding the GCF, especially when dealing with larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.).
Let's find the prime factorization of 16 and 28:
Prime factorization of 16: 2 x 2 x 2 x 2 = 2<sup>4</sup> Prime factorization of 28: 2 x 2 x 7 = 2<sup>2</sup> x 7
To find the GCF using prime factorization, we identify the common prime factors and take the lowest power of each. In this case, the only common prime factor is 2, and the lowest power of 2 present in both factorizations is 2<sup>2</sup> (which equals 4). Therefore, the GCF of 16 and 28 is 4.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 16 and 28:
- Start with the larger number (28) and the smaller number (16).
- Divide the larger number by the smaller number and find the remainder: 28 ÷ 16 = 1 with a remainder of 12.
- Replace the larger number with the smaller number (16) and the smaller number with the remainder (12).
- Repeat the process: 16 ÷ 12 = 1 with a remainder of 4.
- Repeat again: 12 ÷ 4 = 3 with a remainder of 0.
- The last non-zero remainder is the GCF. In this case, the GCF is 4.
Illustrative Examples: Applying GCF Concepts
Understanding the GCF has practical applications in various mathematical contexts. Let's explore a few examples:
Example 1: Simplifying Fractions:
Consider the fraction 16/28. To simplify this fraction to its lowest terms, we find the GCF of 16 and 28, which is 4. We then divide both the numerator and the denominator by the GCF:
16 ÷ 4 = 4 28 ÷ 4 = 7
Therefore, the simplified fraction is 4/7.
Example 2: Solving Word Problems:
Suppose you have 16 apples and 28 oranges. You want to divide both fruits into bags such that each bag contains the same number of apples and oranges, and no fruit is left over. The maximum number of bags you can create is determined by the GCF of 16 and 28. Since the GCF is 4, you can create 4 bags, with each bag containing 4 apples and 7 oranges.
Example 3: Area and Perimeter Problems:
Imagine a rectangular garden with an area of 16 square meters and a perimeter of 28 meters. Finding the GCF can help analyze the possible dimensions of the garden.
Beyond the Basics: Extending GCF Concepts
The concept of GCF extends beyond just two numbers. We can find the GCF of three or more numbers using the same methods, particularly the prime factorization method or the Euclidean algorithm (which can be extended to more than two numbers). For instance, to find the GCF of 16, 28, and 36:
- Prime factorization:
- 16 = 2<sup>4</sup>
- 28 = 2<sup>2</sup> x 7
- 36 = 2<sup>2</sup> x 3<sup>2</sup>
The common prime factor is 2, and the lowest power is 2<sup>2</sup> = 4. Therefore, the GCF of 16, 28, and 36 is 4.
- Euclidean Algorithm (extended): This would require multiple steps, repeatedly finding remainders and reducing the numbers until a common GCF emerges.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. This means they share no common factors other than 1.
Q: Are there any shortcuts for finding the GCF?
A: For small numbers, visual inspection of factors can be quick. However, for larger numbers, the prime factorization method and Euclidean algorithm are significantly more efficient.
Q: Can I use a calculator to find the GCF?
A: Many calculators and online tools have built-in functions to calculate the GCF. However, understanding the underlying methods is crucial for a deeper mathematical understanding.
Q: Why is finding the GCF important?
A: Finding the GCF is crucial for simplifying fractions, solving problems involving ratios and proportions, understanding divisibility rules, and laying a strong foundation for more advanced mathematical concepts.
Conclusion
Finding the greatest common factor (GCF) of 16 and 28, as demonstrated in this article, illustrates a fundamental concept in mathematics with broad applications. The three methods—listing factors, prime factorization, and the Euclidean algorithm—each offer unique approaches to solving this problem, with the latter two being particularly efficient for larger numbers. Mastering these techniques provides a crucial building block for further mathematical exploration and problem-solving. Remember, understanding the why behind the methods is just as important as knowing how to apply them. This comprehensive understanding not only enhances your mathematical skills but also empowers you to tackle more complex mathematical challenges with confidence.
Latest Posts
Latest Posts
-
Relationship Building At Work Can
Sep 10, 2025
-
White Lettering And Symbols Painted
Sep 10, 2025
-
Never Let Monkeys Eat Bananas
Sep 10, 2025
-
Dollar General Safety Orientation Answers
Sep 10, 2025
-
Look At The Protein Below
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 16 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.