Graph Y 1 2x 2
cibeltiagestion
Sep 12, 2025 · 6 min read
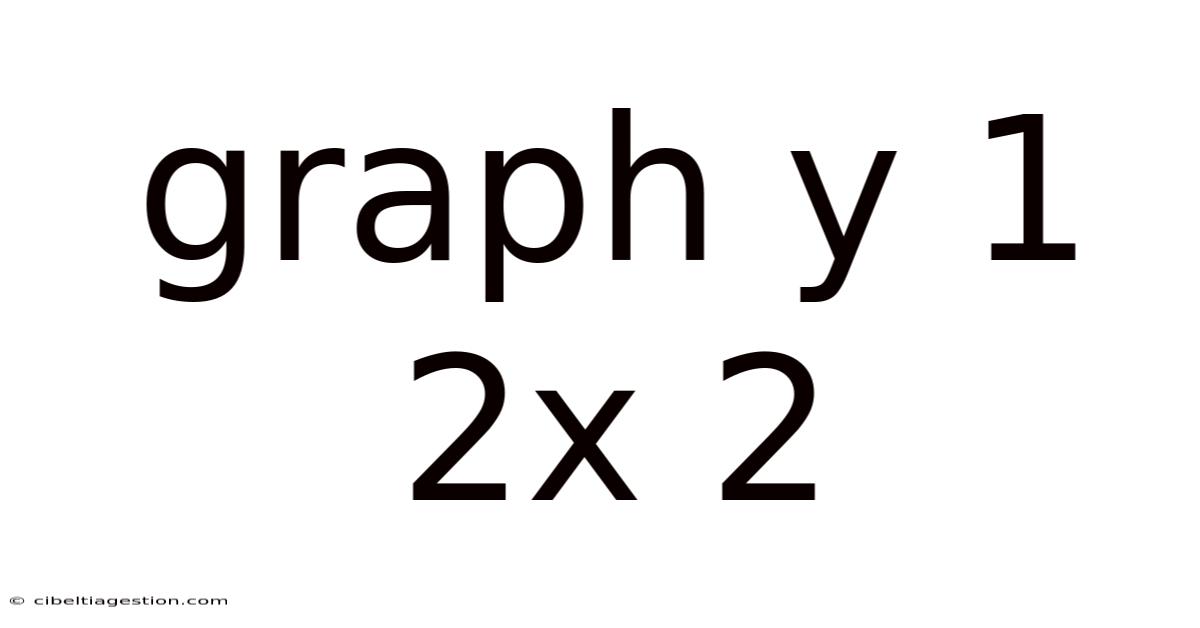
Table of Contents
Unveiling the Secrets of the Graph y = 1/(2x + 2): A Comprehensive Guide
The equation y = 1/(2x + 2) represents a fascinating example of a rational function. Understanding its graph requires a deep dive into its key features, including asymptotes, intercepts, domain, and range. This comprehensive guide will walk you through every aspect of this function, equipping you with the knowledge to confidently analyze and interpret its graphical representation. We'll explore its behavior, delve into the underlying mathematical principles, and address frequently asked questions. By the end, you'll have a solid understanding of this seemingly simple yet surprisingly rich equation.
Introduction: What is a Rational Function?
Before we delve into the specifics of y = 1/(2x + 2), let's establish a foundational understanding of rational functions. A rational function is defined as the ratio of two polynomial functions, where the denominator is not a zero polynomial. In simpler terms, it's a fraction where both the numerator and denominator are polynomials. Our equation, y = 1/(2x + 2), perfectly fits this definition: the numerator is the constant polynomial 1, and the denominator is the linear polynomial 2x + 2.
Understanding rational functions is crucial in various fields, including calculus, physics, and engineering. They often model real-world phenomena involving rates, ratios, and inverse relationships.
Analyzing the Key Features of y = 1/(2x + 2)
To fully grasp the graph of y = 1/(2x + 2), we must systematically analyze its key features:
1. Domain and Range
The domain of a function represents all possible input values (x-values) for which the function is defined. In our case, the function is undefined when the denominator is zero. Therefore, we set the denominator equal to zero and solve for x:
2x + 2 = 0 2x = -2 x = -1
This means the function is undefined at x = -1. The domain is all real numbers except x = -1, which can be expressed in interval notation as (-∞, -1) U (-1, ∞).
The range of a function represents all possible output values (y-values). Since the numerator is a constant (1) and the denominator can take on any value except 0, y can take on any value except 0. Therefore, the range is (-∞, 0) U (0, ∞).
2. Asymptotes
Asymptotes are lines that the graph of a function approaches but never touches. Rational functions often have vertical and horizontal asymptotes.
-
Vertical Asymptote: A vertical asymptote occurs at the x-value where the denominator is zero and the numerator is non-zero. In our case, we already identified this as x = -1. Therefore, the vertical asymptote is the line x = -1.
-
Horizontal Asymptote: A horizontal asymptote describes the behavior of the function as x approaches positive or negative infinity. To find the horizontal asymptote, we examine the degrees of the numerator and denominator polynomials. Since the degree of the numerator (0) is less than the degree of the denominator (1), the horizontal asymptote is y = 0.
3. Intercepts
-
x-intercept: The x-intercept is the point where the graph intersects the x-axis (where y = 0). Since the numerator is always 1, the function will never equal zero. Therefore, there is no x-intercept.
-
y-intercept: The y-intercept is the point where the graph intersects the y-axis (where x = 0). To find this, we substitute x = 0 into the equation:
y = 1/(2(0) + 2) = 1/2
Therefore, the y-intercept is (0, 1/2).
4. Analyzing the Behavior Around the Asymptotes
Understanding how the function behaves around its asymptotes is crucial for accurate graphing.
-
Near x = -1: As x approaches -1 from the left (x → -1⁻), the denominator (2x + 2) approaches 0 from the negative side. This results in y approaching negative infinity (y → -∞). As x approaches -1 from the right (x → -1⁺), the denominator approaches 0 from the positive side, resulting in y approaching positive infinity (y → ∞).
-
As x approaches ±∞: As x becomes very large (positive or negative), the term 2x in the denominator dominates, and the function approaches y = 0. This confirms our horizontal asymptote.
Step-by-Step Graphing of y = 1/(2x + 2)
Now, let's combine our analysis to construct the graph:
-
Plot the y-intercept: Mark the point (0, 1/2) on your graph.
-
Draw the asymptotes: Draw the vertical line x = -1 and the horizontal line y = 0. These lines will guide the shape of your graph.
-
Sketch the branches: Based on our analysis of the behavior near the asymptotes, sketch the branches of the graph. To the left of x = -1, the graph will approach the vertical asymptote from below (towards -∞), and to the right of x = -1, it will approach from above (towards ∞). As x moves towards positive or negative infinity, the graph will approach the horizontal asymptote y = 0.
Your final graph should show two distinct branches, one in the second quadrant and one in the fourth quadrant, separated by the vertical asymptote at x = -1 and approaching the horizontal asymptote y = 0.
Further Exploration and Extensions
The analysis of y = 1/(2x + 2) provides a solid foundation for understanding more complex rational functions. Here are some avenues for further exploration:
-
Transformations: Consider how changing the coefficients in the equation (e.g., y = a/(bx + c)) affects the graph. How do changes to a, b, and c influence the asymptotes, intercepts, and overall shape?
-
Advanced Calculus: Investigating the first and second derivatives of this function can provide insights into its increasing/decreasing behavior and concavity.
-
Applications: Explore real-world scenarios that can be modeled using rational functions of this form. Examples might include inverse proportionality relationships in physics or economics.
Frequently Asked Questions (FAQ)
Q: Can the graph of y = 1/(2x + 2) ever touch its asymptotes?
A: No. By definition, asymptotes are lines that the graph approaches but never actually touches.
Q: What happens to the graph if the denominator is changed?
A: Changing the denominator will shift the vertical asymptote and potentially change the horizontal asymptote, significantly altering the graph's shape.
Q: How can I use software to verify my graph?
A: Many graphing calculators and software packages (like Desmos or GeoGebra) can be used to plot rational functions. Inputting the equation will allow you to visually confirm your hand-drawn graph.
Q: Are there any other types of asymptotes besides vertical and horizontal?
A: Yes, there are also slant or oblique asymptotes, which occur when the degree of the numerator is exactly one greater than the degree of the denominator. However, our function y = 1/(2x+2) does not have a slant asymptote.
Conclusion: Mastering the Graph of y = 1/(2x + 2)
Understanding the graph of y = 1/(2x + 2) requires a methodical approach that incorporates the analysis of its domain, range, asymptotes, and intercepts. By carefully examining the behavior of the function around its asymptotes and applying the principles of rational functions, we can accurately construct and interpret its graphical representation. This understanding serves as a stepping stone to tackling more complex rational functions and their applications in various fields. Remember to practice graphing similar functions to solidify your understanding and build your confidence in analyzing these important mathematical relationships.
Latest Posts
Latest Posts
-
Given Abcd Solve For X
Sep 12, 2025
-
What Is A Unique Polygon
Sep 12, 2025
-
4x 2x 2 3x 7
Sep 12, 2025
-
Ten Fish In A Tank
Sep 12, 2025
-
Question Mo Select The Mechanism
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Graph Y 1 2x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.